Sas で単純な線形回帰を実行する方法

単純線形回帰は、予測変数と応答変数の関係を理解するために使用できる手法です。

この手法は、データに最もよく「適合」する線を見つけ、次の形式になります。

ŷ = b ₀ + b ₁ x

金：

• ŷ : 推定応答値
• b ₀ : 回帰直線の原点
• b ₁ : 回帰直線の傾き

この方程式は、予測変数と応答変数の関係を理解するのに役立ちます。

次の段階的な例は、SAS で単純な線形回帰を実行する方法を示しています。

ステップ 1: データを作成する

この例では、15 人の学生の合計学習時間数と最終試験の成績を含むデータセットを作成します。

時間を予測変数として、スコアを応答変数として使用して、単純な線形回帰モデルを近似します。

次のコードは、SAS でこのデータセットを作成する方法を示しています。

 /*create dataset*/
data exam_data;
    input hours score;
    datalines ;
1 64
2 66
4 76
5 73
5 74
6 81
6 83
7 82
8 80
10 88
11 84
11 82
12 91
12 93
14 89
;
run ;

/*view dataset*/
proc print data =exam_data;

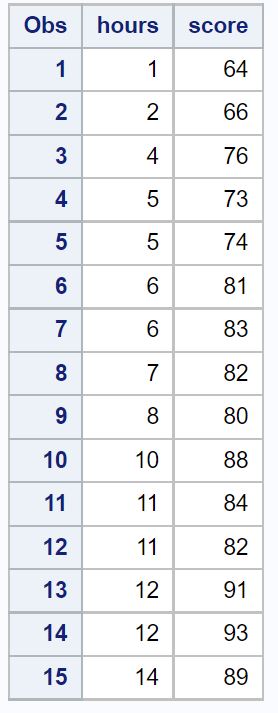
ステップ 2: 単純な線形回帰モデルを当てはめる

次に、 proc reg を使用して単純な線形回帰モデルを当てはめます。

 /*fit simple linear regression model*/
proc reg data =exam_data;
   model score = hours;
run ; 

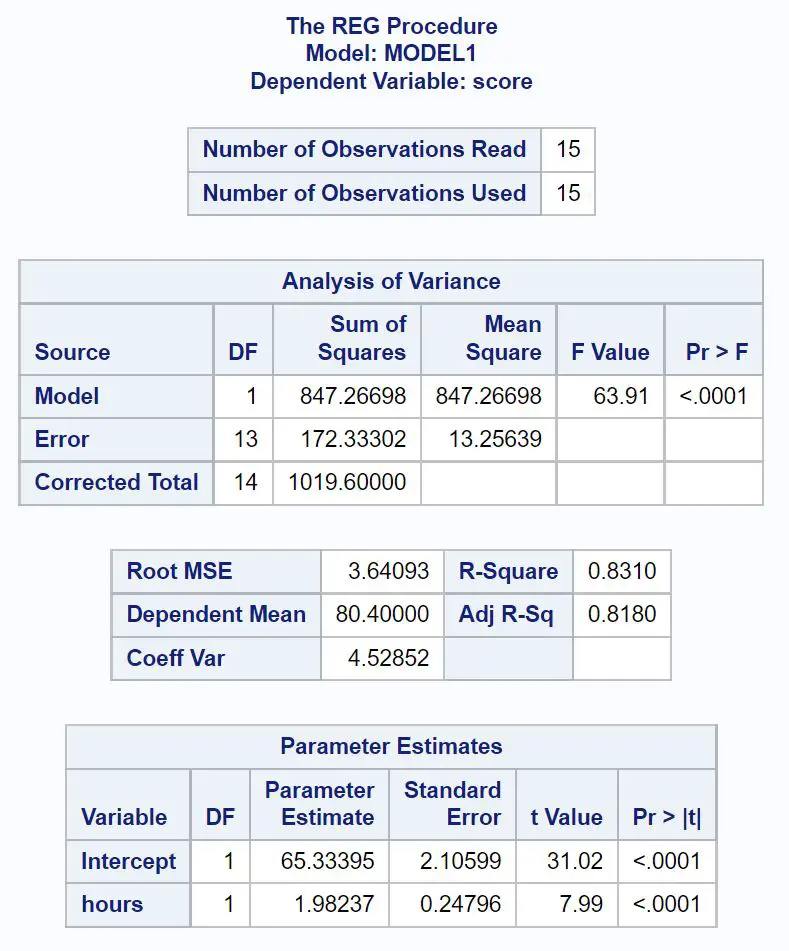
結果の各テーブルから最も重要な値を解釈する方法は次のとおりです。

ギャップ分析テーブル:

回帰モデルの全体的なF 値は63.91で、対応する p 値は< 0.0001です。

この p 値は 0.05 未満であるため、回帰モデル全体が統計的に有意であると結論付けられます。言い換えれば、時間は試験結果を予測するための有用な変数です。

モデル適合表:

R 二乗値は、勉強時間数によって説明できる試験得点の変動のパーセンテージを示します。

一般に、回帰モデルのR 二乗値が大きいほど、予測変数は応答変数の値をより適切に予測します。

この場合、試験の得点の変動の83.1%は勉強時間数で説明できます。この値は非常に高く、勉強時間が試験結果を予測する際に非常に役立つ変数であることを示しています。

パラメータ推定値の表:

この表から、近似された回帰式がわかります。

スコア = 65.33 + 1.98*(時間)

これは、学習時間が追加されるごとに、試験スコアが平均1.98 ポイント増加することを意味すると解釈します。

元の値から、ゼロ時間勉強した生徒の試験の平均点は65.33であることが分かります。

この方程式を使用して、学生の勉強時間に基づいて予想される試験の得点を求めることもできます。

たとえば、10 時間勉強した生徒は、試験スコア85.13を達成する必要があります。

スコア = 65.33 + 1.98*(10) = 85.13

この表では時間のp 値 (<0.0001) が 0.05 未満であるため、これは統計的に有意な予測変数であると結論付けられます。

ステップ 3: 残差プロットを分析する

単純な線形回帰では、モデルの残差について 2 つの重要な仮定が行われます。

• 残差は正規分布します。
• 残差は、予測変数の各レベルで等しい分散 (「等分散性」) を持ちます。

これらの前提が満たされない場合、回帰モデルの結果は信頼できない可能性があります。

これらの仮定が満たされていることを確認するには、SAS が出力に自動的に表示する残差プロットを分析します。

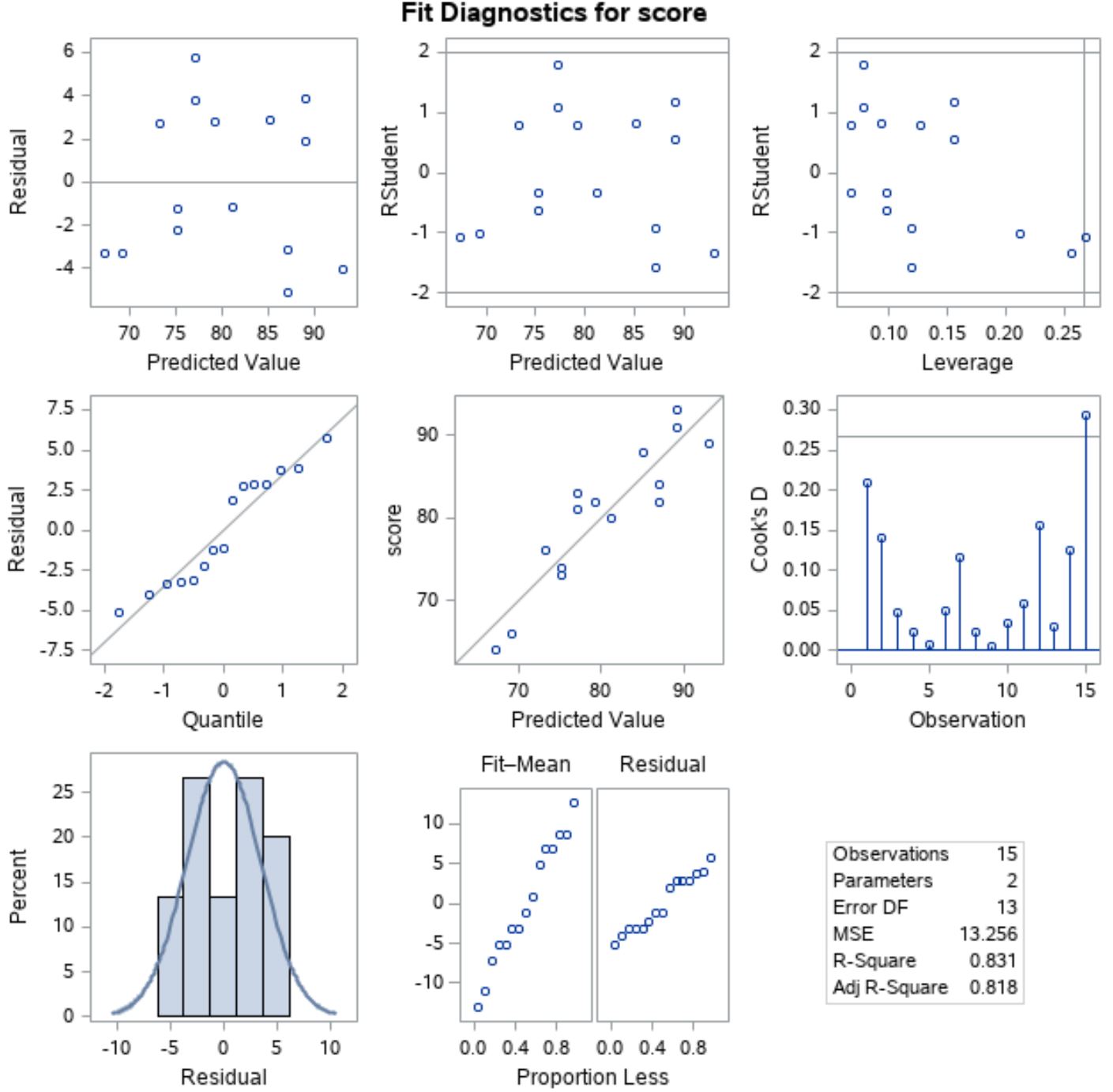
残差が正規分布していることを確認するには、x 軸に沿った「分位数」と y 軸に沿った「残差」を使用して、中央線の左側の位置にあるプロットを分析できます。

このプロットはQQ プロット(「分位数-分位数」の略) と呼ばれ、データが正規分布しているかどうかを判断するために使用されます。データが正規分布している場合、QQ プロット上の点は直線の対角線上にあります。

グラフから、点はほぼ直線の対角線に沿って配置されていることがわかり、残差は正規分布していると仮定できます。

次に、残差が等分散であることを確認するために、最初の行の左側にあるプロットを見て、X 軸に「予測値」、Y 軸に「残差」をとります。

プロット点がゼロの周りにランダムに散在しており、明確なパターンがない場合、残差は等分散であると仮定できます。

プロットから、プロット全体の各レベルでほぼ等しい分散で点がゼロの周りにランダムに散在していることがわかり、残差は等分散であると仮定できます。

両方の仮定が満たされているため、単純な線形回帰モデルの結果は信頼できると仮定できます。

追加リソース

次のチュートリアルでは、SAS で他の一般的なタスクを実行する方法について説明します。

SAS で一元配置分散分析を実行する方法
SAS で二元配置分散分析を実行する方法
SAS で相関関係を計算する方法