シグをどう解釈するか。 spssの値(両面)
SPSS で統計テストを実行すると、出力テーブルにSig が含まれることがよくあります。値(双方向) 。
この値は検定の両側 p 値を表します。
この値が有意水準 (一般的な選択肢は 0.05 または 0.01) を下回る場合、検定の帰無仮説を棄却できます。
このチュートリアルでは、 Sig を解釈する方法の例を示します。さまざまな統計検定の(両側)値。
例 1: 1 サンプルのt 検定
1 サンプル t 検定は、母集団の平均が特定の値に等しいかどうかを検定するために使用されます。
たとえば、植物学者が特定の植物種の平均高さが 15 インチに等しいかどうかを知りたいとします。彼女は 12 本の植物から無作為にサンプルを採取し、それぞれの高さをインチ単位で記録しました。
次に、このサンプルを使用して、次の帰無仮説と対立仮説を使用して 1 サンプルの t 検定を実行します。
- H 0 : μ = 15 (実際の母集団平均は 15 インチに等しい)
- H A : μ ≠ 15 (実際の母集団の平均は 15 インチに等しくない)
彼女は SPSS でこの 1 サンプルの t 検定を実行し、次の結果を得ました。
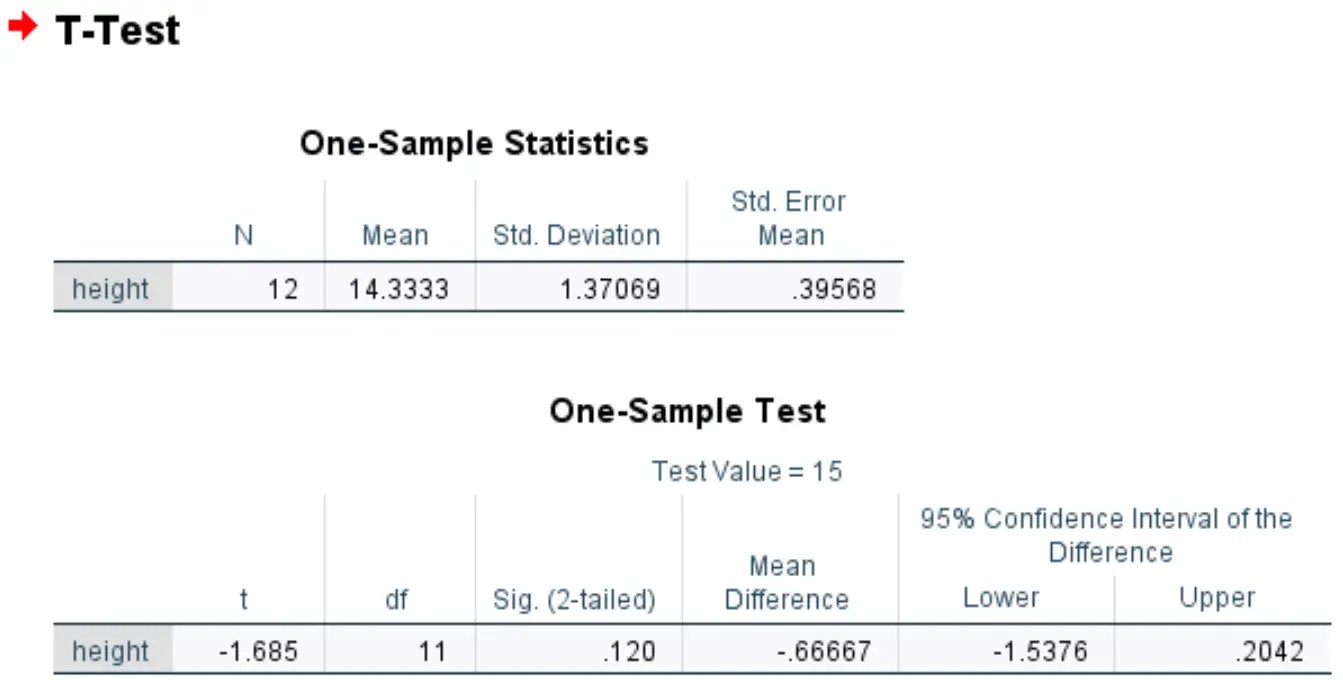
シグ。値 (両側) は0.120です。
これは、11 自由度の値 -1.685 に対応する両側 p 値を表します。
検定の p 値 (0.120) は 0.05 未満ではないため、帰無仮説を棄却できません。
言い換えれば、この植物種の真の平均身長が 15 インチ以外であると言える十分な証拠はありません。
例 2: 2 サンプルのt 検定
2 標本 t 検定は、 2 つの母集団の平均値が等しいかどうかを検定するために使用されます。
たとえば、研究者が、新しい燃料処理によって特定の車の 1 ガロンあたりの平均走行距離に変化が生じるかどうかを知りたいとします。これをテストするために、12 台の車に新しい燃料処理を施し、12 台の車には施さない実験を実施しました。
研究者は、次の帰無仮説と対立仮説を使用して 2 サンプルの t 検定を実行します。
- H 0 : μ 1 = μ 2 (2 つの母集団間の平均 mpg は等しい)
- H 1 : μ 1 ≠ μ 2 (2 つの母集団間の平均 mpg は等しくない)
SPSS で 2 サンプルの t 検定を実行し、次の結果が得られます。
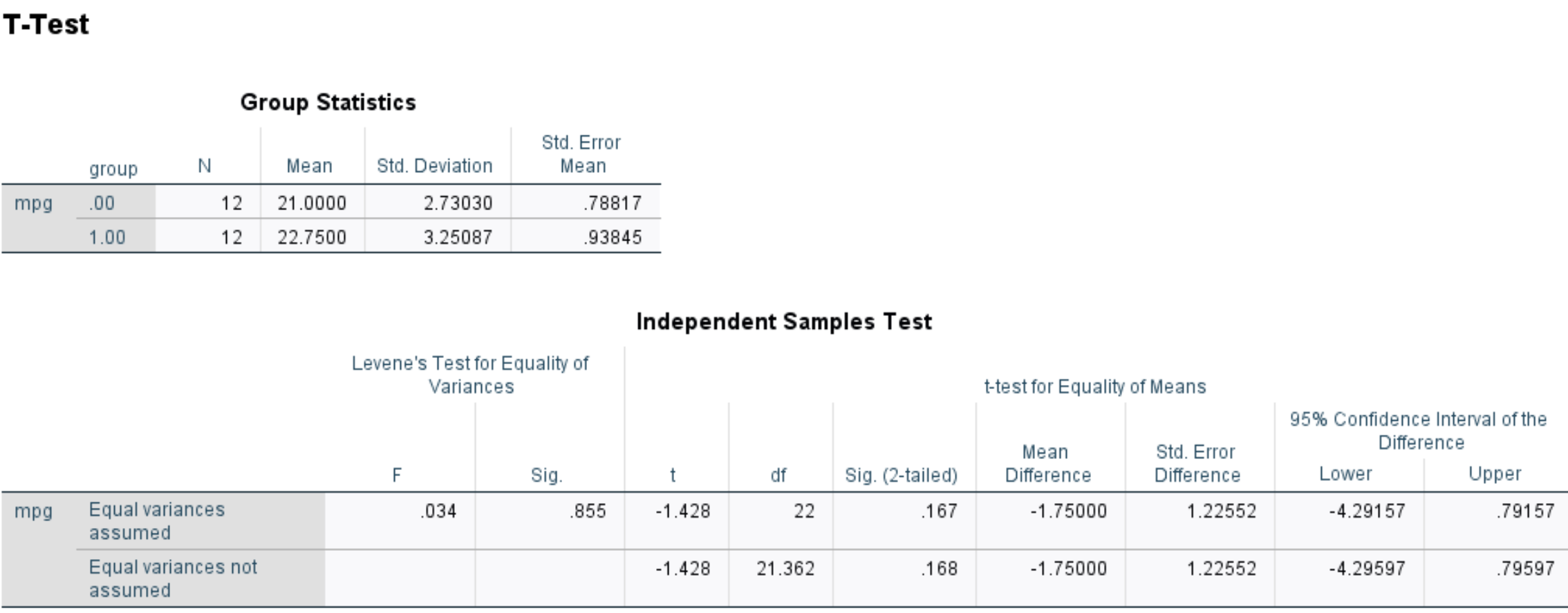
シグ。値 (両側) は0.167です。
これは、22 自由度の値 -1.428 に対応する両側 p 値を表します。
検定の p 値 (0.167) は 0.05 未満ではないため、帰無仮説を棄却できません。
言い換えれば、治療を受けた車と受けていない車の間で真の平均燃費が異なると言える十分な証拠はありません。
追加リソース
次のチュートリアルでは、SPSS でさまざまな統計テストを実行する方法を説明します。
SPSS で 1 サンプルの t 検定を実行する方法
SPSS で 2 サンプルの t 検定を実行する方法
SPSS で対応のあるサンプルの t 検定を実行する方法