Spss で二次回帰を実行する方法

2 つの変数に線形関係がある場合、多くの場合、単純な線形回帰を使用してそれらの関係を定量化できます。

ただし、2 つの変数が非線形の関係にある場合、単純な線形回帰はうまく機能しません。このような場合は、二次回帰を使用してみることができます。

このチュートリアルでは、SPSS で 2 次回帰を実行する方法を説明します。

例: SPSS での二次回帰

労働時間と幸福度の関係を理解したいとします。 16 人の異なる人々の週の労働時間数と報告された幸福度 (0 から 100 のスケール) に関する次のデータがあります。

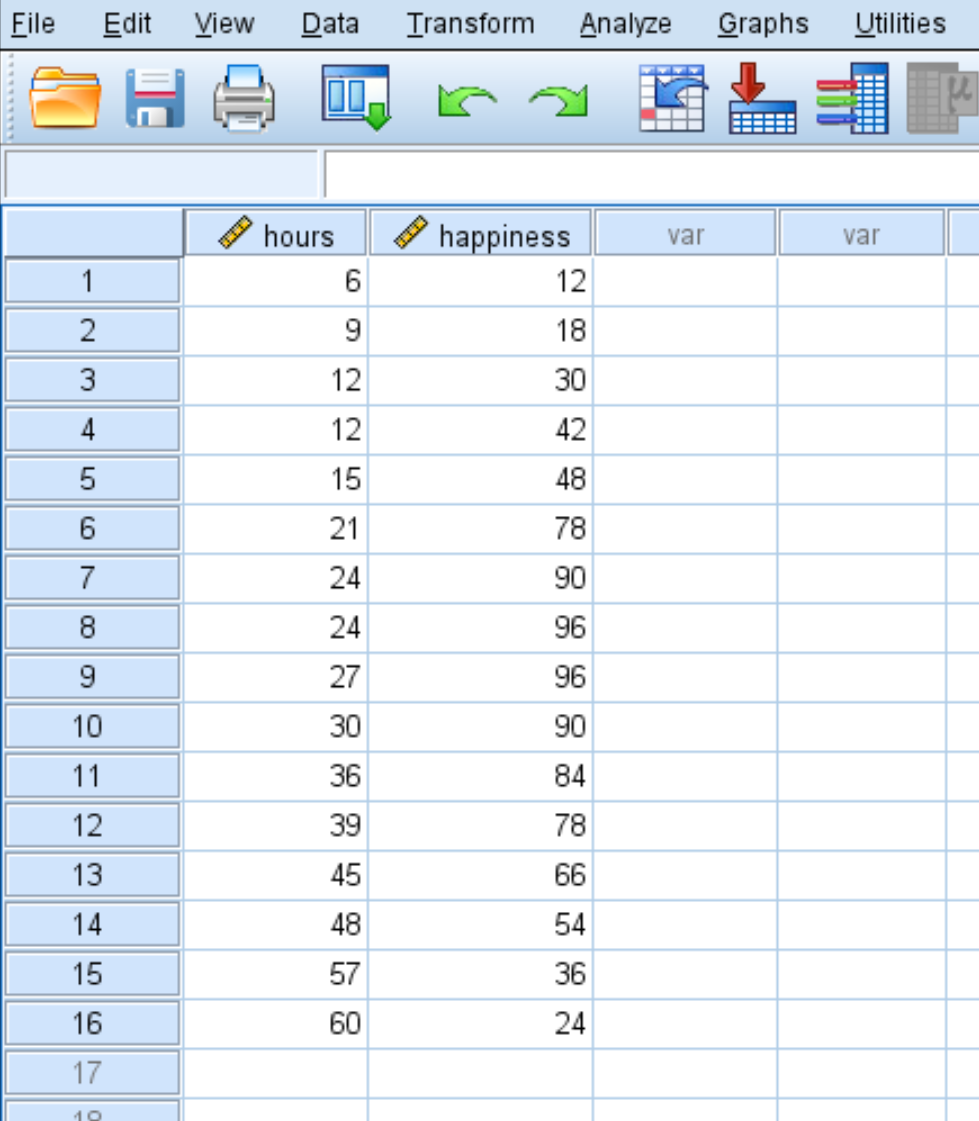
SPSS で 2 次回帰を実行するには、次の手順を使用します。

ステップ 1: データを視覚化します。

二次回帰を実行する前に、散布図を作成して労働時間と幸福度の関係を視覚化し、2 つの変数が実際に二次関係にあることを確認しましょう。

「グラフ」タブをクリックし、 「グラフビルダー」をクリックします。

表示される新しいウィンドウで、 [選択]リストから[散布/ドット]を選択します。次に、 「Simple Scatter」というラベルの付いたチャートをメイン編集ウィンドウにドラッグします。 X 軸の変数時間をドラッグし、Y 軸の幸福度をドラッグします。次に、 「OK」をクリックします。

次の散布図が表示されます。

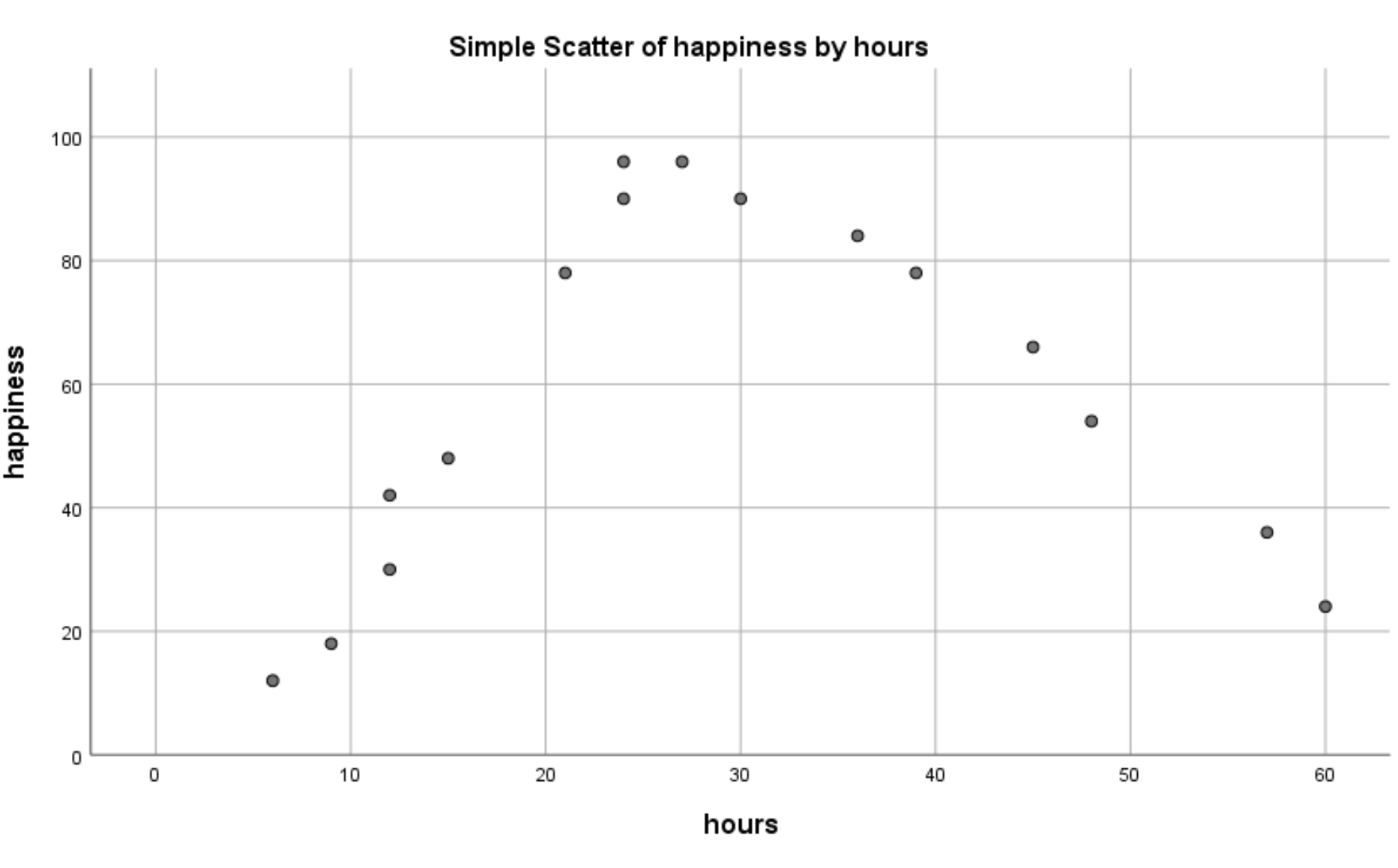
労働時間と幸福の間には非線形の関係があることがはっきりとわかります。これは、二次回帰がこの状況で使用するのに適切な手法であることを示しています。

ステップ 2: 新しい変数を作成します。

二次回帰を実行する前に、時間²の予測子変数を作成する必要があります。

「変換」タブをクリックし、 「変数の計算」をクリックします。

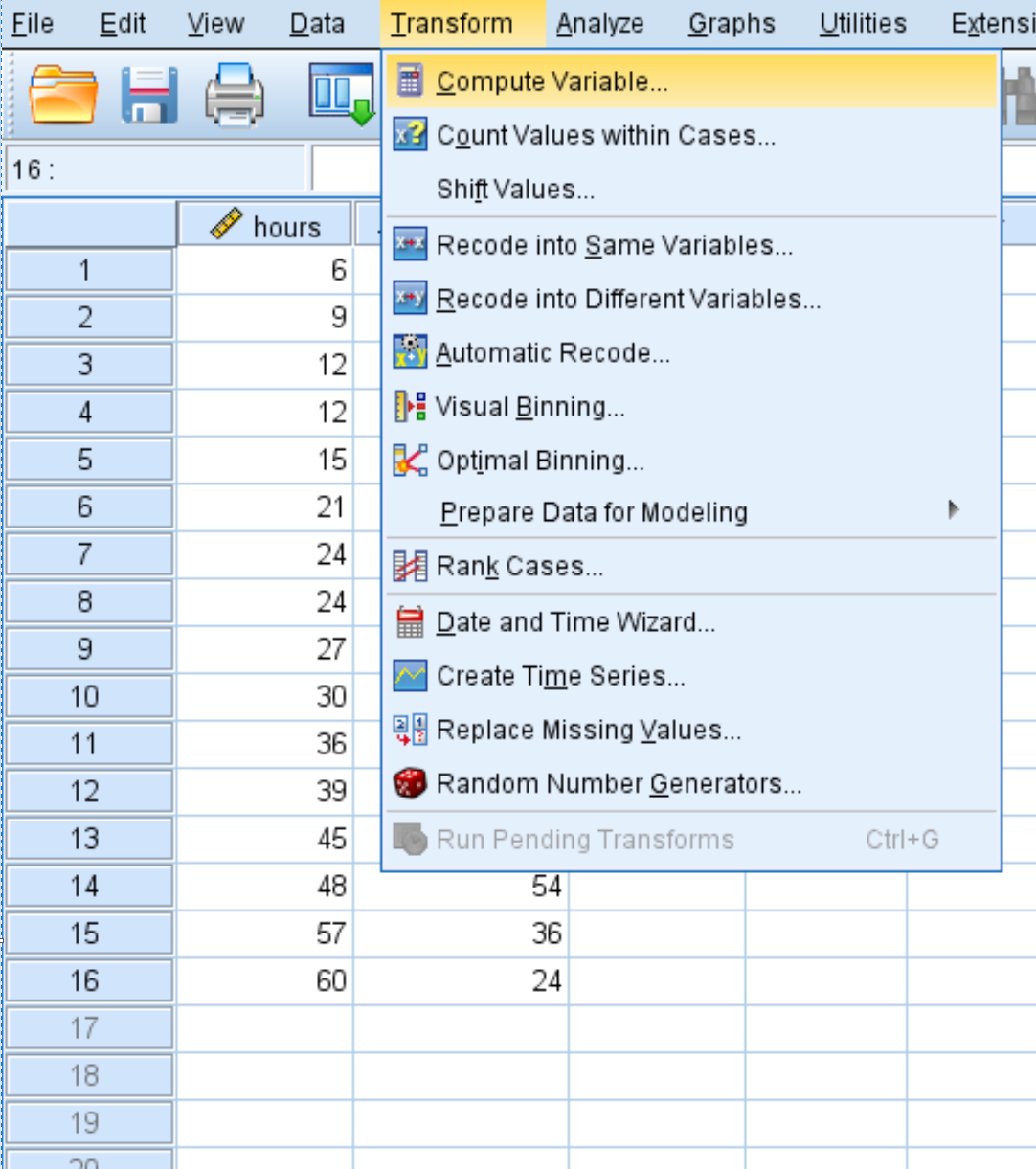
表示される新しいウィンドウで、ターゲット変数にhours2という名前を付け、 hours*hoursに設定します。

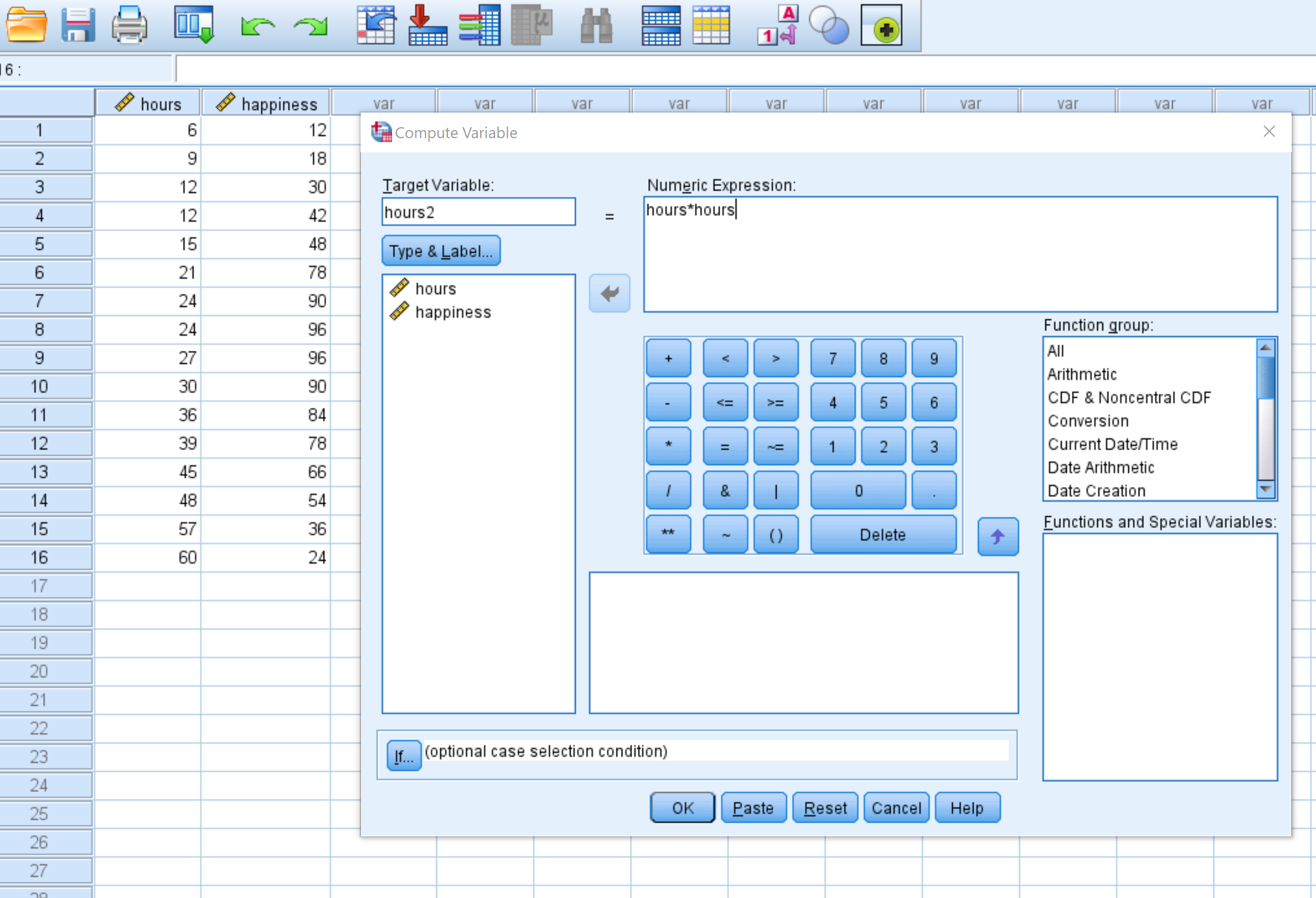
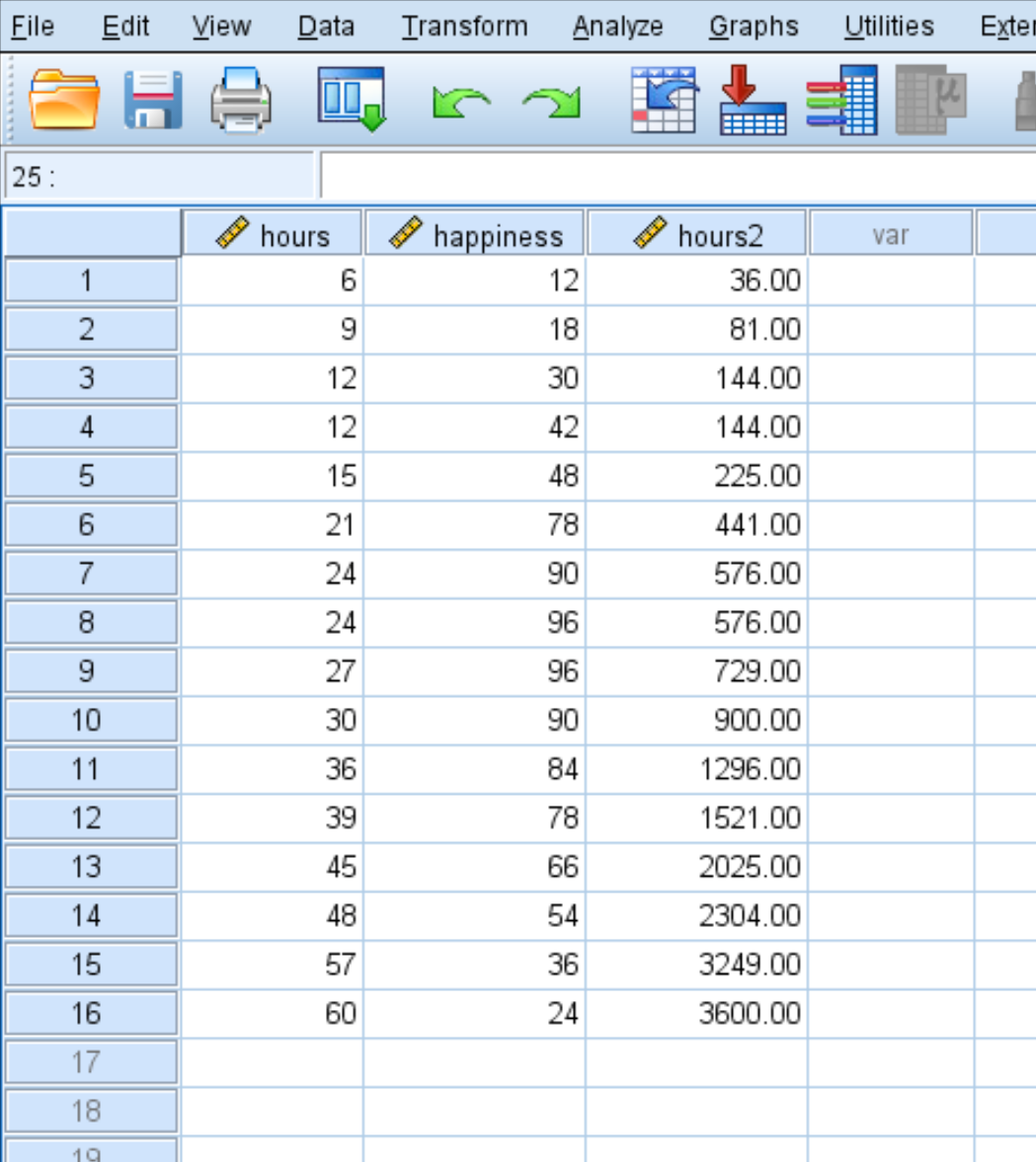
「OK」をクリックすると、 hours2変数が新しい列に表示されます。

ステップ 3: 二次回帰を実行します。

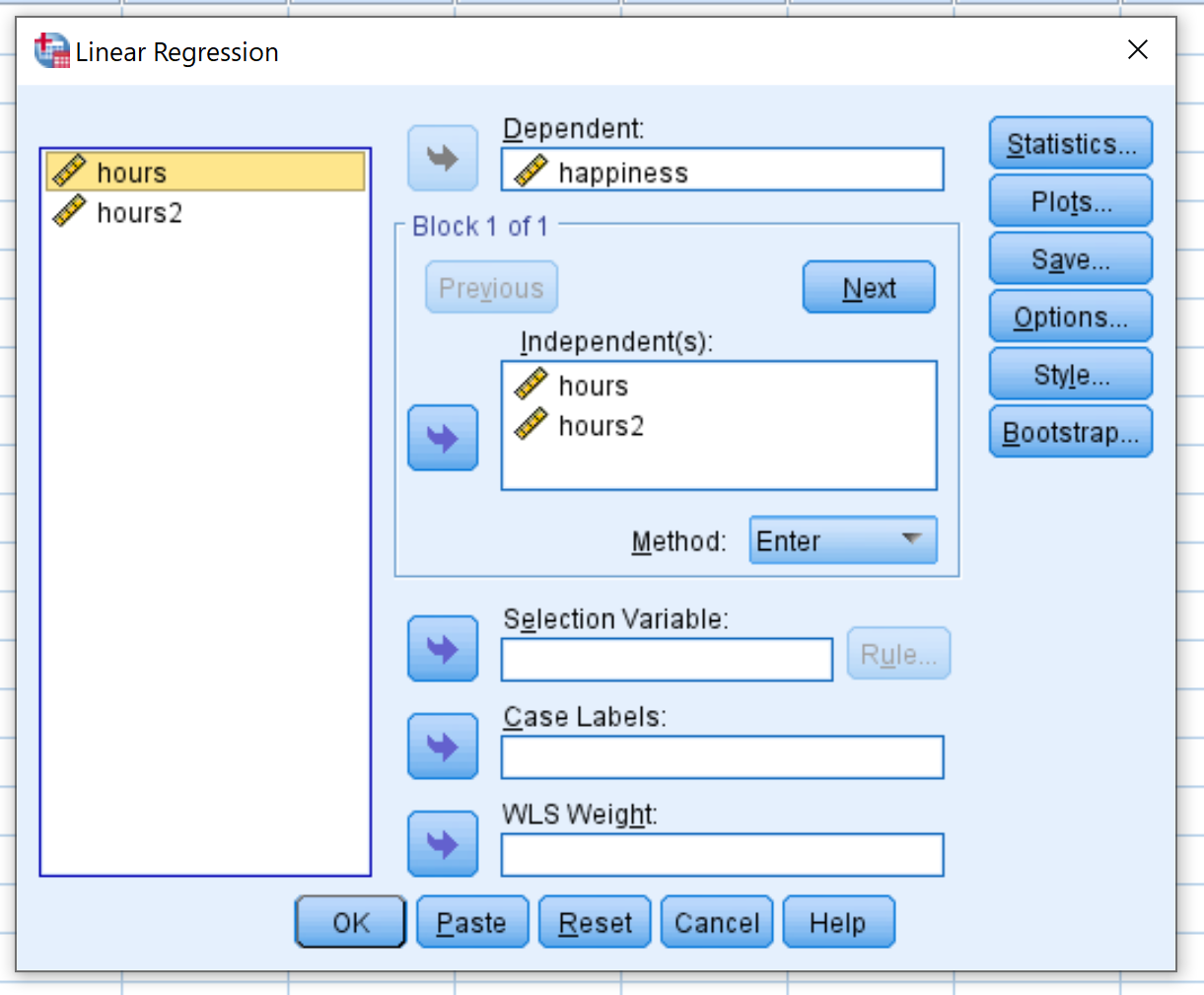
次に、二次回帰を実行します。 「分析」タブ、 「回帰」 、 「線形」の順にクリックします。

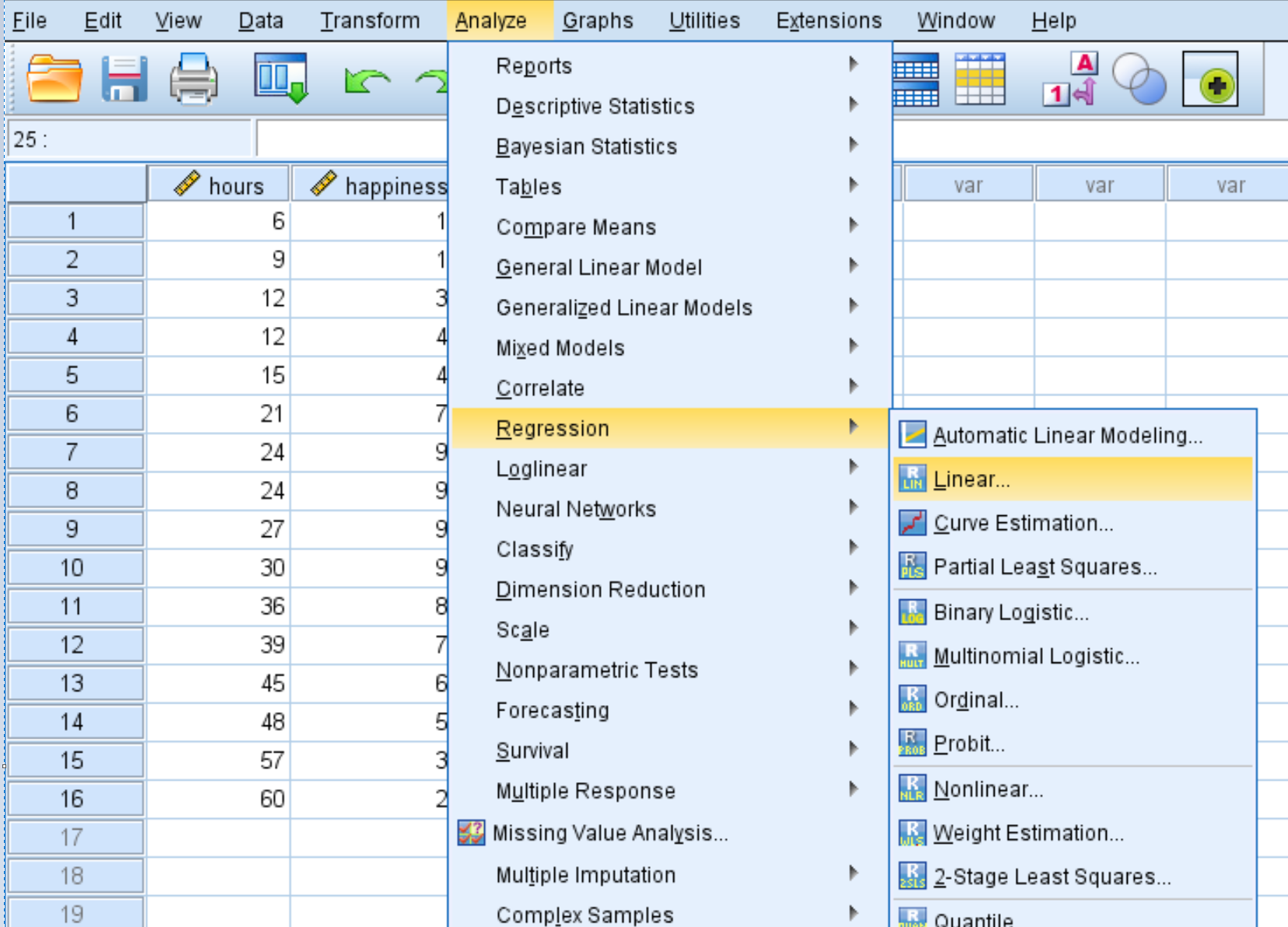
表示される新しいウィンドウで、幸福を「Dependent」というラベルのボックスにドラッグします。 「Hours」と「Hours2」を「Independent(s)」というラベルの付いたボックスにドラッグします。次に、 「OK」をクリックします。

ステップ 4: 結果を解釈します。

[OK]をクリックすると、二次回帰の結果が新しいウィンドウに表示されます。

興味のある最初のテーブルは、 「モデルの概要」と呼ばれます。

この表で最も関連性の高い数値を解釈する方法は次のとおりです。

• R 二乗:これは、説明変数によって説明できる応答変数の分散の割合です。この例では、幸福度の変動の90.9%は、時間と時間^{2 の}変数によって説明できます。
• 標準。推定誤差:標準誤差は、観測値と回帰直線の間の平均距離です。この例では、観測値は回帰直線から平均して9,519単位外れています。

私たちが興味を持っている次のテーブルはANOVAと呼ばれます。

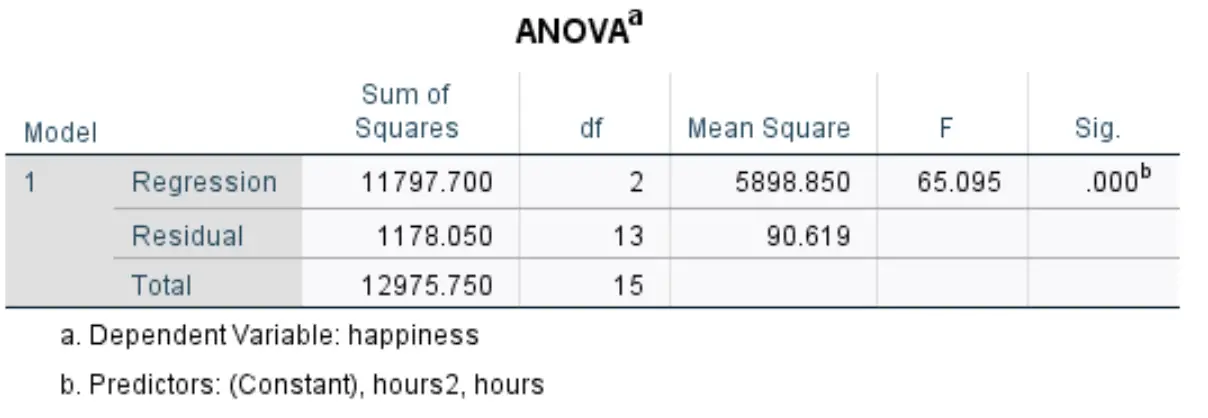
この表で最も関連性の高い数値を解釈する方法は次のとおりです。

• F:これは回帰モデルの全体的な F 統計量であり、平均二乗回帰 / 平均二乗残差として計算されます。
• Sig:これは、全体的な F 統計量に関連付けられた p 値です。これにより、回帰モデル全体が統計的に有意であるかどうかがわかります。この場合、p 値は 0.000 に等しく、説明変数の時間と時間²の組み合わせが検査結果と統計的に有意な関連性があることを示しています。

私たちが興味を持っている次の表には、 「係数」というタイトルが付けられています。

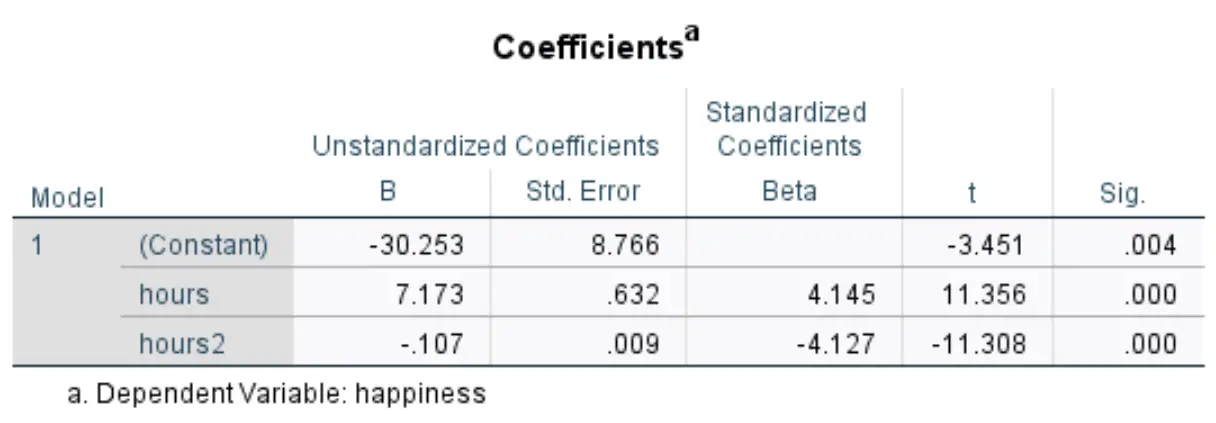
標準化されていない B列の値を使用して、このデータセットの推定回帰式を形成できます。

推定幸福度 = -30.253 + 7.173*(時間) – 0.107*(時間² )

この方程式を使用すると、週あたりの労働時間に基づいて個人の推定幸福度を求めることができます。たとえば、週に 60 時間働く人の幸福度は 14.97 になるはずです。

推定幸福度 = -30.253 + 7.173*(60) – 0.107*(60 ² ) = 14.97 。

逆に、週に 30 時間働く人の幸福度は 88.65 になるはずです。

推定幸福度 = -30.253 + 7.173*(30) – 0.107*(30 ² ) = 88.65 。

ステップ 5: 結果を報告します。

最後に、二次回帰の結果を報告します。これを行う方法の例を次に示します。

個人の労働時間とそれに対応する幸福度 (0 から 100 で測定) との関係を定量化するために、二次回帰が実行されました。分析には16人のサンプルが使用されました。

その結果、説明変数の時間と時間²と応答変数の幸福度の間に統計的に有意な関係があることがわかりました (F(2, 13) = 65.095、p < 0.000)。

これら 2 つの説明変数を合わせると、幸福度の変動の 90.9% が説明されます。

回帰式は次のようになりました。

推定幸福度 = -30.253 + 7.173 (時間) – 0.107 ( ²時間)