Spss で単純な線形回帰を実行する方法
単純線形回帰は、予測変数と応答変数の関係を理解するために使用できる方法です。
このチュートリアルでは、SPSS で単純な線形回帰を実行する方法を説明します。
例: SPSS での単純線形回帰
20 人の学生の学習時間数と試験の成績を示す次のデータセットがあるとします。
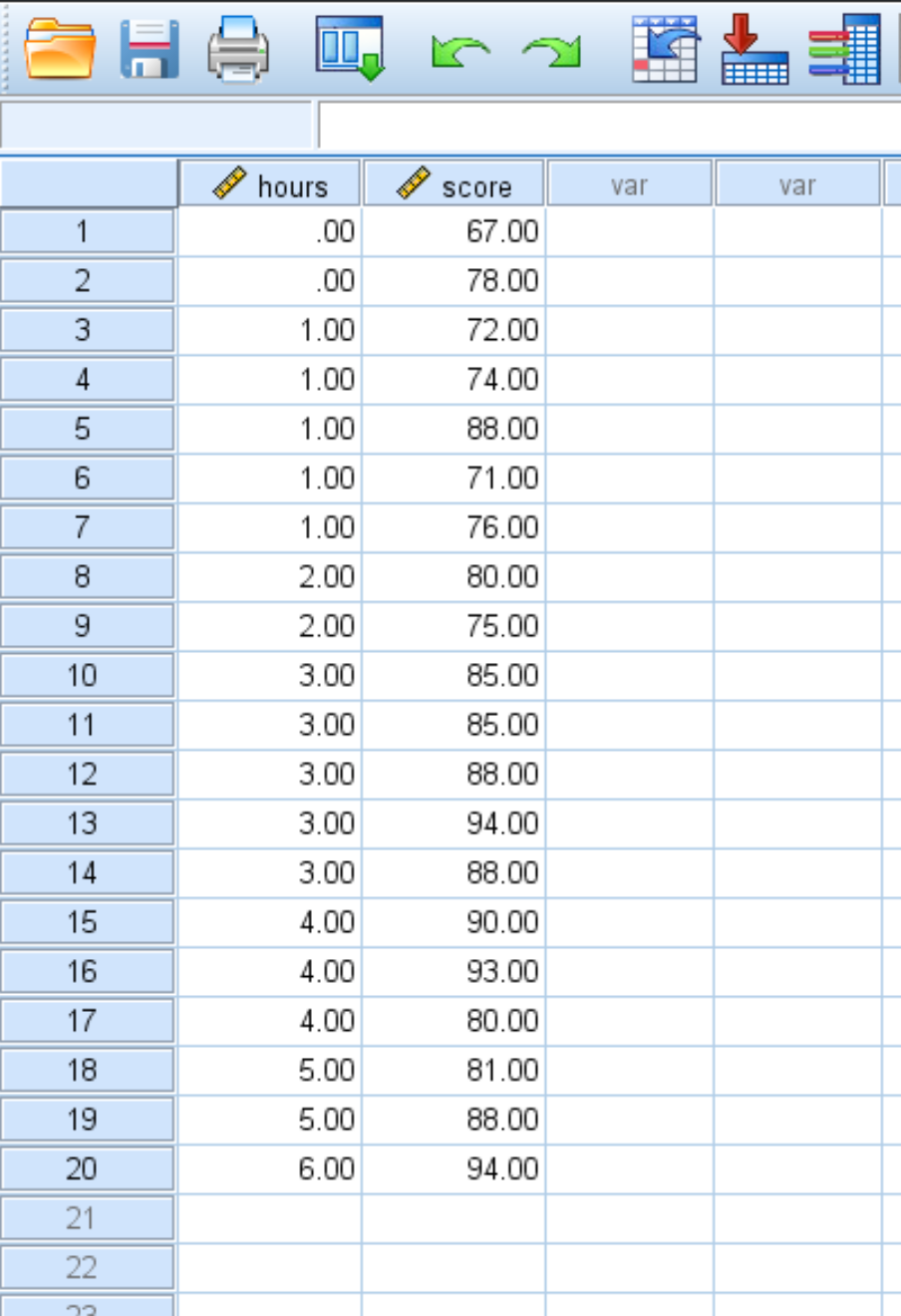
次の手順を使用して、このデータセットに対して単純な線形回帰を実行し、学習時間と試験スコアの関係を定量化します。
ステップ 1: データを視覚化します。
まず、散布図を作成して時間とスコアの関係を視覚化し、2 つの変数間の関係が線形であることを確認します。それ以外の場合、単純な線形回帰は使用する適切な手法ではありません。
「グラフ」タブをクリックし、 「グラフビルダー」をクリックします。
「選択」メニューから「散布/ドット」をクリックしてメイン編集ウィンドウにドラッグします。次に、変数時間をx 軸にドラッグし、スコアをy 軸にドラッグします。
[OK]をクリックすると、次の散布図が表示されます。
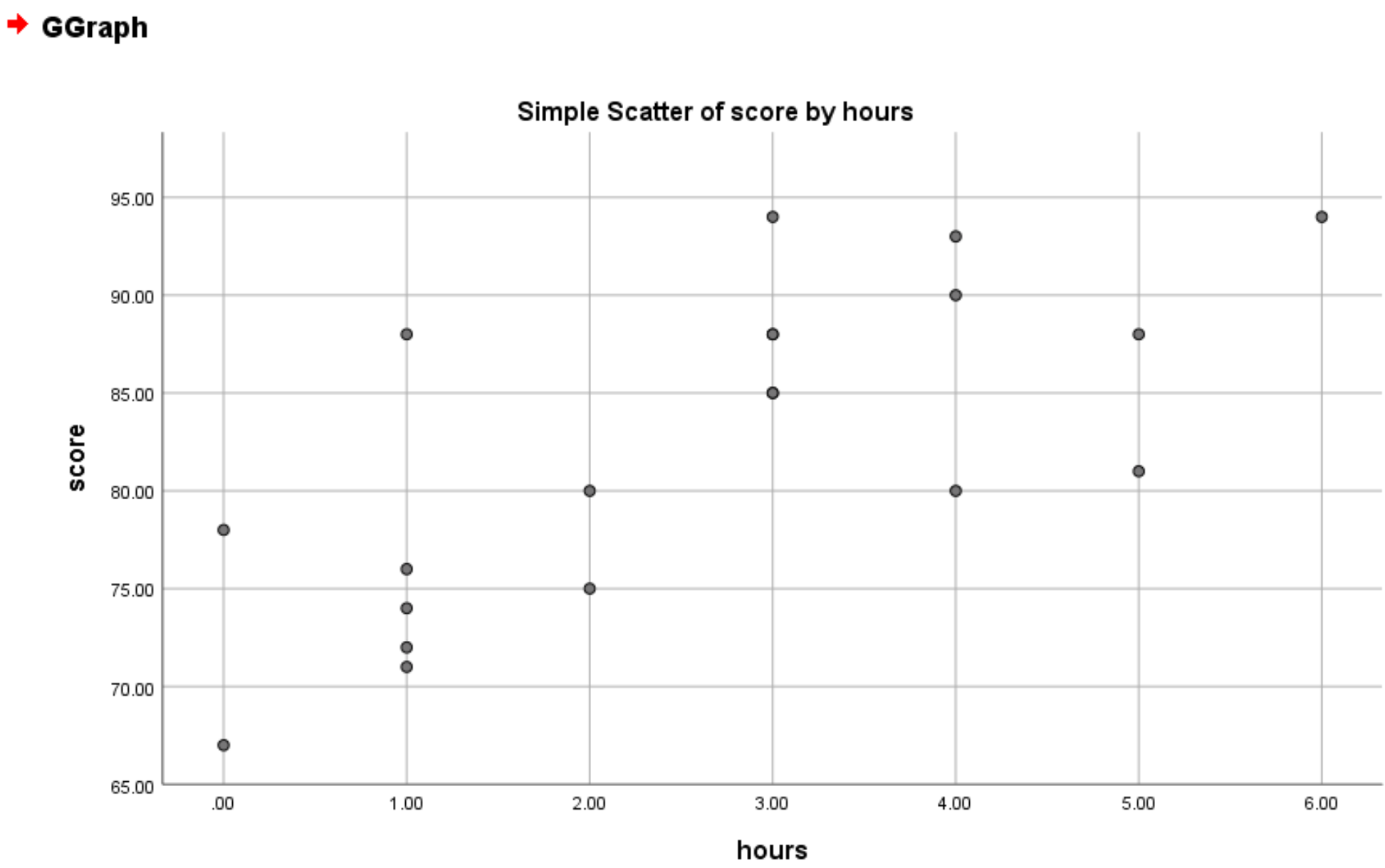
グラフから、時間とスコアの間に正の線形関係があることがわかります。一般に、より多くの時間を勉強する学生は、より高いスコアを獲得する傾向があります。
2 つの変数間には明確な線形関係があるため、単純な線形回帰モデルをデータセットに当てはめることに進みます。
ステップ 2: 単純な線形回帰モデルを当てはめます。
「分析」タブ、 「回帰」 、 「線形」の順にクリックします。
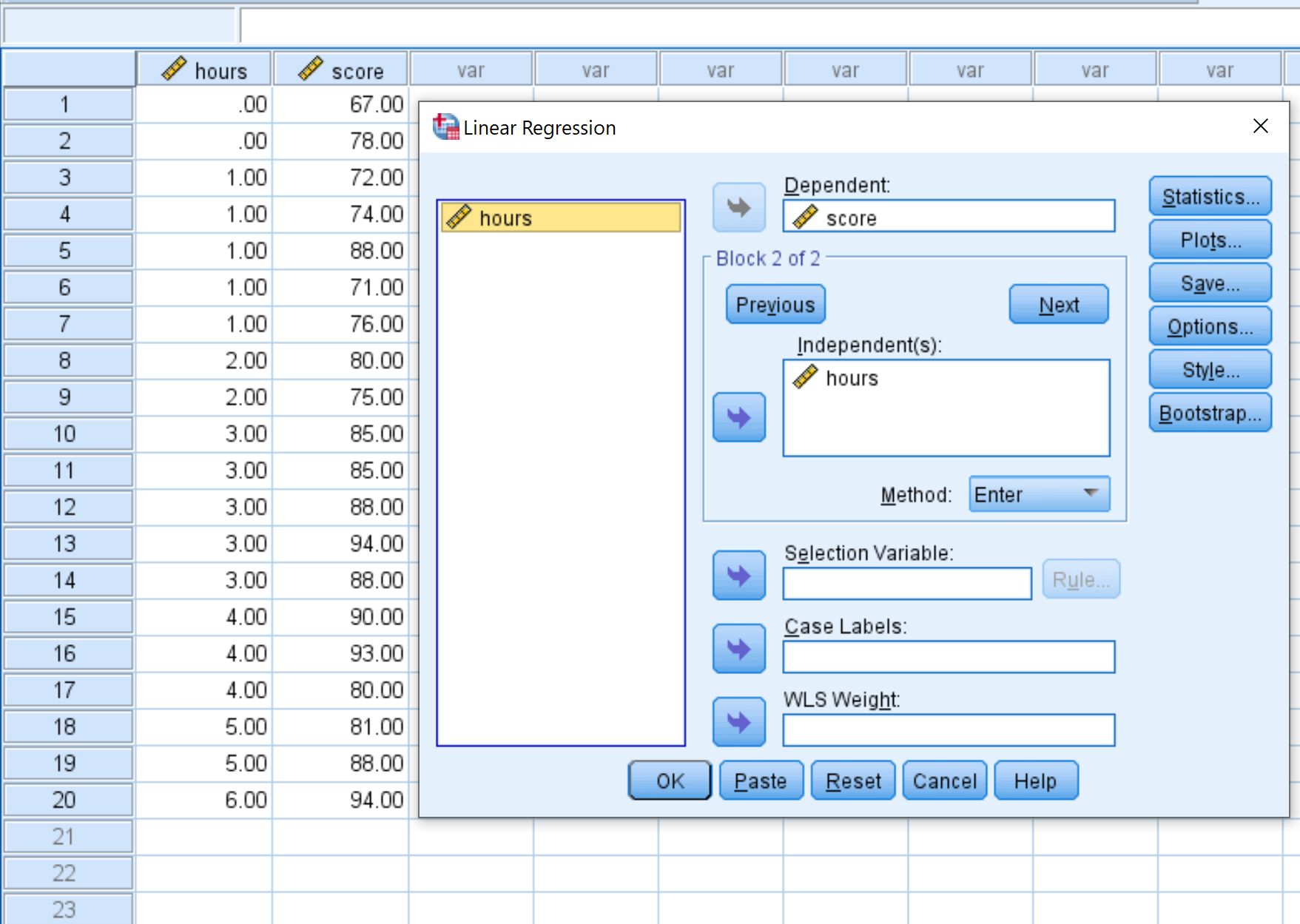
表示される新しいウィンドウで、変数スコアを「依存」というラベルのボックスにドラッグし、時間を「独立」というラベルのボックスにドラッグします。次に、 「OK」をクリックします。
ステップ 3: 結果を解釈します。
[OK]をクリックすると、単純な線形回帰の結果が表示されます。私たちにとって興味のある最初の表は、 「モデルの概要」というタイトルの表です。
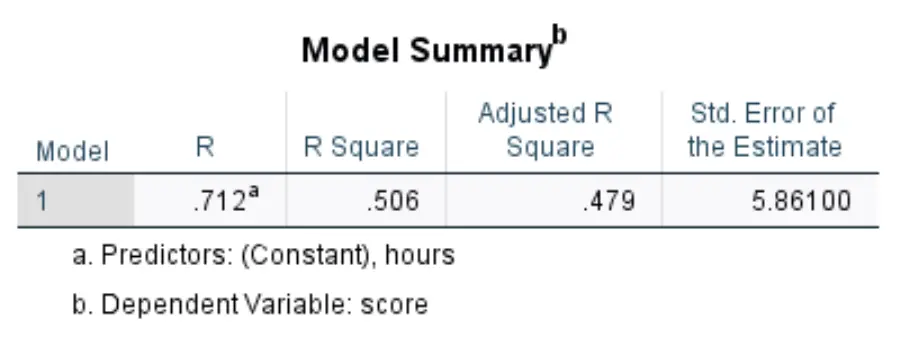
この表で最も関連性の高い数値を解釈する方法は次のとおりです。
- R 二乗:これは、説明変数によって説明できる応答変数の分散の割合です。この例では、試験得点の変動の50.6%は勉強時間によって説明できます。
- 標準。推定誤差:標準誤差は、観測値と回帰直線の間の平均距離です。この例では、観測値は回帰直線から平均5,861単位外れています。
私たちが興味を持っている次の表には、 「係数」というタイトルが付けられています。
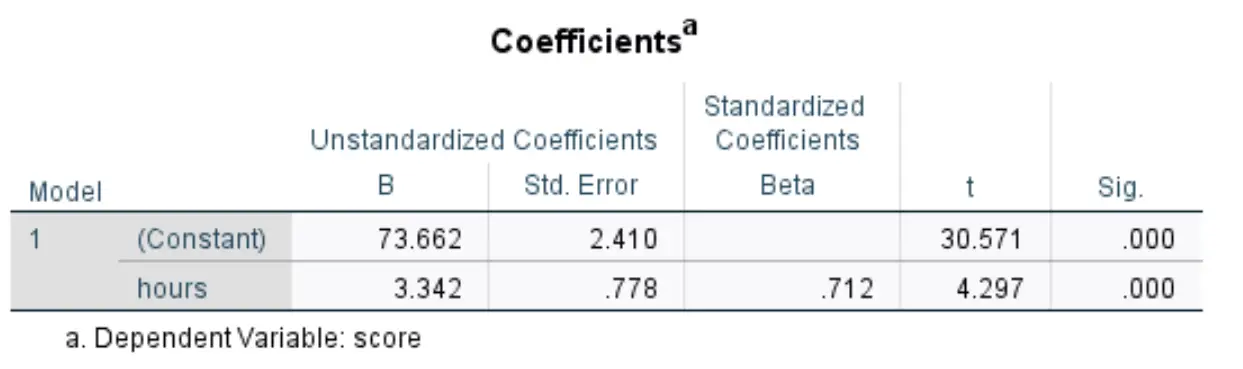
この表で最も関連性の高い数値を解釈する方法は次のとおりです。
- 非標準化 B (定数) : これは、予測変数がゼロの場合の応答変数の平均値を示します。この例では、学習時間がゼロの場合、試験の平均スコアは73.662です。
- B 非標準化 (時間):これは、予測変数の 1 単位の増加に関連する応答変数の平均変化を示します。この例では、学習時間が追加されるごとに、試験のスコアが平均3,342増加します。
- Sig (時間):これは、時間中の検定統計量に関連付けられたp 値です。この場合、この値は 0.05 未満であるため、予測変数時間は統計的に有意であると結論付けることができます。
最後に、定数と時間の値を使用して回帰式を作成できます。この場合、方程式は次のようになります。
推定試験スコア = 73.662 + 3.342*(時間)
この方程式を使用して、学習時間数に基づいて生徒の推定試験スコアを求めることができます。
たとえば、3 時間勉強した生徒は、試験スコア 83.688 を達成する必要があります。
試験の推定スコア = 73.662 + 3.342*(3) = 83.688
ステップ 4: 結果を報告します。
最後に、単純な線形回帰の結果を要約します。これを行う方法の例を次に示します。
単純な線形回帰を実行して、学習時間と試験の成績との関係を定量化しました。分析には 20 人の学生のサンプルが使用されました。
その結果、学習時間と試験の成績の間には統計的に有意な関係があり (t = 4.297、p < 0.000)、試験の成績における説明された変動の 50.6% を学習時間が占めていたことが示されました。試験。
回帰式は次のようになりました。
推定試験スコア = 73.662 + 3.342*(時間)
学習時間が追加されるごとに、試験のスコアは平均3,342増加します。
追加リソース
次のチュートリアルでは、SPSS で他の一般的なタスクを実行する方法について説明します。