Spss で重回帰を実行する方法
重線形回帰は、 2 つ以上の説明変数と応答変数の間の関係を理解するために使用できる方法です。
このチュートリアルでは、SPSS で重線形回帰を実行する方法について説明します。
例: SPSS での重線形回帰
勉強に費やした時間数と受けた模擬試験の数が、学生が特定の試験で受け取る成績に影響するかどうかを知りたいとします。これを調べるために、次の変数を使用して重回帰を実行できます。
説明変数:
- 勉強時間
- 予備試験に合格しました
応答変数:
- 試験の結果
SPSS でこの重線形回帰を実行するには、次の手順を使用します。
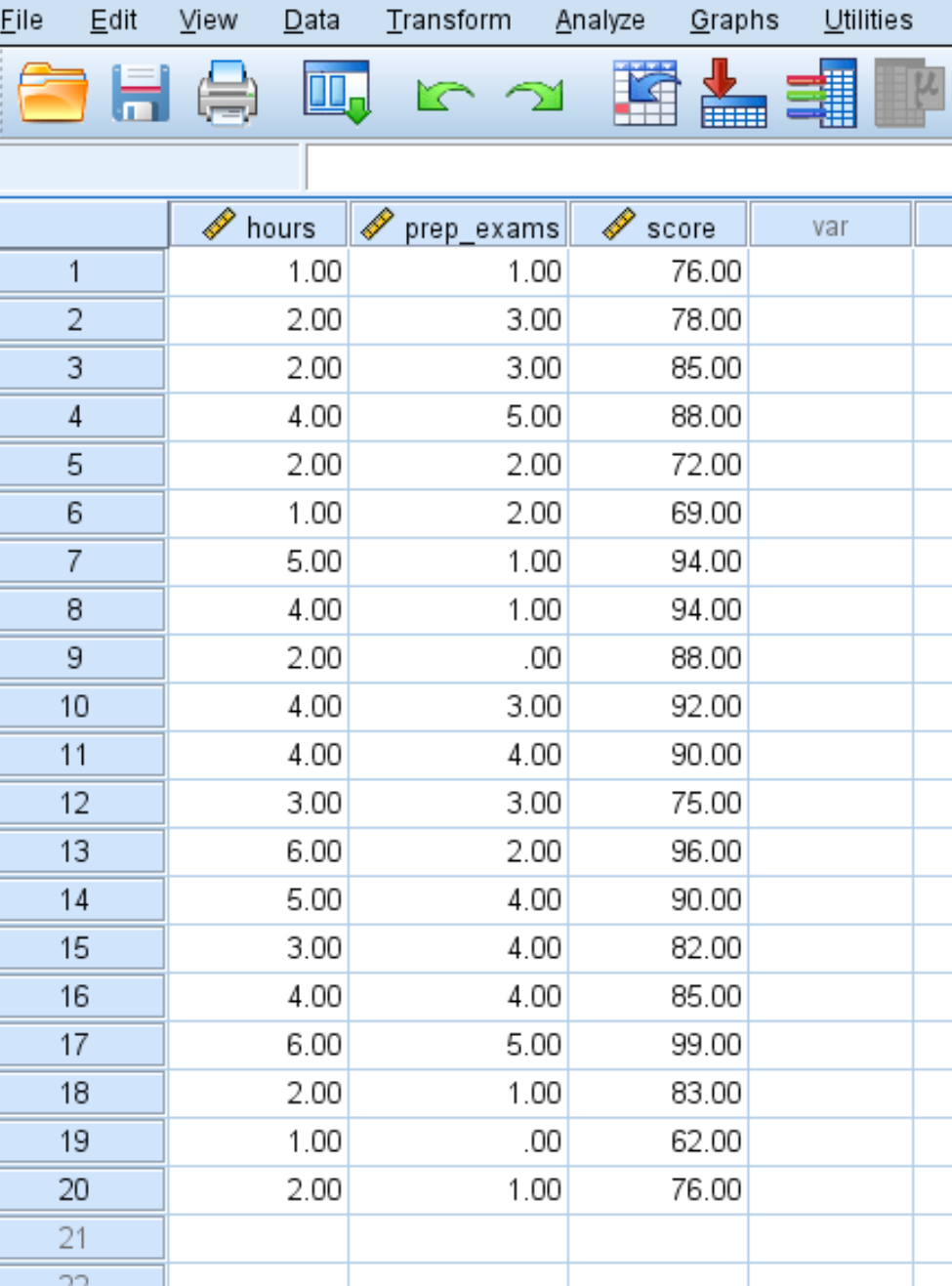
ステップ 1: データを入力します。
20 人の学生の学習時間数、受験した予備試験、および受け取った試験結果に関する次のデータを入力します。
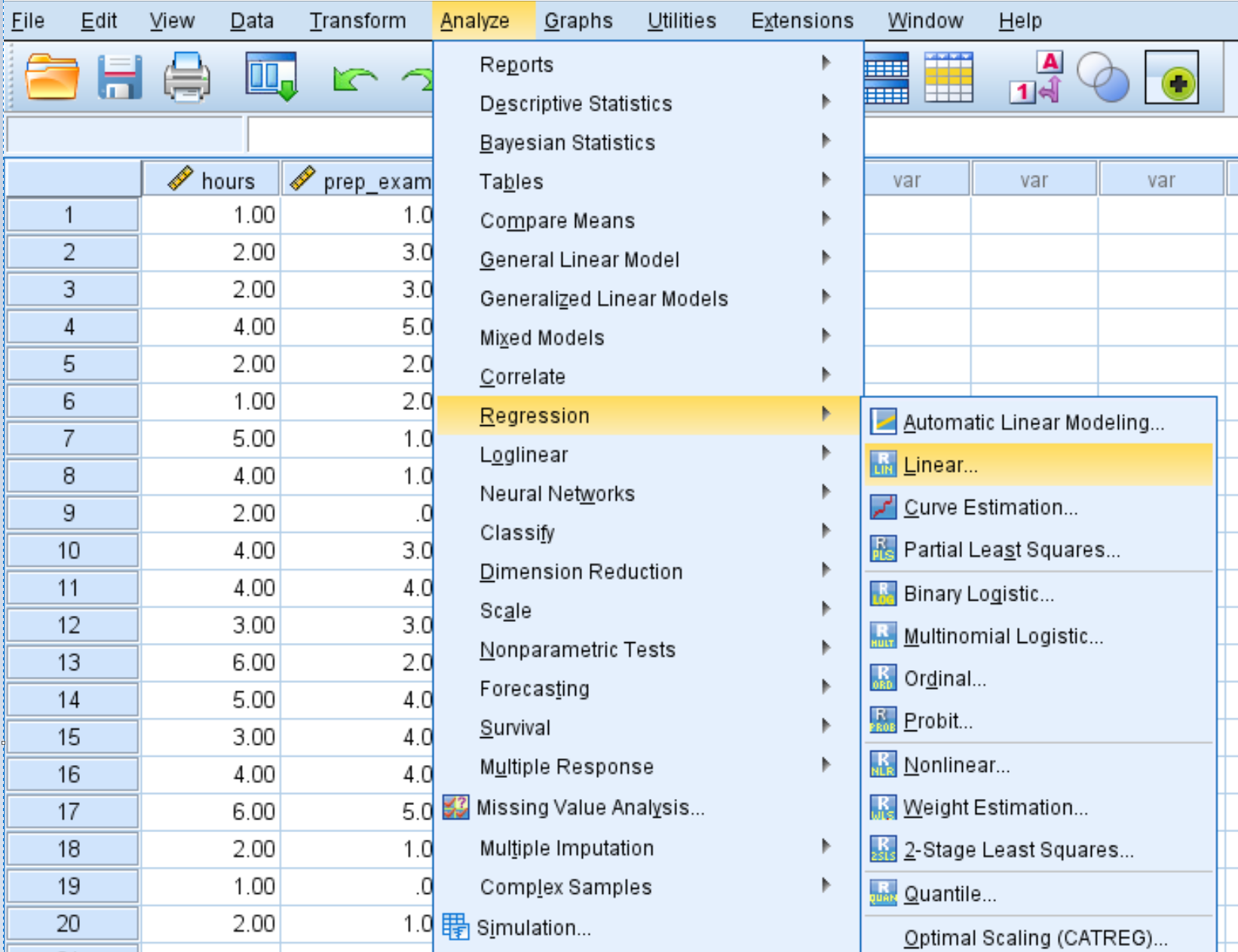
ステップ 2: 重回帰を実行します。
「分析」タブ、 「回帰」 、 「線形」の順にクリックします。
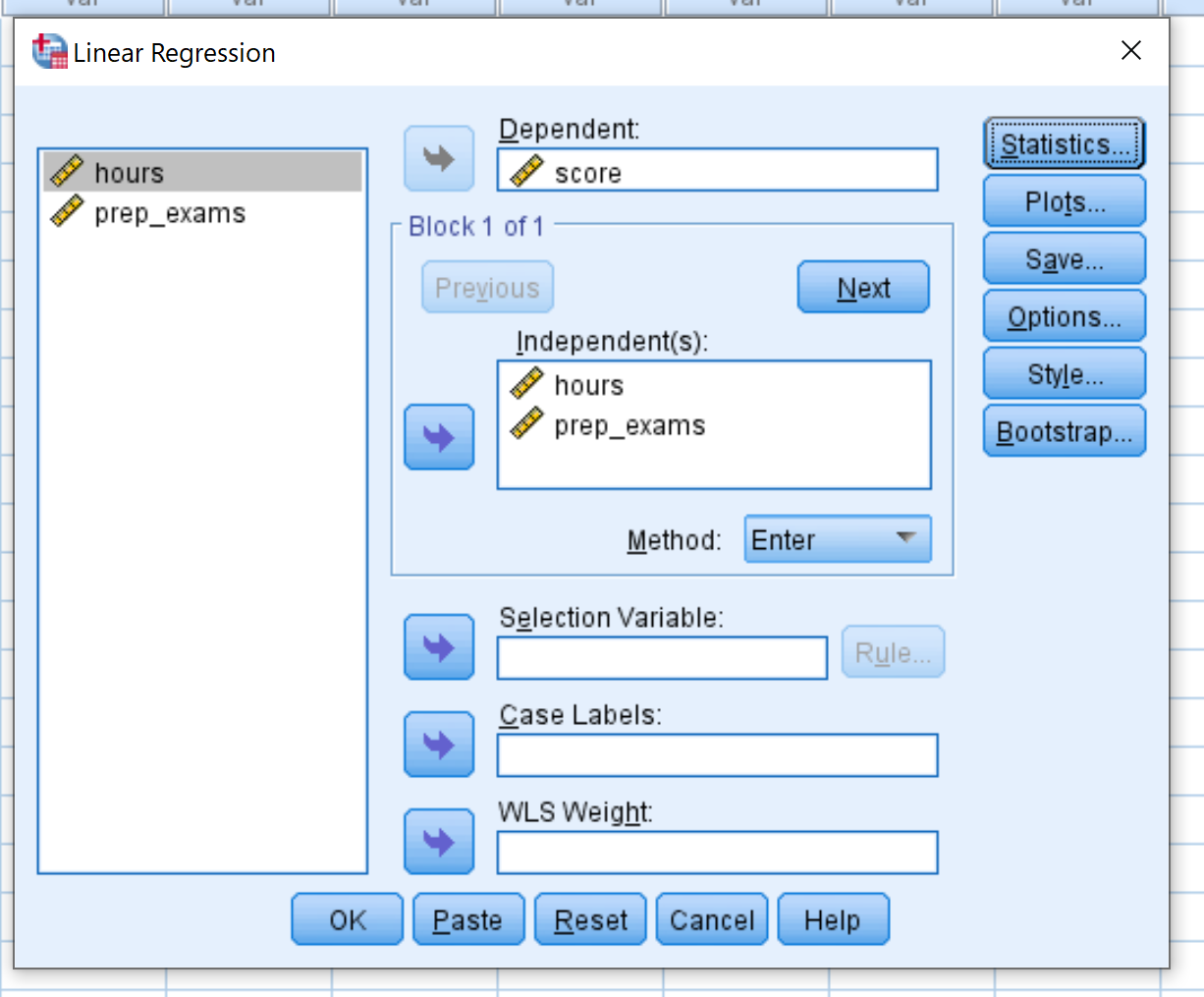
変数スコアを「依存」というラベルのボックスにドラッグします。時間変数とprep_exams変数を「Independent(s)」というラベルのボックスにドラッグします。次に、 「OK」をクリックします。
ステップ 3: 結果を解釈します。
[OK]をクリックすると、多重線形回帰の結果が新しいウィンドウに表示されます。
興味のある最初のテーブルは、 「モデルの概要」と呼ばれます。
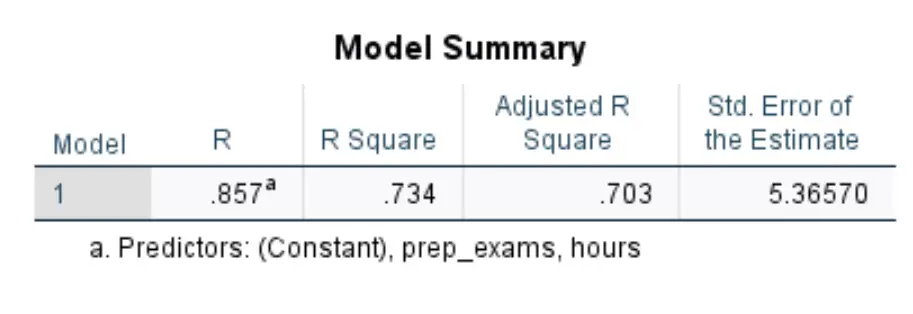
この表で最も関連性の高い数値を解釈する方法は次のとおりです。
- R 二乗:これは、説明変数によって説明できる応答変数の分散の割合です。この例では、試験スコアの変動の73.4%は、勉強時間と受験した予備試験の数によって説明できます。
- 標準。推定誤差:標準誤差は、観測値と回帰直線の間の平均距離です。この例では、観測値は回帰直線から平均して5.3657単位外れています。
私たちが興味を持っている次のテーブルはANOVAと呼ばれます。
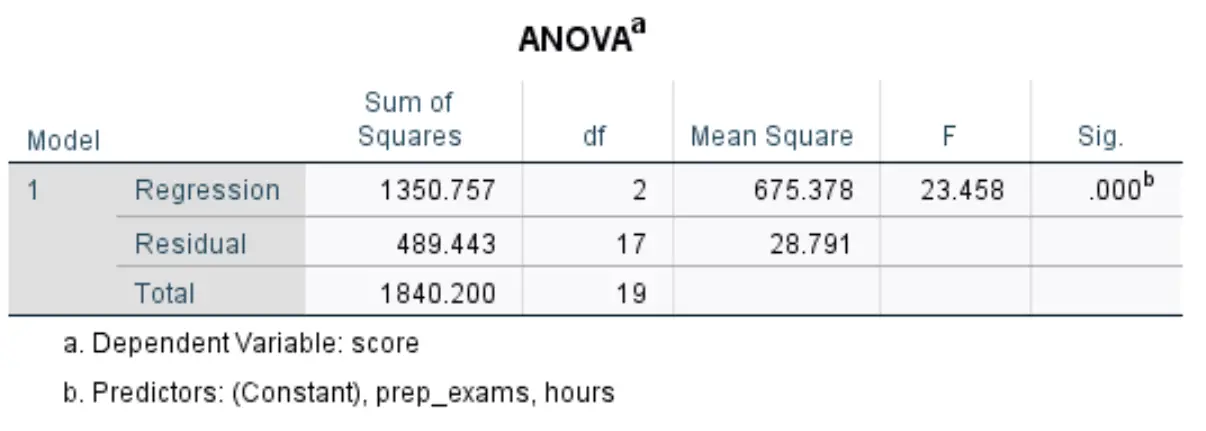
この表で最も関連性の高い数値を解釈する方法は次のとおりです。
- F:これは回帰モデルの全体的な F 統計量であり、平均二乗回帰 / 平均二乗残差として計算されます。
- Sig:これは、全体的な F 統計量に関連付けられた p 値です。これにより、回帰モデル全体が統計的に有意であるかどうかがわかります。言い換えれば、組み合わせた 2 つの説明変数が応答変数と統計的に有意な関連性を持っているかどうかがわかります。この場合、p 値は 0.000 に等しく、これは説明変数、学習時間、および受験した予備試験が試験結果と統計的に有意な関連性があることを示します。
私たちが興味を持っている次の表には、 「係数」というタイトルが付けられています。
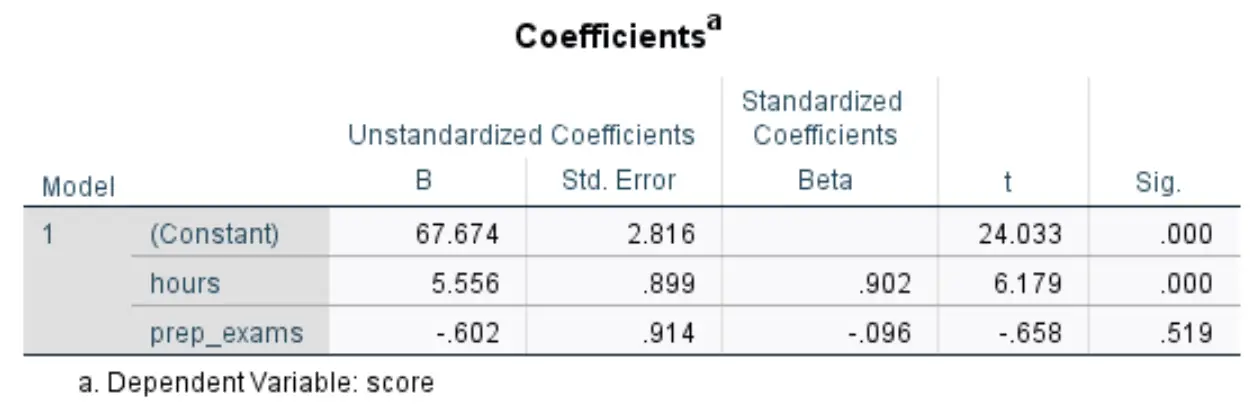
この表で最も関連性の高い数値を解釈する方法は次のとおりです。
- B 非標準化 (定数):これは、両方の予測子変数がゼロである場合の応答変数の平均値を示します。この例では、学習時間と受験した予備試験の時間が両方とも 0 の場合、試験の平均スコアは67,674です。
- 非標準化 B (時間):これは、受験した予備試験の数が一定であると仮定した場合、学習時間の 1 単位の増加に伴う試験スコアの平均変化を示します。この場合、受験した模擬試験の数が一定であると仮定すると、勉強に費やす時間が 1 時間増えるごとに、試験のスコアは5,556ポイント増加します。
- 非標準化 B (prep_exams):これは、学習時間数が一定であると仮定した場合、受験する予備試験の 1 単位増加に伴う試験スコアの平均変化を示します。この場合、学習時間数が一定であると仮定すると、追加の予備試験を受けるたびに試験スコアが0.602ポイント減少します。
- シグ。 (時間):これは、説明変数hoursの p 値です。この値 (0.000) は 0.05 未満であるため、学習時間は試験のスコアと統計的に有意な関連があると結論付けることができます。
- シグ。 (prep_exams):これは、 prep_exams説明変数の p 値です。この値 (0.519) は 0.05 未満ではないため、予備試験の受験数が試験の結果と統計的に有意な関連があると結論付けることはできません。
最後に、表に示されているconstant 、 hours 、およびprep_examsの値を使用して回帰式を作成できます。この場合、方程式は次のようになります。
推定試験スコア = 67.674 + 5.556*(時間) – 0.602*(prep_exams)
この式を使用して、学習時間数と受験した模擬試験の数に基づいて、生徒の推定試験スコアを求めることができます。たとえば、3 時間勉強して 2 つの予備試験を受けた学生は、試験スコア 83.1 を取得する必要があります。
試験の推定スコア = 67.674 + 5.556*(3) – 0.602*(2) = 83.1
注:予備試験の説明変数は統計的に有意であることが判明しなかったため、モデルからそれを削除し、代わりに唯一の説明変数として学習時間を使用して単純な線形回帰を実行することを決定できます。