Spss でロジスティック回帰を実行する方法

ロジスティック回帰は、応答変数がバイナリの場合に回帰モデルを近似するために使用する方法です。

このチュートリアルでは、SPSS でロジスティック回帰を実行する方法を説明します。

例: SPSS でのロジスティック回帰

次の手順を使用して、GPA に基づいて大学バスケットボール選手が NBA にドラフトされたかどうか (ドラフト: 0 = いいえ、1 = はい) を示すデータ セットに対して SPSS でロジスティック回帰を実行します。試合ごとのポイントとその部門レベル。

ステップ 1: データを入力します。

まず、次のデータを入力します。

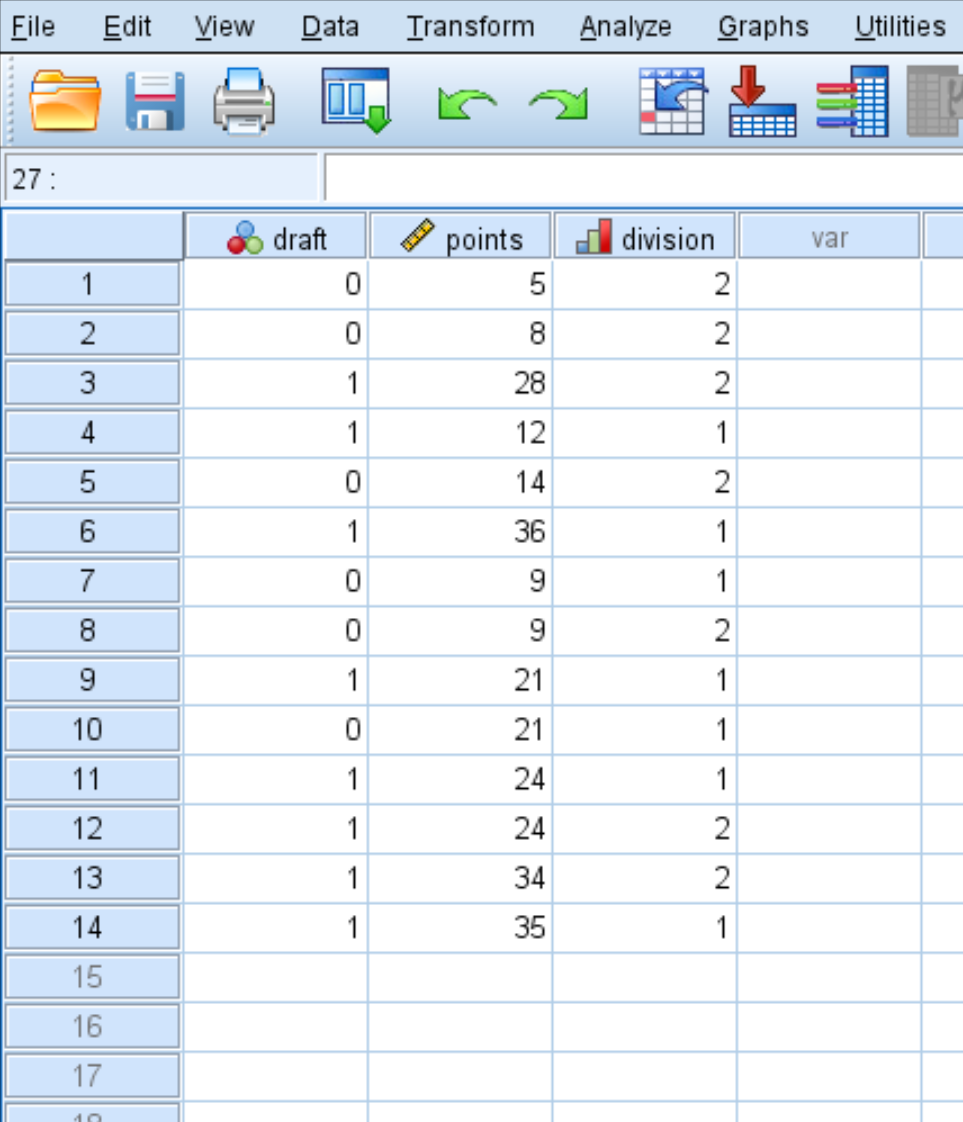
ステップ 2: ロジスティック回帰を実行します。

[分析]タブ、 [回帰] 、 [バイナリ ロジスティック回帰]の順にクリックします。

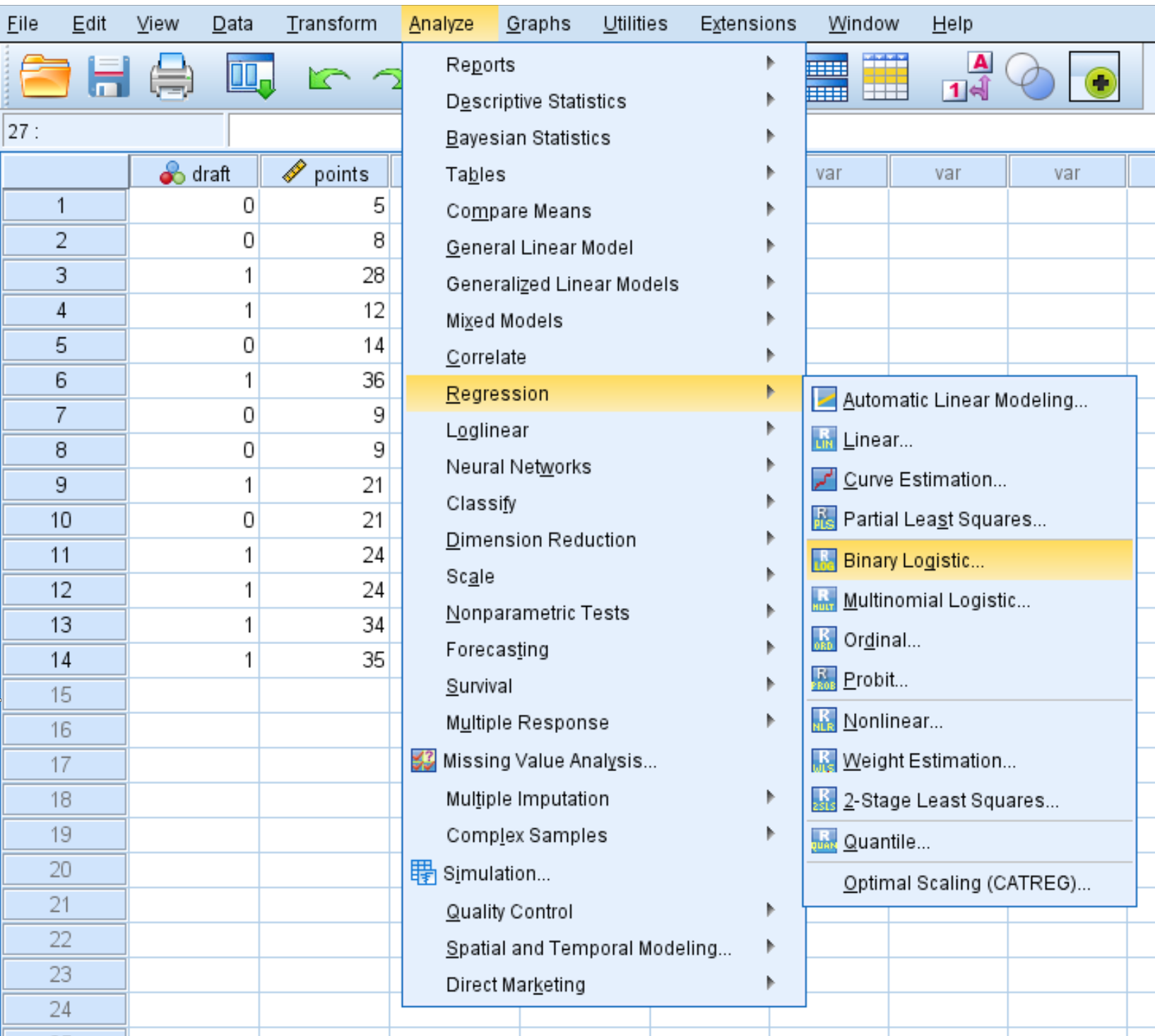
表示される新しいウィンドウで、バイナリ応答変数プロジェクトを「Dependent」というラベルの付いた領域にドラッグします。次に、予測子変数のコロンと除算を「Block 1 of 1」というラベルの付いたボックスにドラッグします。メソッドは Enter に設定したままにしておきます。次に、 「OK」をクリックします。

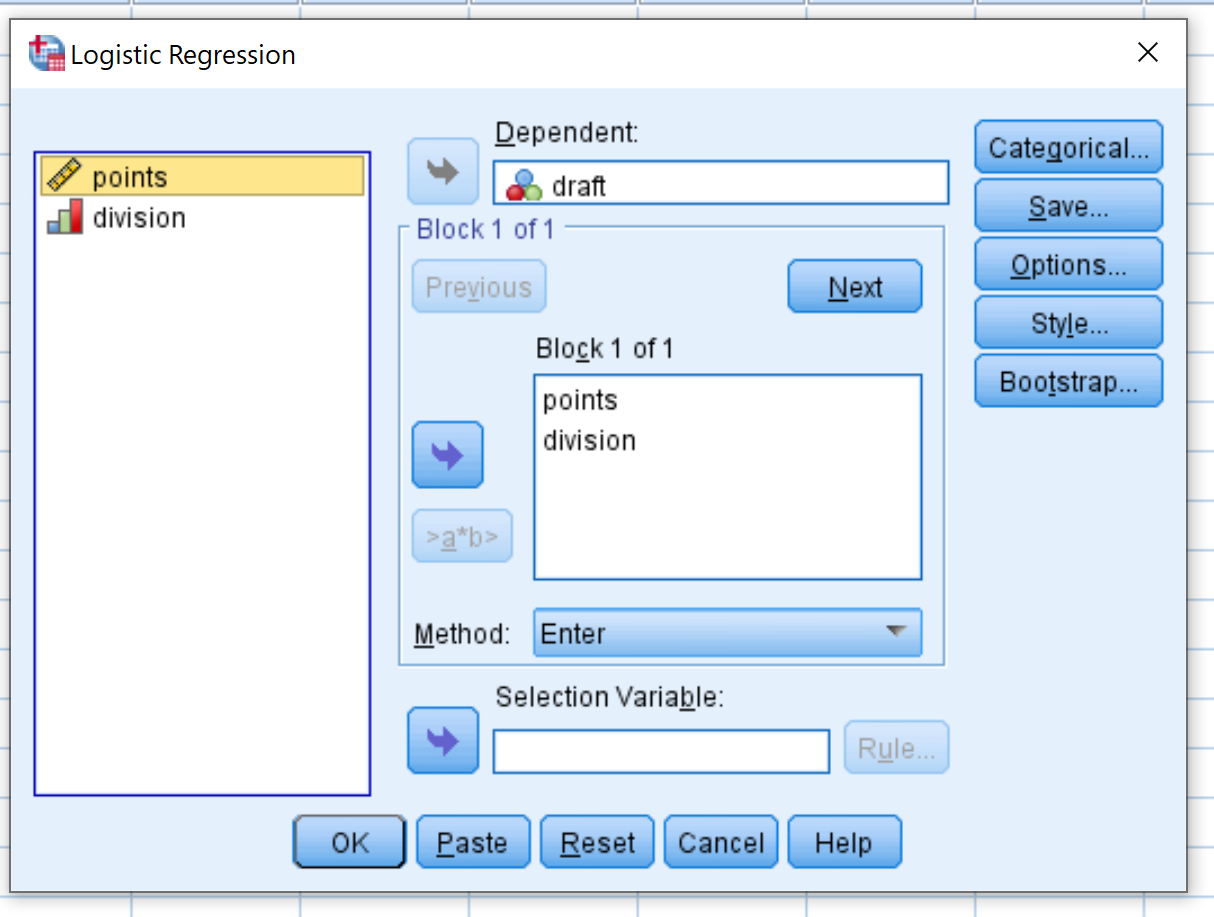
ステップ 3. 結果を解釈します。

[OK]をクリックすると、ロジスティック回帰の結果が表示されます。

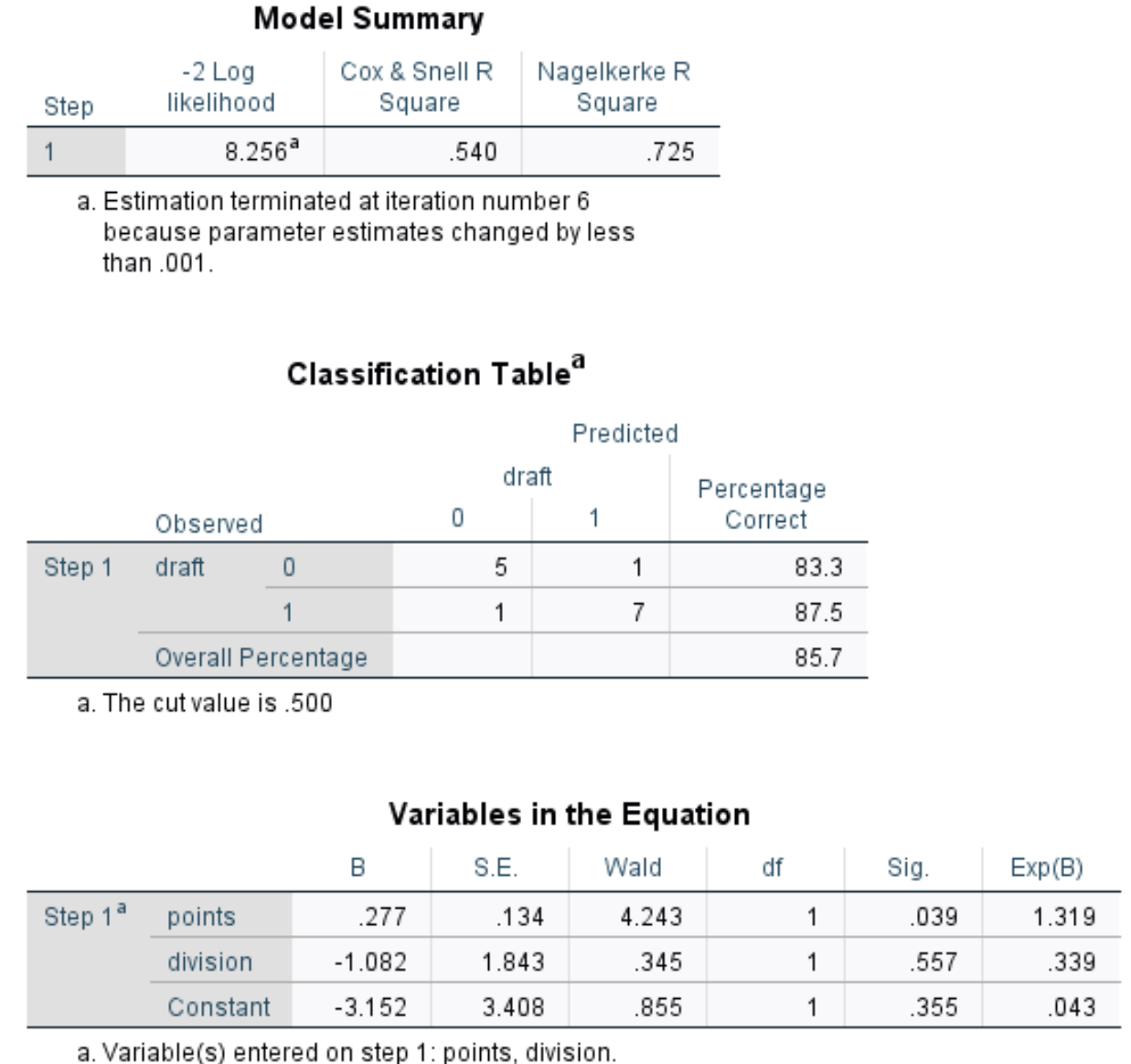
結果を解釈する方法は次のとおりです。

モデルの概要:この表で最も有用なメトリクスは、予測変数によって説明できる応答変数の変動のパーセンテージを示すナーゲルケルケ R 二乗です。この場合、ポイントと分割によってドラフト変動の72.5%を説明できます。

分類テーブル:このテーブルで最も役立つ指標は全体のパーセンテージであり、モデルが正しく分類できた観測値のパーセンテージを示します。この場合、ロジスティック回帰モデルは85.7%の選手のドラフト結果を正確に予測できました。

方程式内の変数:この最後の表は、次のようないくつかの有用な測定値を提供します。

• Wald:各予測子変数の Wald 検定統計量。各予測子変数が統計的に有意かどうかを判断するために使用されます。
• Sig:各予測子変数の Wald 検定統計量に対応する p 値。点の p 値は 0.039、除算の p 値は 0.557 であることがわかります。
• Exp(B):各予測子変数のオッズ比。これは、特定の予測変数の 1 単位の増加に関連して、プレーヤーがドラフトされるオッズの変化を示します。たとえば、ディビジョン 2 のプレーヤーがドラフトされるオッズは、ディビジョン 1 のプレーヤーがドラフトされるオッズのわずか 0.339 です。同様に、ゲームごとのポイントの追加ユニットごとの増加は、プレーヤーがドラフトされるオッズの 1,319 増加に関連付けられます。

次に、次の式を使用して、係数 (B というラベルが付いた列の値) を使用して、特定のプレーヤーがドラフトされる確率を予測できます。

確率 = e ^{-3.152 + 0.277 (ポイント) – 1.082 (除算)} / (1+e ^{-3.152 + 0.277 (ポイント) – 1.082 (除算)} )

たとえば、1 試合あたり平均 20 得点を獲得し、ディビジョン 1 でプレーするプレーヤーがドラフトされる確率は、次のように計算できます。

確率 = e ^{-3.152 + 0.277(20) – 1.082(1)} / (1+e ^{-3.152 + 0.277(20) – 1.082(1)} ) = 0.787 。

この確率は 0.5 より大きいため、このプレーヤーがドラフトされると予測します。

ステップ 4. 結果を報告します。

最後に、ロジスティック回帰の結果を報告したいと思います。これを行う方法の例を次に示します。

ロジスティック回帰を実行して、ゲームごとのポイントと部門レベルがバスケットボール選手のドラフトされる確率にどのような影響を与えるかを判断しました。分析には合計 14 人のプレーヤーが使用されました。

このモデルはプロジェクト結果の変動の 72.5% を説明し、ケースの 85.7% を正しく分類しました。

ディビジョン 2 の選手がドラフトされるオッズは、ディビジョン 1 の選手がドラフトされるオッズのわずか 0.339 でした。

1試合あたりのポイントが追加で増加するごとに、プレイヤーがドラフトされる確率が1,319増加しました。