T スコアと z スコア: いつ使用するか?
統計コースで学生がよく混乱する 2 つの用語は、 t スコアとZ スコアです。
どちらも仮説検定の実行時や信頼区間の構築時に広く使用されていますが、若干異なります。
それぞれの式は次のとおりです。
スコア t = ( x – μ) / (s/√ n )
金:
- x : サンプル平均
- μ : 母集団平均
- s : サンプルの標準偏差
- n : サンプルサイズ
z スコア = ( x – μ) / σ
金:
- x : 生データの値
- μ : 母集団平均
- σ : 母集団標準偏差
このフローチャートは、データに基づいて、それぞれをいつ使用する必要があるかを示しています。
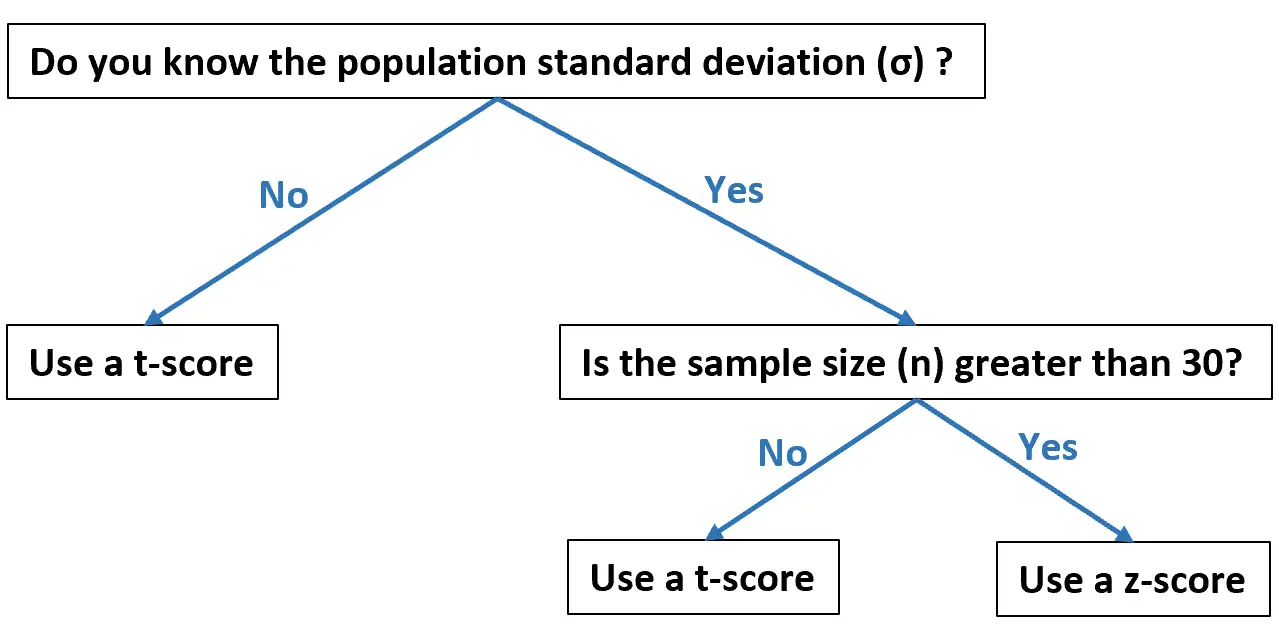
次の例は、実際に T スコアと Z スコアを計算する方法を示しています。
例 1: T スコアの計算
レストランが平均重量 μ = 0.25 ポンドであると主張するハンバーガーを調理するとします。
n = 20 個のハンバーガーのランダムなサンプルを取得し、サンプルの平均重量がx = 0.22 ポンド、標準偏差 s = 0.05 ポンドであることが判明したとします。仮説検定を実行して、このレストランで製造されているすべてのハンバーガーの実際の平均重量が 0.25 ポンドに等しいかどうかを判断します。
この例では、次の 2 つの条件がどちらも満たされないため、 T スコアを使用して仮説検定を実行します。
- 母集団の標準偏差 (σ) は既知です。 (この例ではσは与えられていません)
- サンプル サイズが 30 を超えています。(この例では n=20)
したがって、t スコアは次のように計算されます。
- スコア t = ( x – μ) / (s/√ n )
- t スコア = (0.22 – 0.25) / (0.05 / √ 20 )
- t スコア = -2.68
P 値 T スコア計算機によると、この t スコアに対応する p 値は0.01481です。
この p 値は 0.05 未満であるため、このレストランで製造されるハンバーガーの平均重量は 0.25 ポンドに等しくないという十分な証拠があります。
例 2: Z スコアの計算
ある企業が製造しているバッテリーの寿命が、平均 μ = 20 時間、標準偏差 σ = 5 時間の正規分布に従うことがわかっていると仮定します。
n = 50 個のバッテリーのランダムなサンプルを取得し、サンプルの平均がx = 21 時間であることが判明したとします。仮説テストを実行して、この会社が製造するすべてのバッテリーの真の平均寿命が 20 時間に等しいかどうかを判断します。
この例では、次の条件が両方とも満たされるため、 Z スコアを使用して仮説検定を実行します。
- 母集団の標準偏差 (σ) は既知です。 (この例では σ は 5 に等しい)
- サンプル サイズが 30 を超えています。(この例では n=50)
したがって、Z スコアは次のように計算されます。
- z スコア = ( x – μ) / σ
- Z スコア = (21 – 20) / 5
- Z スコア = 0.2
P 値 Z スコア計算ツールによると、この Z スコアに対応する p 値は0.84184です。
この p 値は 0.05 未満ではないため、この会社が製造するすべてのバッテリーの平均寿命が 20 時間とは異なると言える十分な証拠はありません。
追加リソース
次のチュートリアルでは、T スコアと Z スコアについて詳しく説明します。