Python で t 分布を使用する方法
t 分布は、正規分布よりも重い「裾」があることを除いて、正規分布に似た確率分布です。
言い換えると、正規分布と比較すると、分布内の値が中心よりも端に多く配置されます。
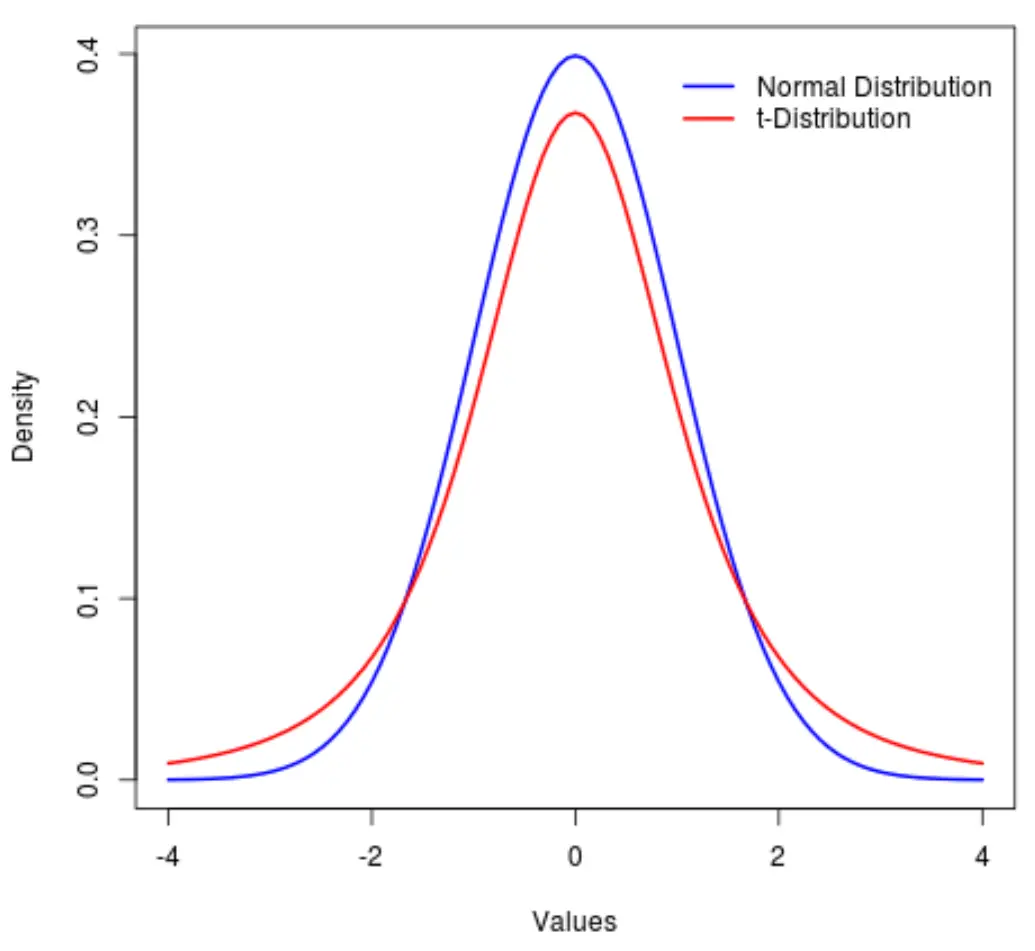
このチュートリアルでは、Python で t 分布を使用する方法を説明します。
生成から配布までの方法
t.rvs(df, size)関数を使用すると、特定の自由度とサンプル サイズの分布からランダムな値を生成できます。
from scipy. stats import t #generate random values from t distribution with df=6 and sample size=10 t. rvs (df= 6 , size= 10 ) array([-3.95799716, -0.01099963, -0.55953846, -1.53420055, -1.41775611, -0.45384974, -0.2767931, -0.40177789, -0.3602592, 0.38262431])
結果は、6 自由度の分布に従って互いに続く 10 個の値のテーブルになります。
t分布を使用したP値の計算方法
関数t.cdf(x, df, loc=0,scale=1) を使用して、t 検定統計量に関連付けられた p 値を見つけることができます。
例 1: 片側 P 値を求める
片側仮説検定を実行し、検定統計量-1.5および自由度 = 10が得られたとします。
次の構文を使用して、この検定統計量に対応する p 値を計算できます。
from scipy. stats import t #calculate p-value t. cdf (x=-1.5, df=10) 0.08225366322272008
10 自由度での検定統計量 -1.5 に対応する片側 p 値は0.0822です。
例 2: 二元配置 P 値を求める
両側仮説検定を実行し、検定統計量2.14および自由度 = 20が得られたとします。
次の構文を使用して、この検定統計量に対応する p 値を計算できます。
from scipy. stats import t #calculate p-value (1 - t. cdf (x=2.14, df=20)) * 2 0.04486555082549959
20 自由度の検定統計量 2.14 に対応する両側 p 値は0.0448です。
注: これらの答えは、逆 t 分布計算ツールを使用して確認できます。
配布まで追跡する方法
次の構文を使用して、特定の自由度で分布をプロットできます。
from scipy. stats import t import matplotlib. pyplot as plt #generate t distribution with sample size 10000 x = t. rvs (df= 12 , size= 10000 ) #create plot of t distribution plt. hist (x, density= True , edgecolor=' black ', bins= 20 )
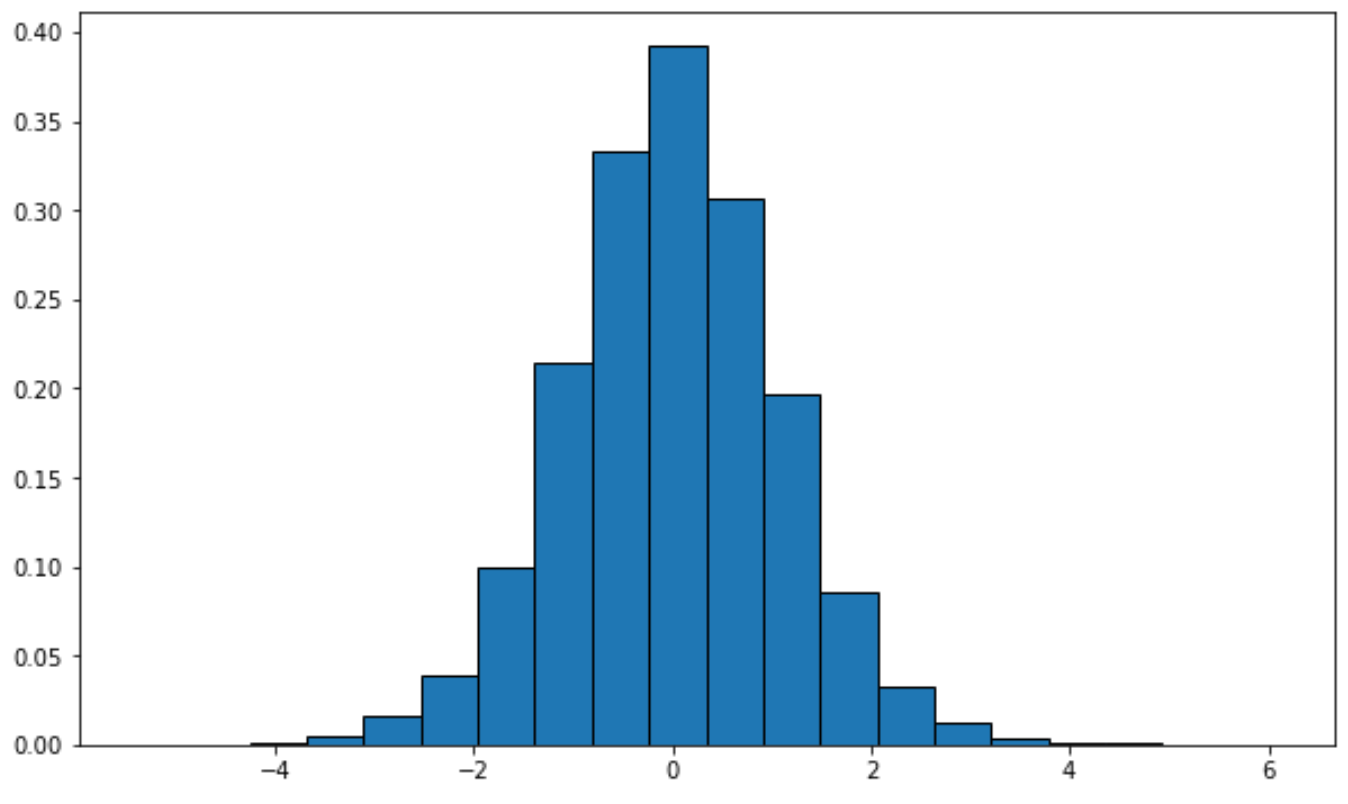
あるいは、 seaborn視覚化パッケージを使用して密度曲線を作成することもできます。
import seaborn as sns #create density curve sns. kdeplot (x)
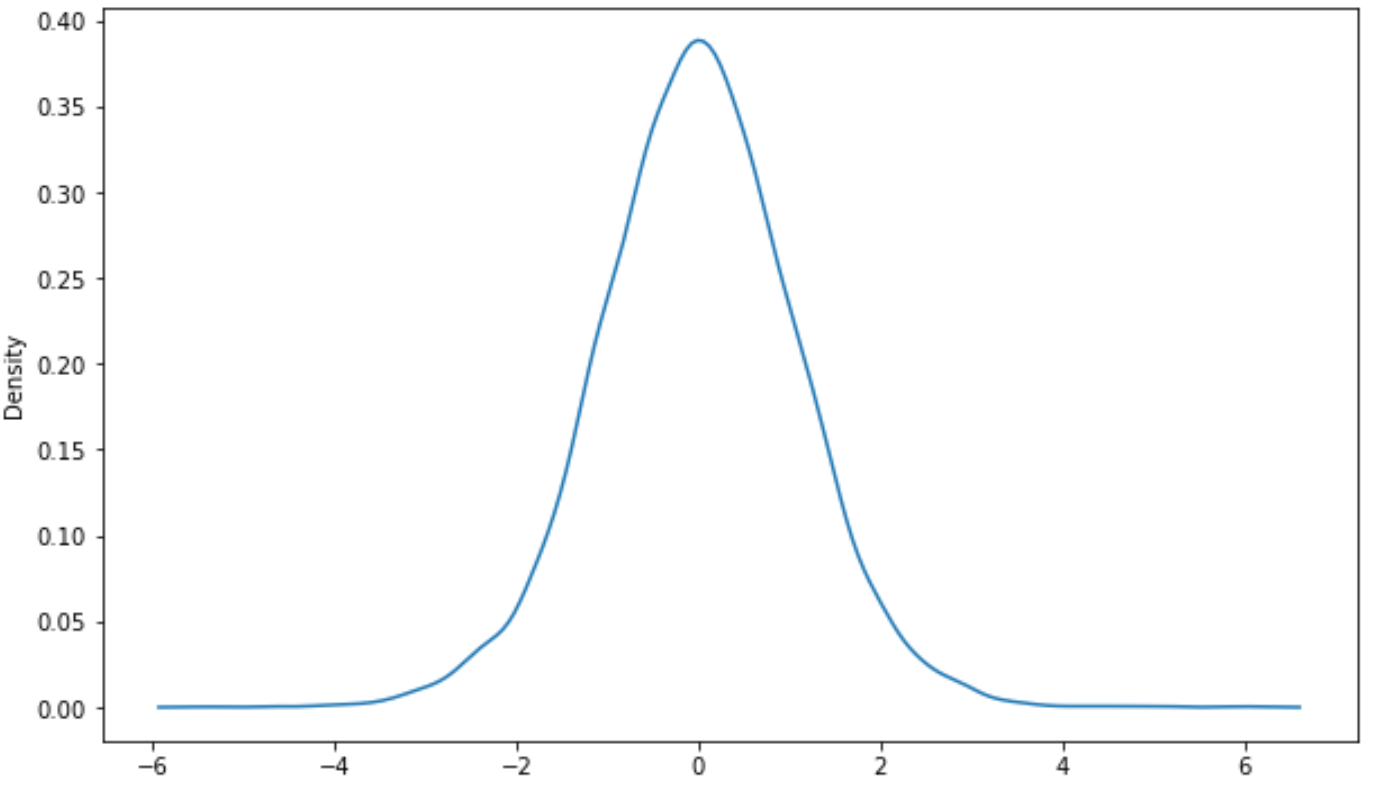
追加リソース
次のチュートリアルでは、ディストリビューションに関する追加情報を提供します。
正規分布と t 分布: 違いは何ですか?
逆t分布計算機