Excel で t スコアから p 値を見つける方法
統計では、仮説検定の結果として T スコア検定統計が得られることがよくあります。 t スコアが見つかったら、通常はそれに関連する p 値が見つかります。この p 値が特定のアルファ レベル (0.10、0.05、0.01 など) を下回る場合、検定の帰無仮説は棄却され、結果は有意であると結論付けられます。
このチュートリアルでは、次の引数を受け取るT.DIST関数を使用して Excel で t スコアから p 値を見つける方法について説明します。
T.DIST (x, 自由度)
金:
- x:関心のある T スコア。
- deg_freedom:自由度。
いくつかの例を見てみましょう。
例 1: t スコアからの P 値 (両側)
植物学者は、特定の植物種の平均高さが 15 インチに等しいかどうかを知りたいと考えています。 12 本の植物からなる ランダム サンプルで、彼女はサンプルの平均高さが 14.33 インチ、サンプルの標準偏差が 1.37 インチであることを発見しました。
アルファ レベル 0.05 を使用して両側仮説検定を実行し、平均身長が 15 インチに等しいかどうかを判断します。
ステップ 1:仮説を述べます。
帰無仮説 (H 0 ): μ = 15
対立仮説: (Ha): μ ≠ 15
ステップ 2: T スコアと自由度を求めます。
スコア t = ( x -μ) / (s/√n) = (14.33-15) / (1.37/√12) = -1.694 。
自由度 = n-1 = 12-1 = 11 。
ステップ 3: Excel を使用して t スコアの p 値を見つけます。
t スコアの p 値を見つけるには、Excel で次の式を使用します。
=T.DIST.2T(ABS(-1.694), 11)
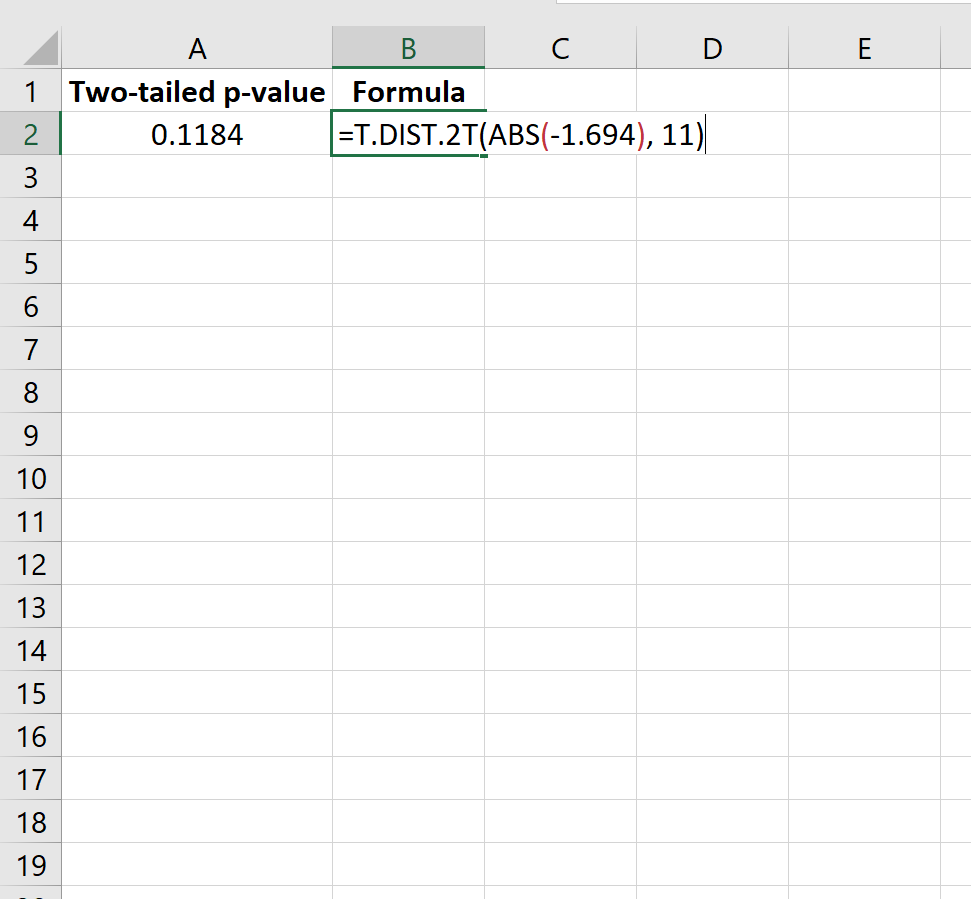
これは、両側 p 値が0.1184であることを示します。
ステップ 4: 帰無仮説を拒否するか、拒否しません。
p 値0.1184は選択されたアルファ レベル0.05より小さくないため、帰無仮説を棄却できません。平均的な植物の高さが15インチよりも異なると言える十分な証拠はありません。
例 2: T スコアからの P 値 (片側)
ある企業は、新しいタイプのバッテリーの平均寿命が、平均寿命が 18 時間である現在の標準バッテリーよりも長いかどうかを知りたいと考えています。 25 個の新しいバッテリーの 無作為サンプルでは、平均寿命が 19 時間、標準偏差が 4 時間であることがわかりました。
アルファ レベル 0.05 を使用して片側仮説検定を実行し、新しいバッテリの平均寿命が現在の標準バッテリの平均寿命より長いかどうかを判断します。
ステップ 1:仮説を述べます。
帰無仮説 (H 0 ): μ ≤ 18
対立仮説: (Ha): μ > 18
ステップ 2: T スコアと自由度を求めます。
スコア t = ( x -μ) / (s/√n) = (19-18) / (4/√25) = 1.25 。
自由度 = n-1 = 25-1 = 24 。
ステップ 3: Excel を使用して t スコアの p 値を見つけます。
t スコアの p 値を見つけるには、Excel で次の式を使用します。
=T.DIST.RT(1.25, 24)
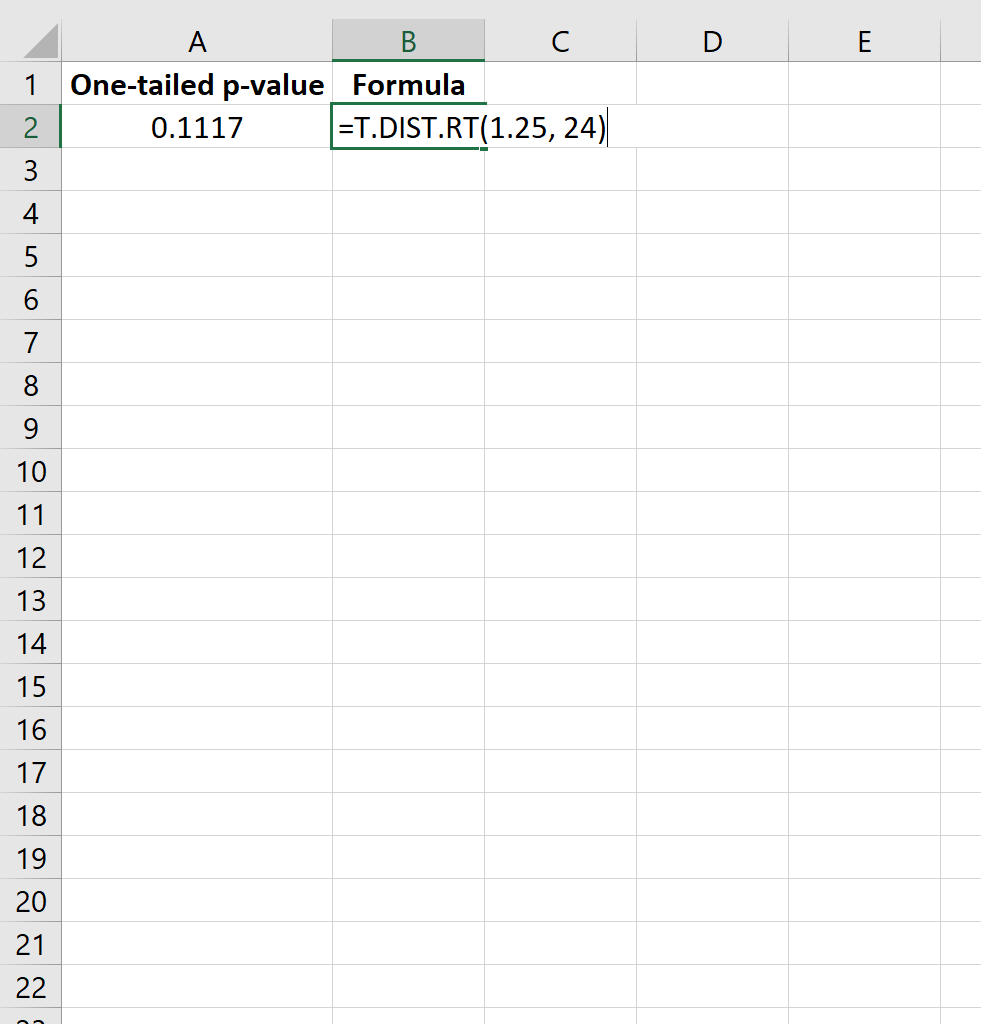
これは、片側 p 値が0.1117であることを示しています。
ステップ 4: 帰無仮説を拒否するか、拒否しません。
p 値0.1117は選択されたアルファ レベル0.05より大きいため、帰無仮説を棄却できません。新しいバッテリーの平均寿命が現在の標準バッテリーの平均寿命よりも長いと言える十分な証拠はありません。
Excel の統計に関するその他のチュートリアルについては、 Excel ガイドの完全なリストを必ずご確認ください。