線形回帰における t 検定を理解する
線形回帰は、予測変数と応答変数の間の関係を定量化するために使用されます。
線形回帰を実行するときは常に、予測変数と応答変数の間に統計的に有意な関係があるかどうかを知りたいと考えます。
回帰勾配の t 検定を実行することで有意性を検定します。この t 検定には次の帰無仮説と対立仮説を使用します。
- H 0 : β 1 = 0 (傾きはゼロに等しい)
- H A : β 1 ≠ 0 (傾きはゼロではありません)
次に、次のように検定統計量を計算します。
t = b / SE b
金:
- b :係数の推定
- SE b : 係数推定値の標準誤差
tに対応する p 値が特定のしきい値 (例: α = 0.05) を下回る場合、帰無仮説は棄却され、予測変数と応答変数の間に統計的に有意な関係があると結論付けられます。
次の例は、実際に線形回帰モデルの t 検定を実行する方法を示しています。
例: 線形回帰の t 検定の実行
教授が 40 人の学生の学習時間と試験の成績との関係を分析したいとします。
学習時間を予測変数として、受け取った試験のスコアを応答変数として使用して、単純な線形回帰を実行します。
次の表は、回帰モデルの結果を示しています。
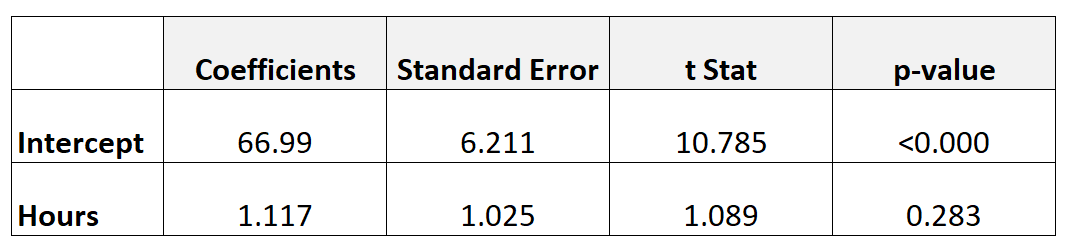
学習時間が最終試験の成績と統計的に有意な関係があるかどうかを判断するには、t 検定を実行できます。
この t 検定には次の帰無仮説と対立仮説を使用します。
- H 0 : β 1 = 0 (研究時間の傾きはゼロに等しい)
- H A : β 1 ≠ 0 (学習時間の傾きはゼロに等しくない)
次に、次のように検定統計量を計算します。
- t = b / SE b
- t = 1.117 / 1.025
- t = 1.089
df = n-2 = 40 – 2 = 38 でt = 1.089 に対応する p 値は0.283です。
T スコアから P 値への計算ツールを使用して、この p 値を計算することもできることに注意してください。

この p 値は 0.05 未満ではないため、帰無仮説を棄却できません。
これは、勉強時間と最終試験の結果の間に統計的に有意な関係がないことを意味します。
追加リソース
次のチュートリアルでは、線形回帰に関する追加情報を提供します。