Ti-84 電卓で二次回帰を実行する方法
2 つの変数に線形関係がある場合、多くの場合、 単純な線形回帰を使用してそれらの関係を定量化できます。

ただし、2 つの変数に二次関係がある場合は、二次回帰を使用してそれらの関係を定量化できます。

このチュートリアルでは、TI-84 計算機で二次回帰を実行する方法を説明します。
例: TI-84 計算機での二次回帰
労働時間と幸福度の関係を理解したいとします。 11 人の異なる人々の週の労働時間数と報告された幸福度 (0 から 100 のスケール) に関する次のデータがあります。

TI-84 計算機で二次回帰を実行するには、次の手順に従います。
ステップ 1: データを視覚化します。
二次回帰を使用する前に、説明変数 (時間) と応答変数 (幸福度) の関係が実際に二次であることを確認する必要があります。
まずは説明変数と応答変数のデータ値を入力します。 Statを押してからEDITを押します。 L1 列に説明変数 (労働時間) の次の値を入力し、L2 列に応答変数 (幸福度) の値を入力します。
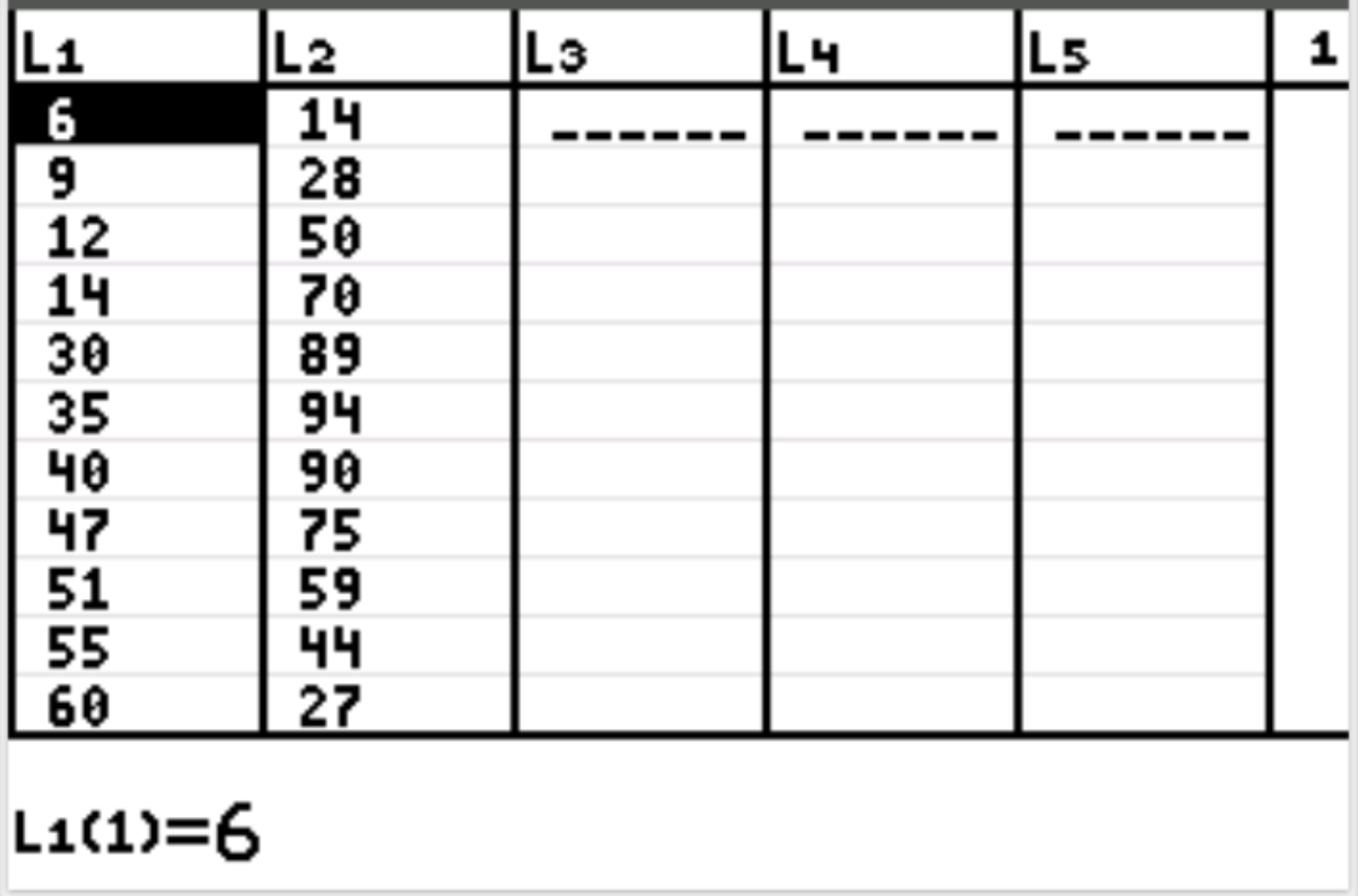
次に、 2nd を押してからy=を押して、 statplotメニューにアクセスします。 Plot1 を強調表示し、 Enterを押します。プロットが有効になっていて、Xlist と Ylist にそれぞれ L1 と L2 が選択されていることを確認します。
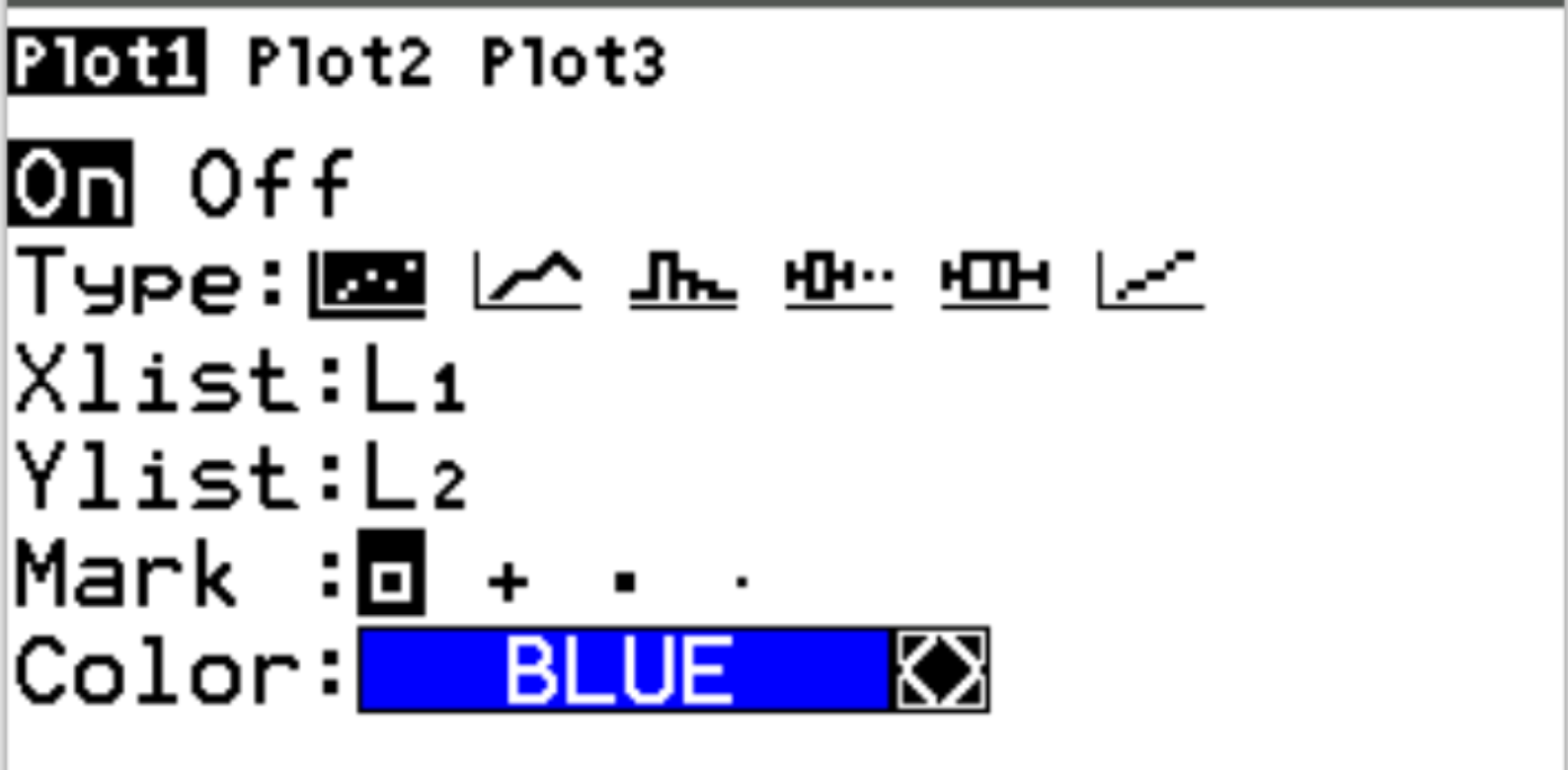
次に、ズームを押してから、 9:ZoomStatを押します。これにより、次の点群が自動的に生成されます。

労働時間がゼロからある時点まで増加すると幸福度は増加する傾向にありますが、労働時間がさらに増加すると幸福度は減少し始めることがわかります。
散布図のこの逆「U」字形は、労働時間と幸福度の間に 2 次の関係があることを示しています。つまり、この関係を定量化するには 2 次回帰を使用する必要があります。
ステップ 2: 二次回帰を実行します。
次に、二次回帰を実行します。 「Stat」を押してから「CALC」までスクロールします。次に、 「5:QuadReg」までスクロールしてEnterを押します。
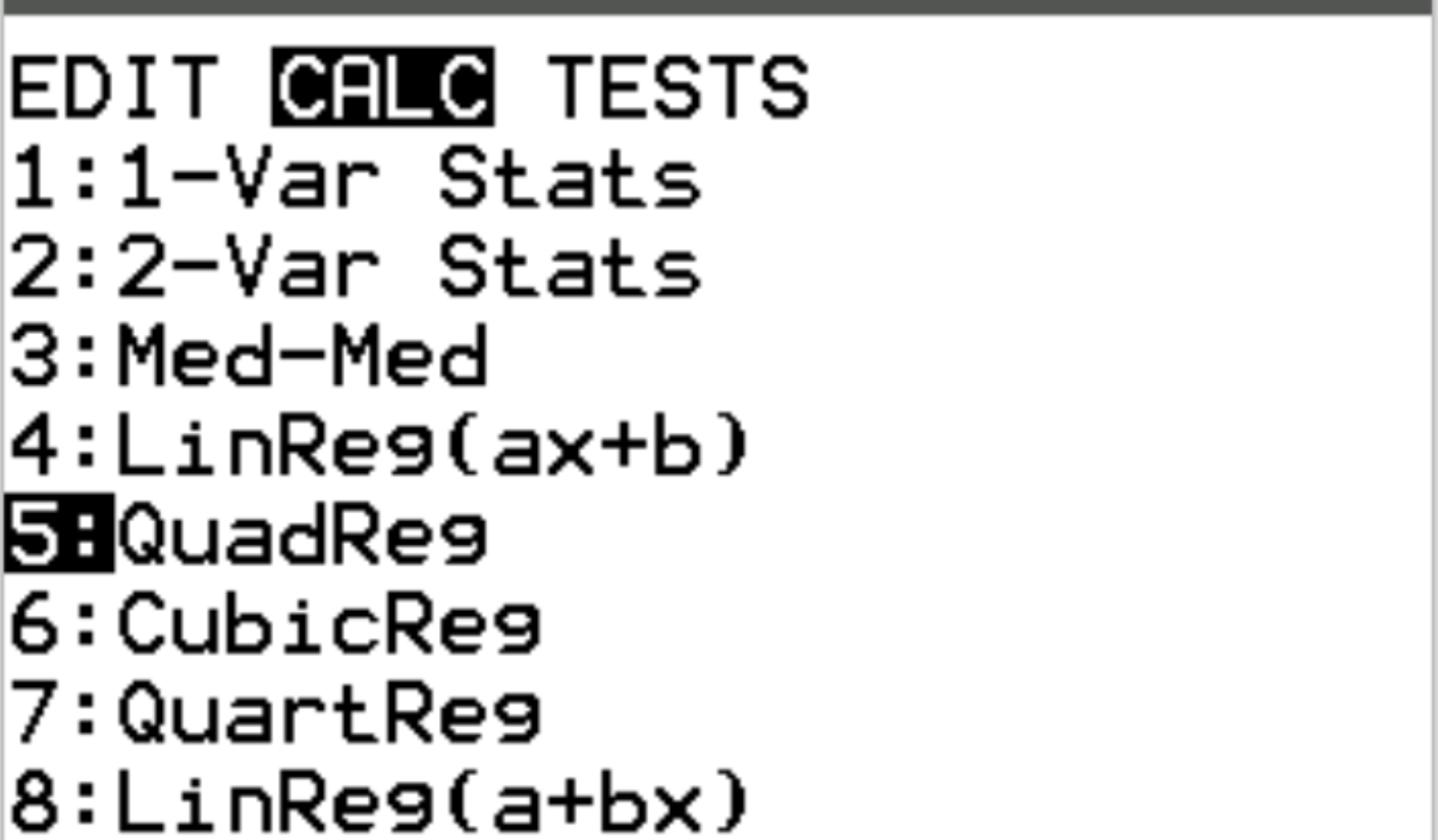
Xlist と Ylist については、データの入力に使用した列である L1 と L2 が選択されていることを確認してください。 FreqList は空のままにしておきます。 「計算」まで下にスクロールし、 Enterを押します。
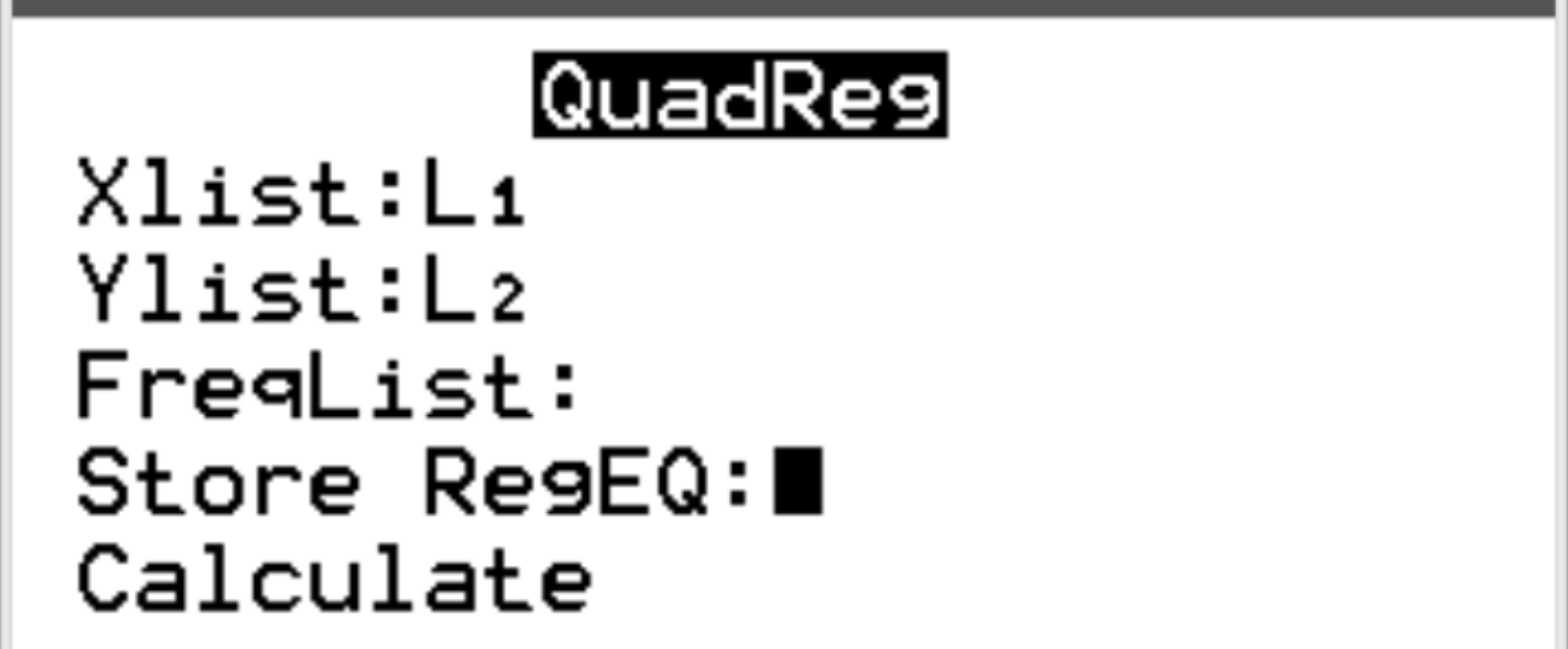
次の出力が自動的に表示されます。
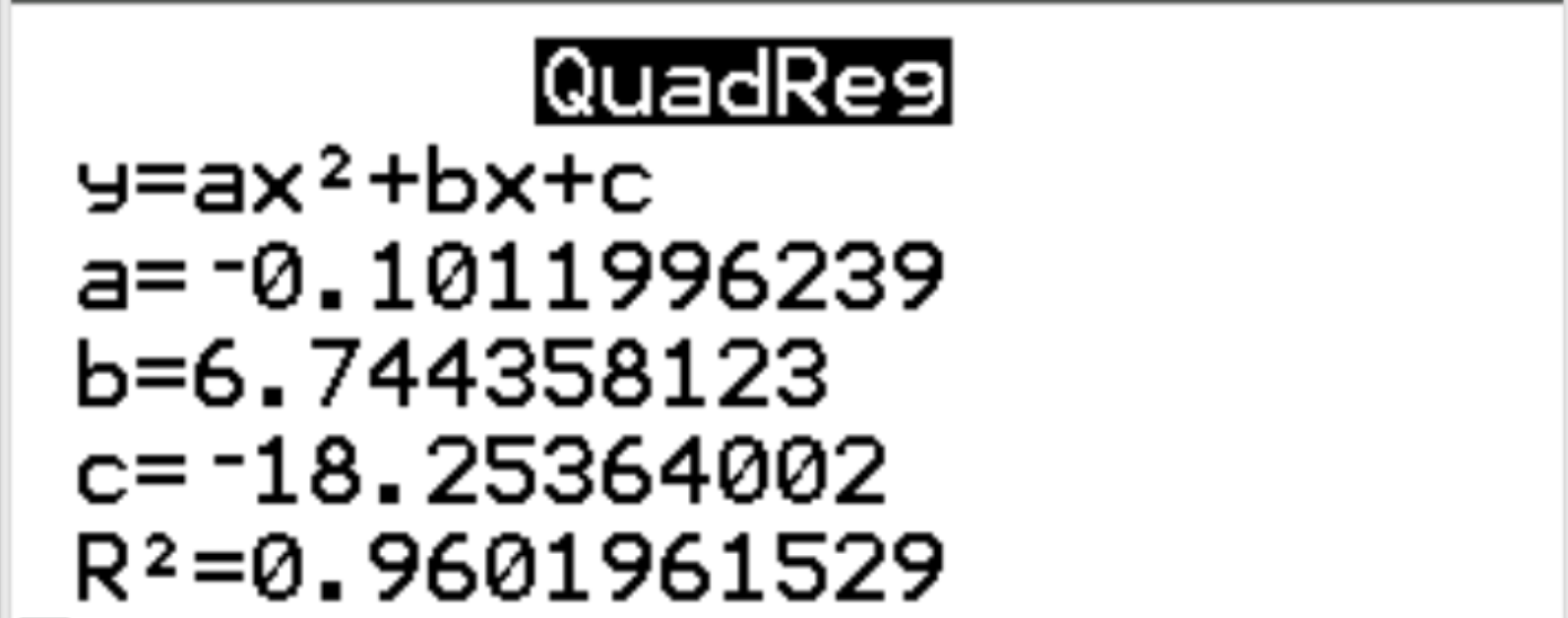
ステップ 3: 結果を解釈します。
結果から、推定された回帰式は次のとおりであることがわかります。
幸福度 = -0.1012 (時間) 2 + 6.7444 (時間) – 18.2536
この方程式を使用すると、週あたりの労働時間を考慮した個人の予測幸福度を見つけることができます。
たとえば、週に 60 時間働く人の幸福度は22.09になります。
幸福度 = -0.1012(60) 2 + 6.7444(60) – 18.2536 = 22.09
逆に、週に 30 時間働く人の幸福度は92.99になるはずです。
幸福度 = -0.1012(30) 2 + 6.7444(30) – 18.2536 = 92.99
回帰モデルの r の二乗が r 2 = 0.9602であることもわかります。これは、説明変数によって説明できる応答変数の分散の割合です。この例では、幸福度の変動の 96.02% は時間と回数で説明できます2 。