Excel で tukey-kramer 事後テストを実行する方法
一元配置分散分析は、 3 つ以上の独立したグループの平均間に統計的に有意な差があるかどうかを判断するために使用されます。
ANOVA で使用される仮定は次のとおりです。
帰無仮説 (H 0 ): µ 1 = µ 2 = µ 3 = … = µ k (平均は各グループで等しい)
対立仮説: (ハ): 少なくとも 1 つの手段が他の手段とは異なります。
ANOVA のp 値が有意水準を下回っている場合、帰無仮説を棄却し、グループ平均の少なくとも 1 つが他の平均とは異なると言える十分な証拠があると結論付けることができます。
ただし、これではどのグループが互いに異なるかはわかりません。これは単に、すべてのグループの平均が等しいわけではないことを示しています。どのグループが互いに異なっているかを正確に知るには、事後テストを実行する必要があります。
最も一般的に使用される事後検定は、グループの各ペアの組み合わせ間の平均を比較するTukey-Kramer 検定です。
次の例は、Excel で Tukey-Kramer テストを実行する方法を示しています。
例: Excel での Tukey-Kramer 検定
A、B、C の 3 つのグループに対して一元配置分散分析を実行するとします。一元配置分散分析の結果を以下に示します。
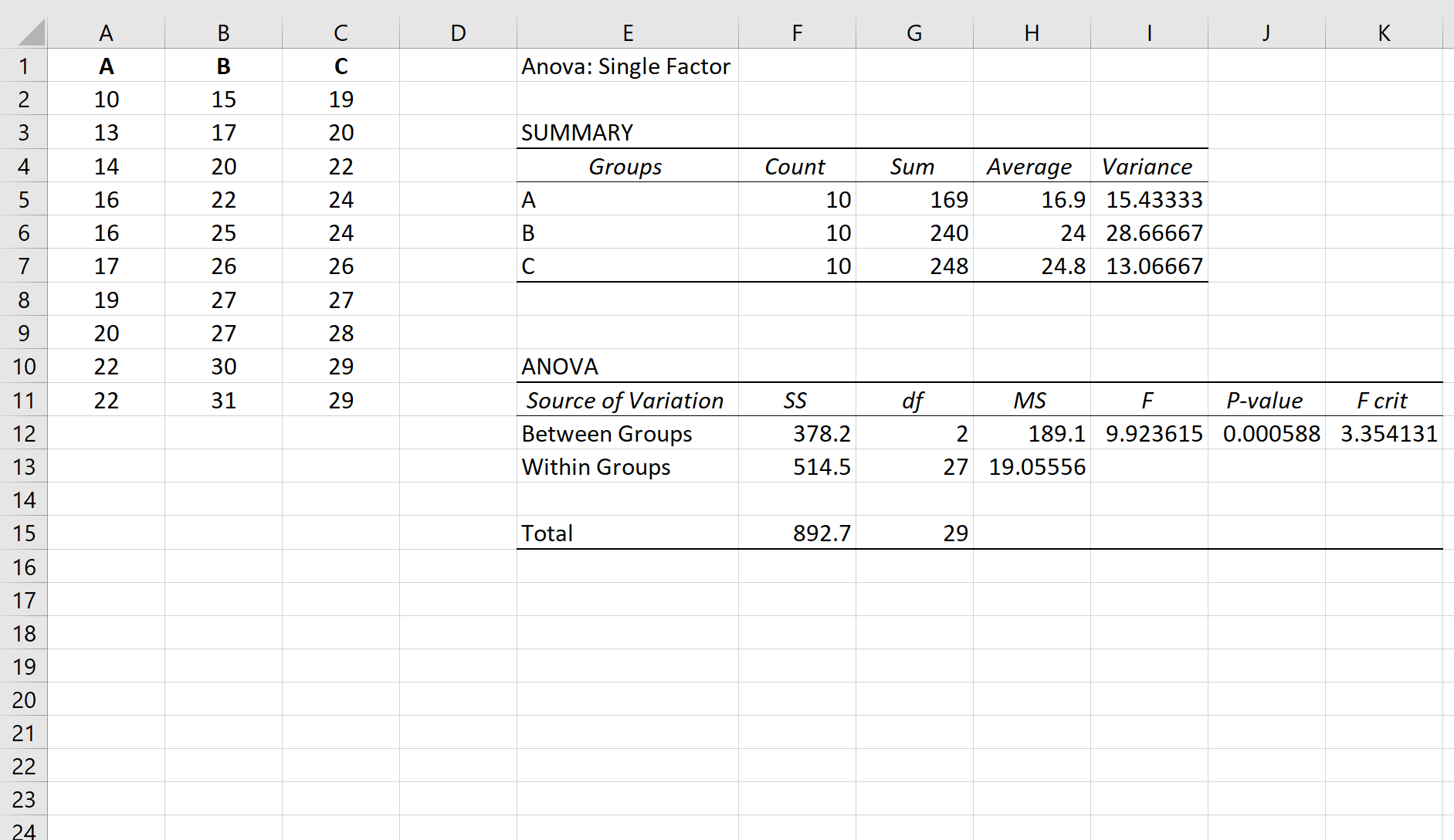
ANOVA テーブルの p 値は0.000588です。この p 値は 0.05 未満であるため、帰無仮説を棄却し、3 つのグループ間の平均は等しくないと結論付けることができます。
どのグループ平均が異なるかを正確に判断するには、次の手順を使用して Tukey-Kramer 事後検定を実行できます。
ステップ 1:各グループ間の絶対平均差を見つけます。
まず、ANOVA 結果の最初の表にリストされている平均を使用して、各グループ間の絶対平均差を見つけます。
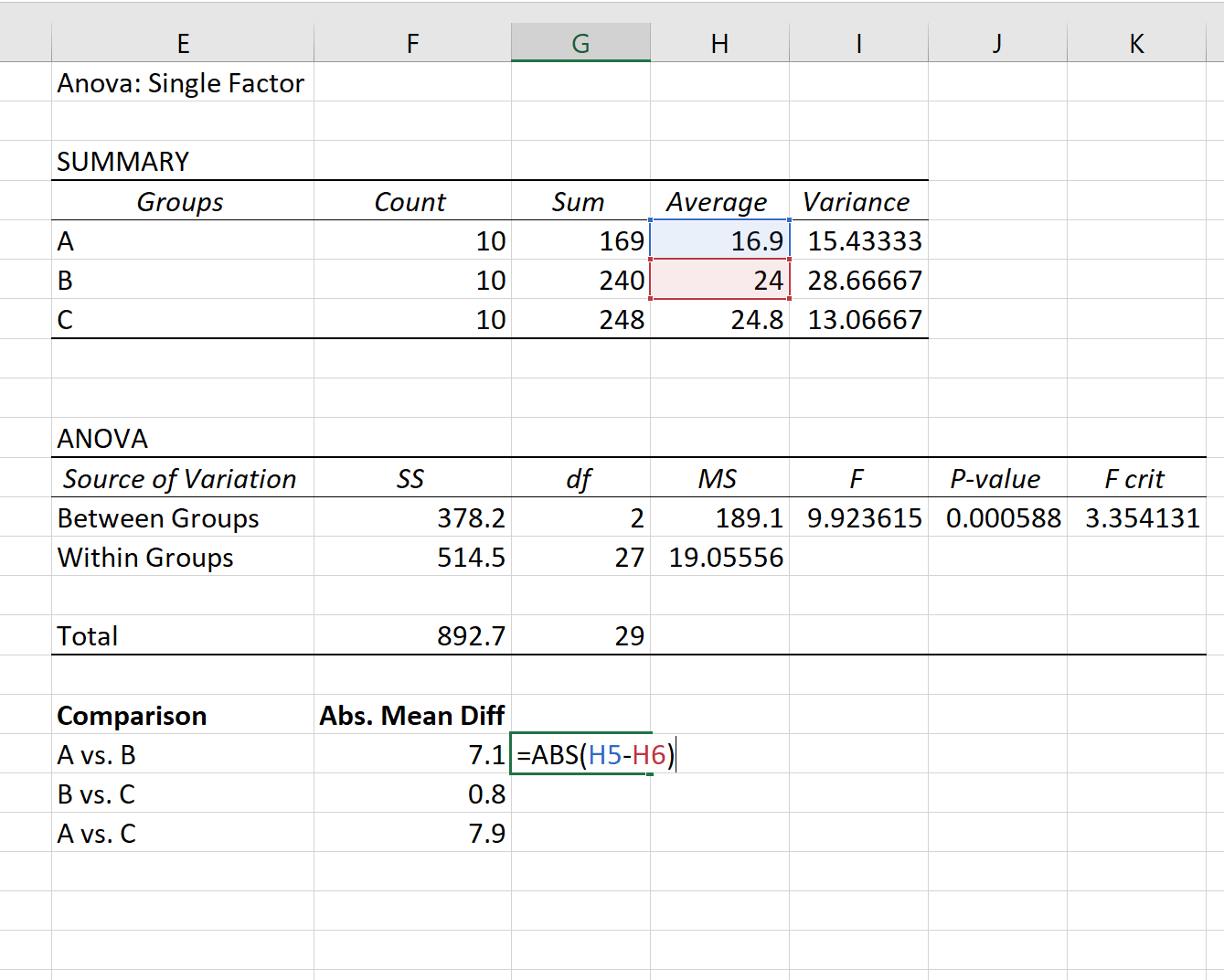
ステップ 2: Q の臨界値を見つけます。
次に、次の式を使用して Q の臨界値を見つける必要があります。
臨界値 Q = Q*√(s 2グループ化/ n.)
金:
- Q = Student Table Qの範囲の値
- s 2プール=すべてのグループにわたってプールされた分散
- ない。 = 特定のグループのサンプルサイズ
Q 値を見つけるには、次のようなスチューデント化範囲 Q テーブルを参照できます。
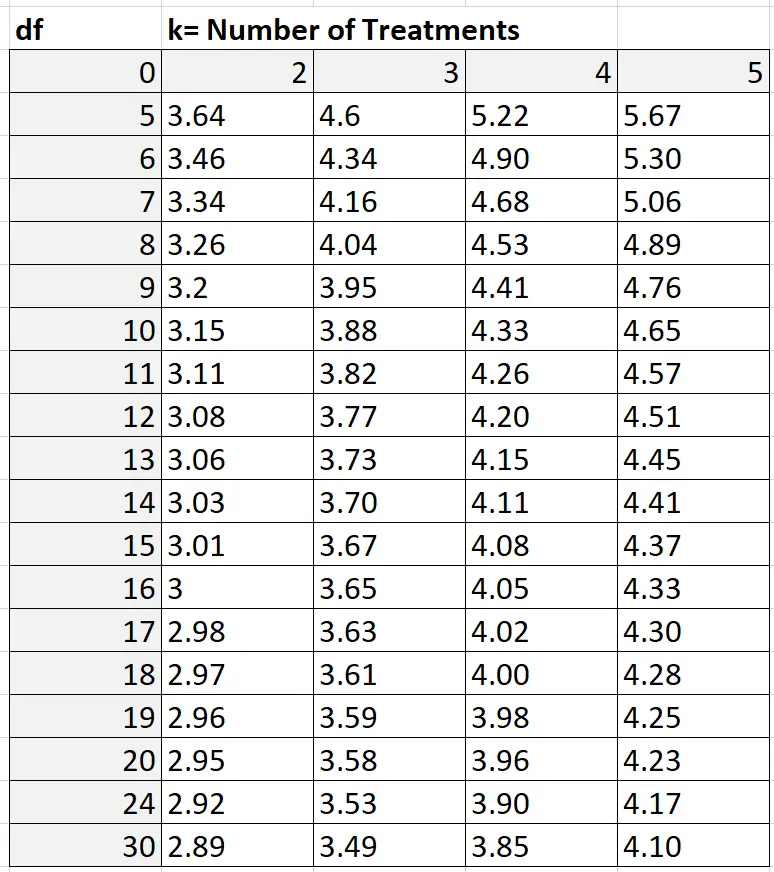
この例では、k = グループの数、つまり k = 3 です。自由度は次のように計算されます: nk = 30 – 3 = 27。27 は上の表に示されていないため、控えめな推定値 24 を使用できます。 k = 3 および df = 24 に基づいて、Q = 3.53であることがわかります。
プールされた分散はグループの分散の平均として計算でき、 19.056となります。
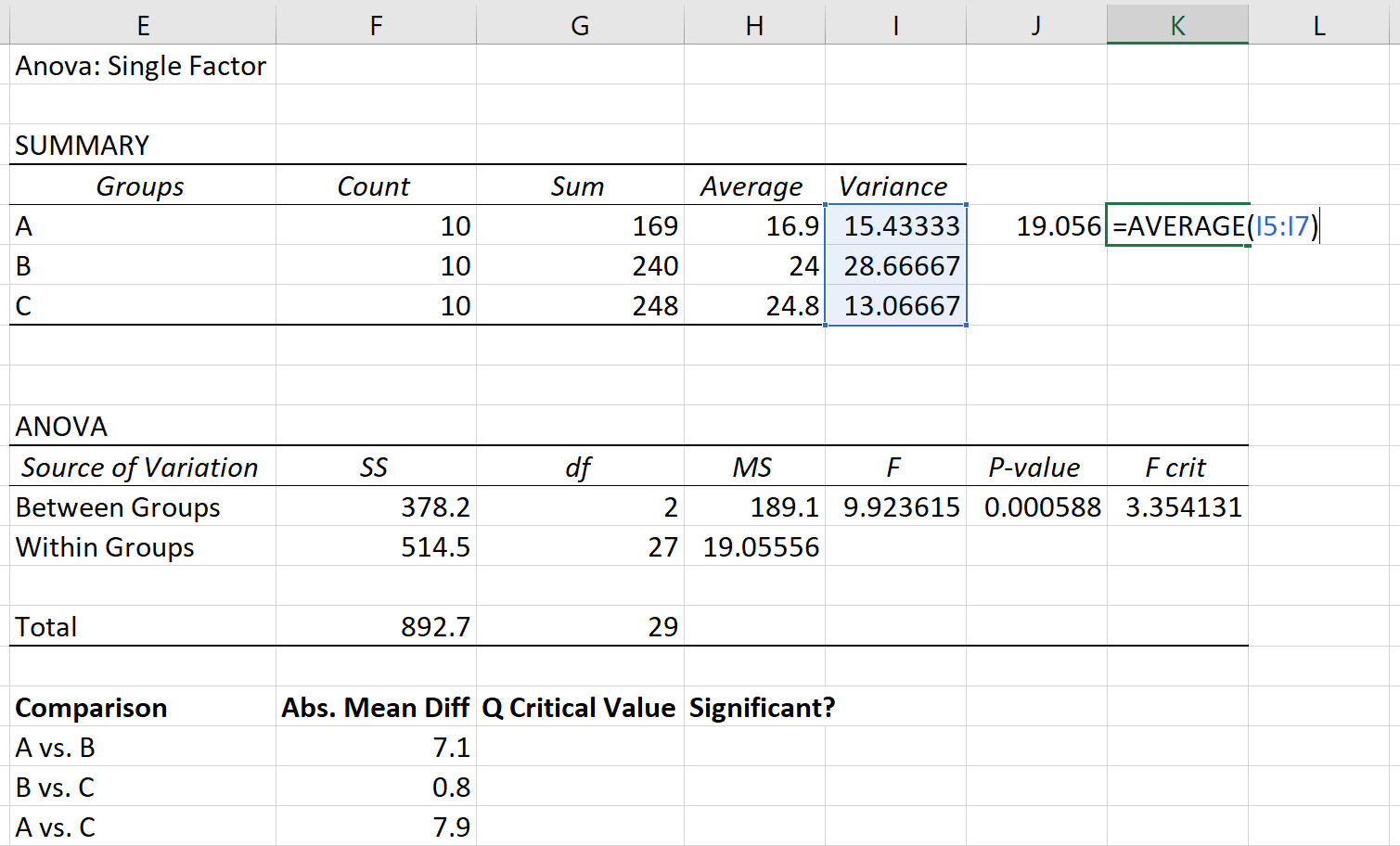
最後に、各グループのサンプルサイズは 10 です。
したがって、臨界値 Q は次のように計算できます。
臨界値 Q = Q*√(s 2 grouped / n.) = 3.53*√(19.056/10) = 4.87 。
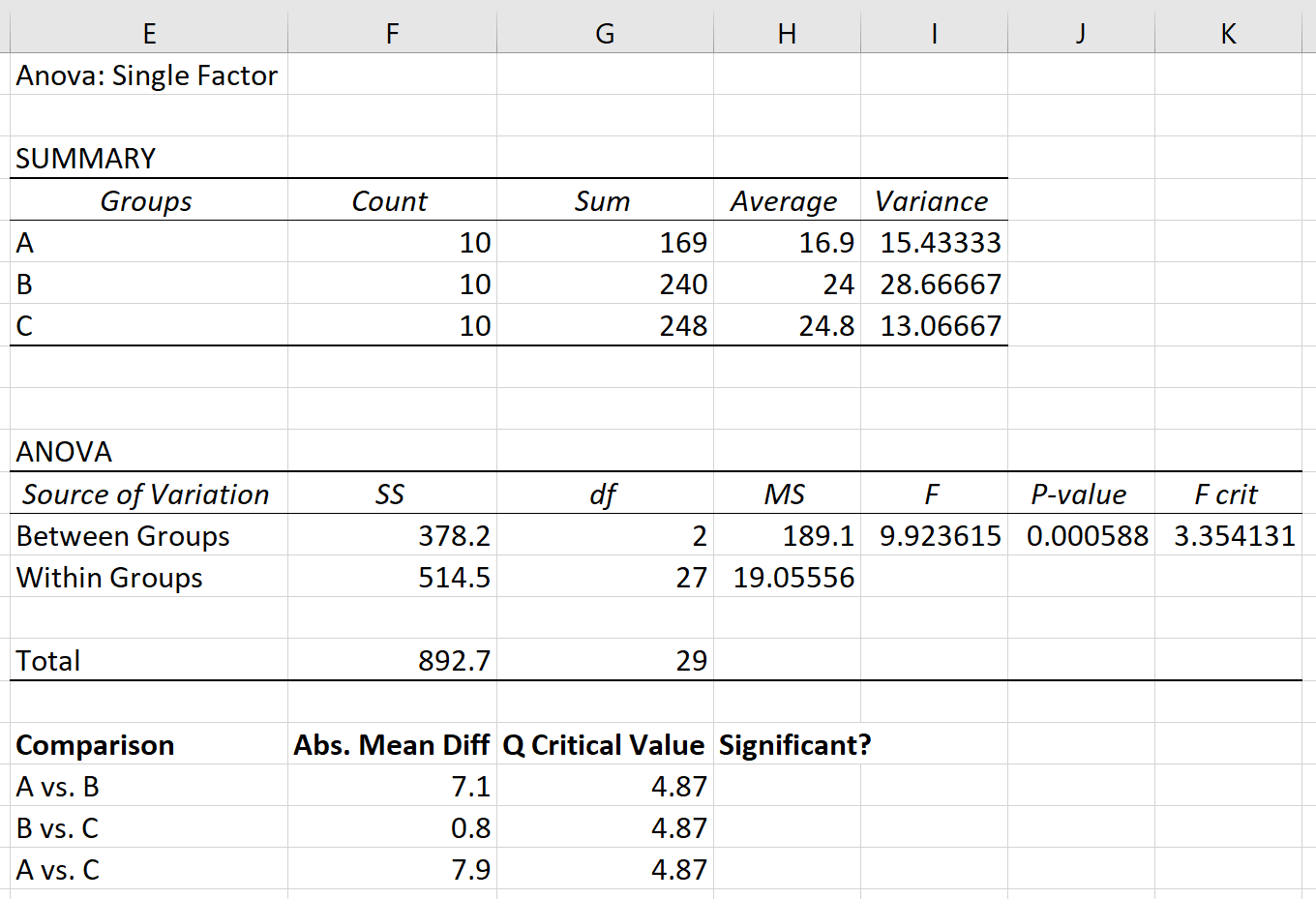
ステップ 3: どのグループの平均が異なるかを判断します。
最後に、各グループ間の絶対平均差を臨界値 Q と比較できます。絶対平均差が臨界値 Q より大きい場合、グループ平均間の差は統計的に有意です。
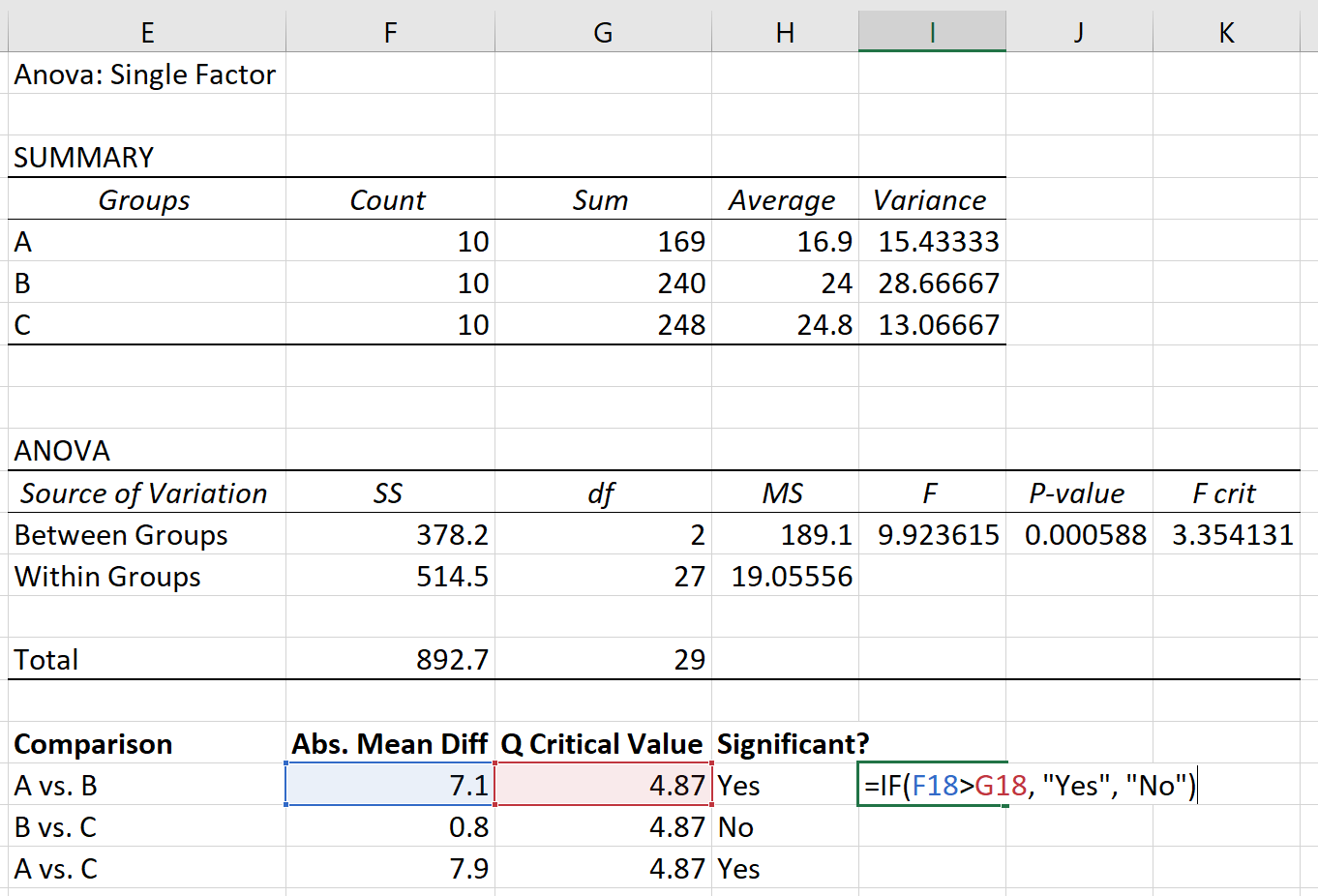
Tukey-Kramer 事後テストに基づいて、次のことがわかりました。
- グループ A とグループ B の間の平均の差は統計的に有意です。
- グループ B とグループ C の間の平均の差は統計的に有意ではありません。
- グループ A とグループ C の間の平均の差は統計的に有意です。