統計におけるt値とp値の違い
学生が統計学でよく混同する 2 つの用語は、t 値とp 値です。
これらの用語の違いを理解するには、 t 検定を理解することが役立ちます。
一般に、t 検定には 3 つの異なるタイプがあります。
- 1 サンプル t 検定: 母集団の平均が特定の値と等しいかどうかを検定するために使用されます。
- 2 標本 t 検定: 2 つの母集団の平均が等しいかどうかを検定するために使用されます。
- 対応のあるサンプルの t 検定: 一方のサンプルの各観測値がもう一方のサンプルの観測値と関連付けられる場合に、2 つの母集団の平均が等しいかどうかを検定するために使用されます。
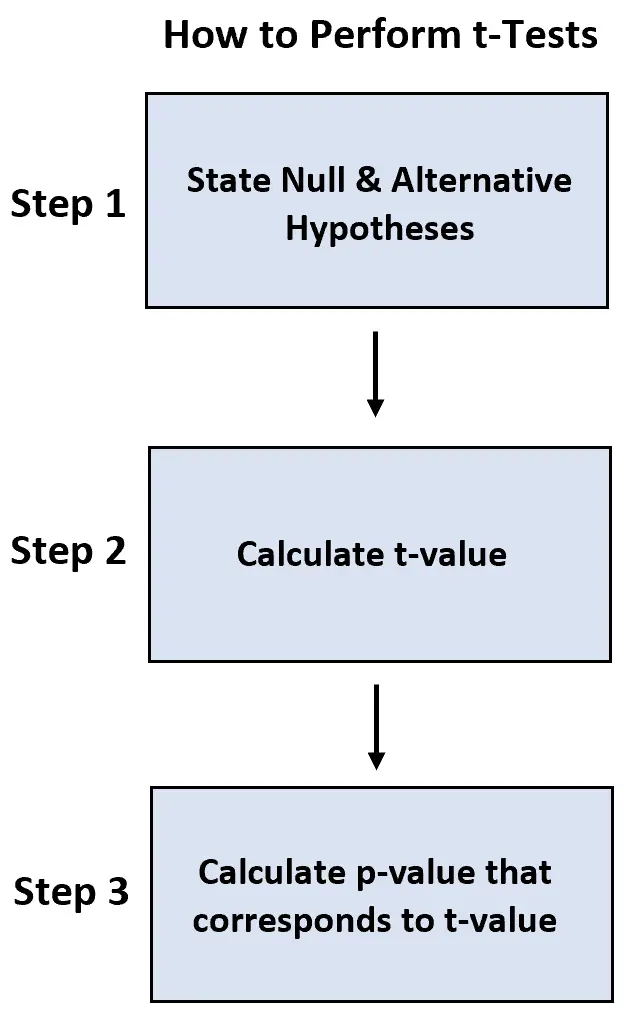
次の手順を使用して各テストを実行します。
- ステップ 1:帰無仮説と対立仮説を述べます。
- ステップ 2: t 値を計算します。
- ステップ 3: t 値に対応する p 値を計算します。
各検定について、 t 値は母平均の差を定量化する方法であり、 p 値はサンプルで実際に観察されたものと少なくとも同じ大きさの絶対値を持つ t 値が得られる確率です。帰無仮説が実際に正しい場合のデータ。
p 値が特定の値 (たとえば、0.05) より小さい場合、検定の帰無仮説は棄却されます。
t 検定の各タイプについて、 p 値に関心があり、単にt 値を中間ステップとして使用して p 値を計算します。
次の例は、2 サンプル t 検定の t 値と対応する p 値を計算して解釈する方法を示しています。
例: T 値と P 値の計算と解釈
2 つの異なる種のカメの平均体重が等しいかどうかを知りたいとします。次の重みを使用して、各母集団から 12 匹のカメの単純なランダム サンプルを収集します。
種 #1 : 301、298、295、297、304、305、309、298、291、299、293、304
種 #2 : 302、309、324、313、312、310、305、298、299、300、289、294
このデータを使用して 2 標本 t 検定を実行する方法は次のとおりです。
ステップ 1: 帰無仮説と対立仮説を述べます。
まず、帰無仮説と対立仮説を述べます。
- H 0 : μ 1 = μ 2 (2 つの母集団平均は等しい)
- H 1 : μ 1 ≠ μ 2 (2 つの母集団平均は等しくない)
ステップ 2: t 値を計算します。
次に、各カメ サンプルの重みを2 サンプル t 検定計算機に入力し、t 値が-1.608761であることを確認します。
ステップ 3: p 値を計算します。
2 サンプル t 検定計算ツールを使用して、t 値 -1.608761 に対応する p 値が0.121926であることを確認することもできます。
この p 値は 0.05 未満ではないため、帰無仮説を棄却できません。
これは、2 つの個体群間のカメの平均体重が異なると言える十分な証拠がないことを意味します。
p 値を計算するための中間ステップとして t 値を使用しただけであることに注意してください。 p 値は関心のある真の値ですが、最初に t 値を計算する必要がありました。
追加リソース
次のチュートリアルでは、t 検定と p 値に関する追加情報を提供します。
1 サンプル t 検定の概要
2 標本 t 検定の概要
対応のあるサンプルの t 検定の概要
t 検定から P 値を手動で計算する方法