Ti-84 カリキュレーターで重要な z 値を見つける方法
仮説検定を実行するたびに、検定統計量が得られます。仮説検定の結果が統計的に有意であるかどうかを判断するには、検定統計量を臨界 Z 値と比較します。検定統計量の絶対値が臨界 Z 値より大きい場合、検定結果は統計的に有意です。
TI-84 計算機で臨界値 Z を見つけるには、次の関数を使用できます。
invNorm(確率, μ, σ)
金:
- 確率:有意性のレベル
- μ:母集団平均
- σ:母集団標準偏差
TI-84 電卓でこの関数にアクセスするには、 2nd を押してからvarsを押します。これにより、 DISTR画面が表示され、そこでinvNorm()を使用できます。

このチュートリアルでは、TI-84 計算機で重要な Z 値を見つけるために invNorm() 関数を使用する例をいくつか紹介します。
例 1: 左側のテストの臨界値 Z
質問:有意水準 0.05 の左検定の臨界 Z 値を見つけます。
答え: invNorm(.05, 0, 1) = -1.6449
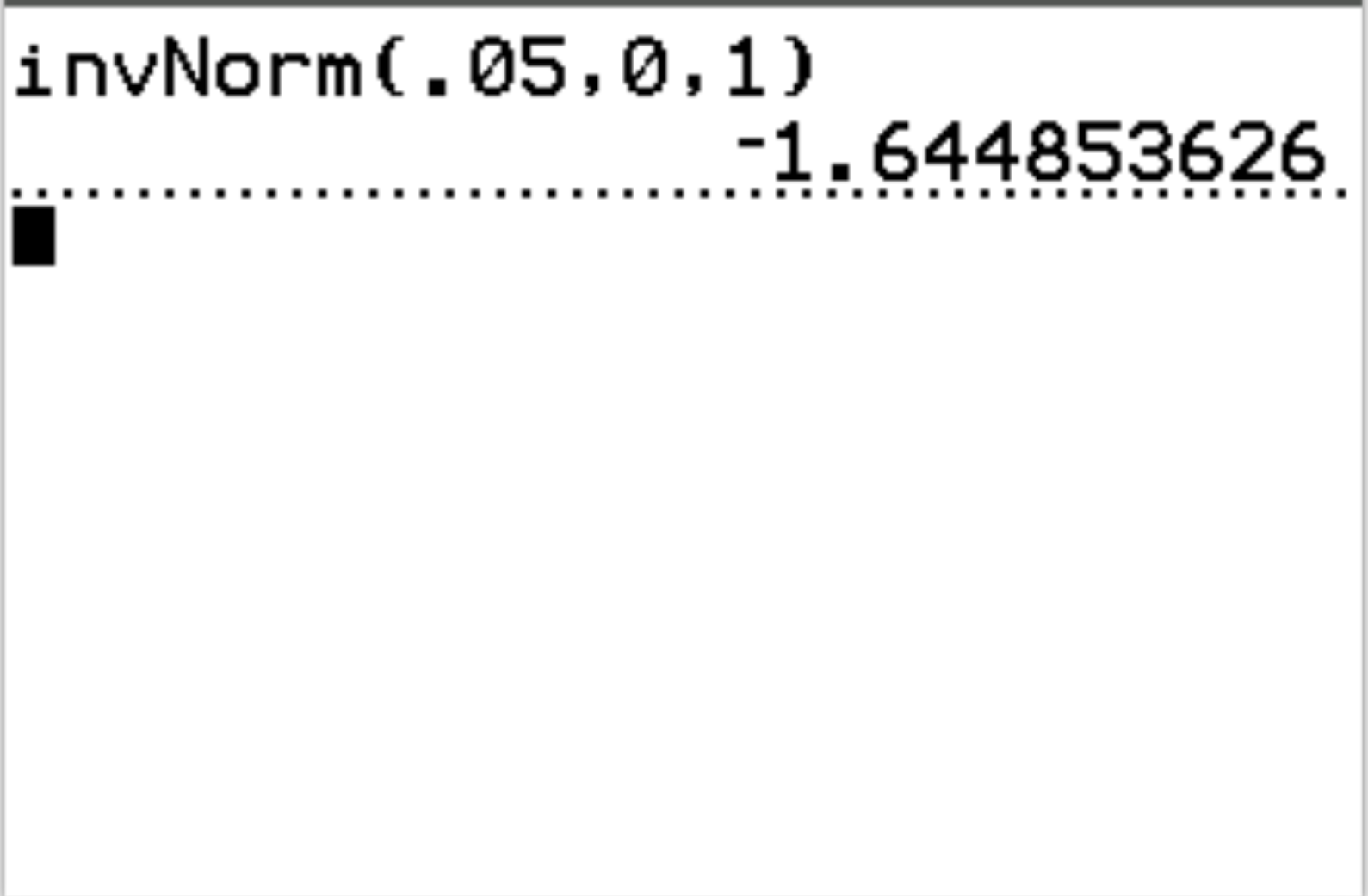
解釈:検定統計量が-1.6449未満の場合、検定結果は α = 0.05 で統計的に有意です。
例 2: ストレート テール テストの臨界 Z 値
質問:有意水準 0.10 の右側側面検定の臨界 Z 値を求めます。
答え: invT(1-.10, 0, 1) = 1.2816
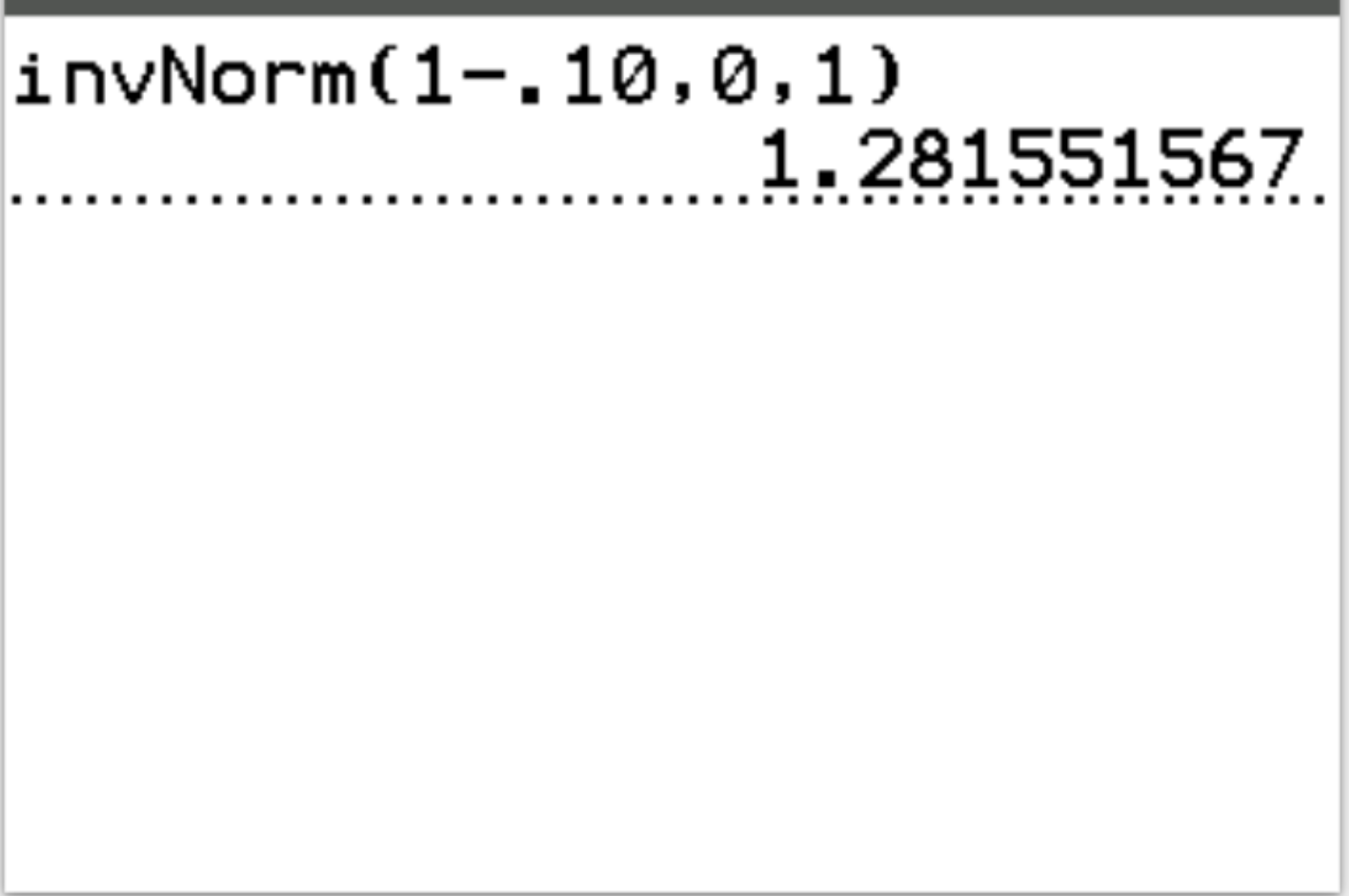
解釈:検定統計量が1.2816より大きい場合、検定結果は α = 0.10 で統計的に有意です。
例 3: 両側検定の臨界 Z 値
質問:有意水準 0.05 の両側検定の臨界 Z 値を見つけます。
答え: invNorm(.05/2, 0, 1) = -1.96, 1.96
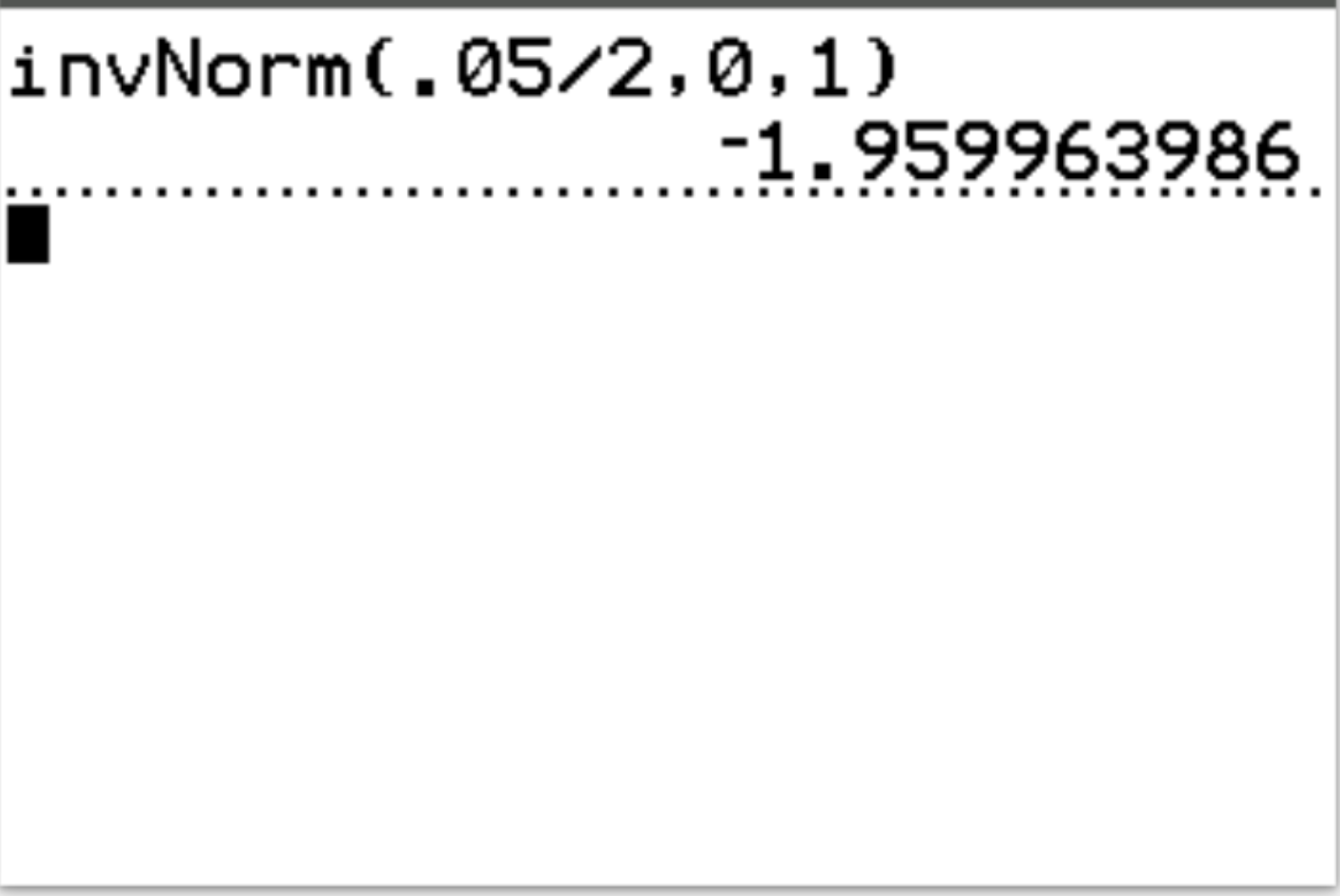
解釈:これは両側検定であるため、実際には-1.96と1.96という 2 つの臨界値があります。検定統計量が-1.96未満または1.96より大きい場合、検定結果は α = 0.05 で統計的に有意です。