Zテーブルの使い方(例付き)
Z テーブルは、標準正規分布における特定の Z スコアを下回る値の割合を示すテーブルです。
Z スコアは、個々のデータ値が平均からどれだけ標準偏差離れているかを単純に示します。次のように計算されます。
z スコア = (x – μ) / σ
金:
- x:個別のデータ値
- μ:母集団平均
- σ:母集団標準偏差
このチュートリアルでは、z テーブルの使用例をいくつか示します。
例1
特定の大学入学試験の得点は、平均μ = 82、標準偏差 σ = 8 で正規分布します。試験の得点が 84 未満の学生はおよそ何パーセントですか?
ステップ 1: Z スコアを見つけます。
まず、試験スコア 84 に関連付けられた Z スコアを見つけます。
z スコア = (x – μ) / σ = (84 – 82) / 8 = 2/8 = 0.25
ステップ 2: Z チャートを使用して、Z スコアに対応するパーセンテージを見つけます。
次に、z テーブルで値0.25を探します。

この試験では、約59.87%の生徒の得点が 84 点未満です。
例 2
特定の庭の植物の高さは、平均 μ = 26.5 インチ、標準偏差 σ = 2.5 インチで正規分布します。高さ 26 インチを超える植物はおよそ何パーセントですか?
ステップ 1: Z スコアを見つけます。
まず、高さ 26 インチに関連付けられた Z スコアを見つけます。
z スコア = (x – μ) / σ = (26 – 26.5) / 2.5 = -0.5 / 2.5 = -0.2
ステップ 2: Z チャートを使用して、Z スコアに対応するパーセンテージを見つけます。
次に、値-0.2を探します。 表z:
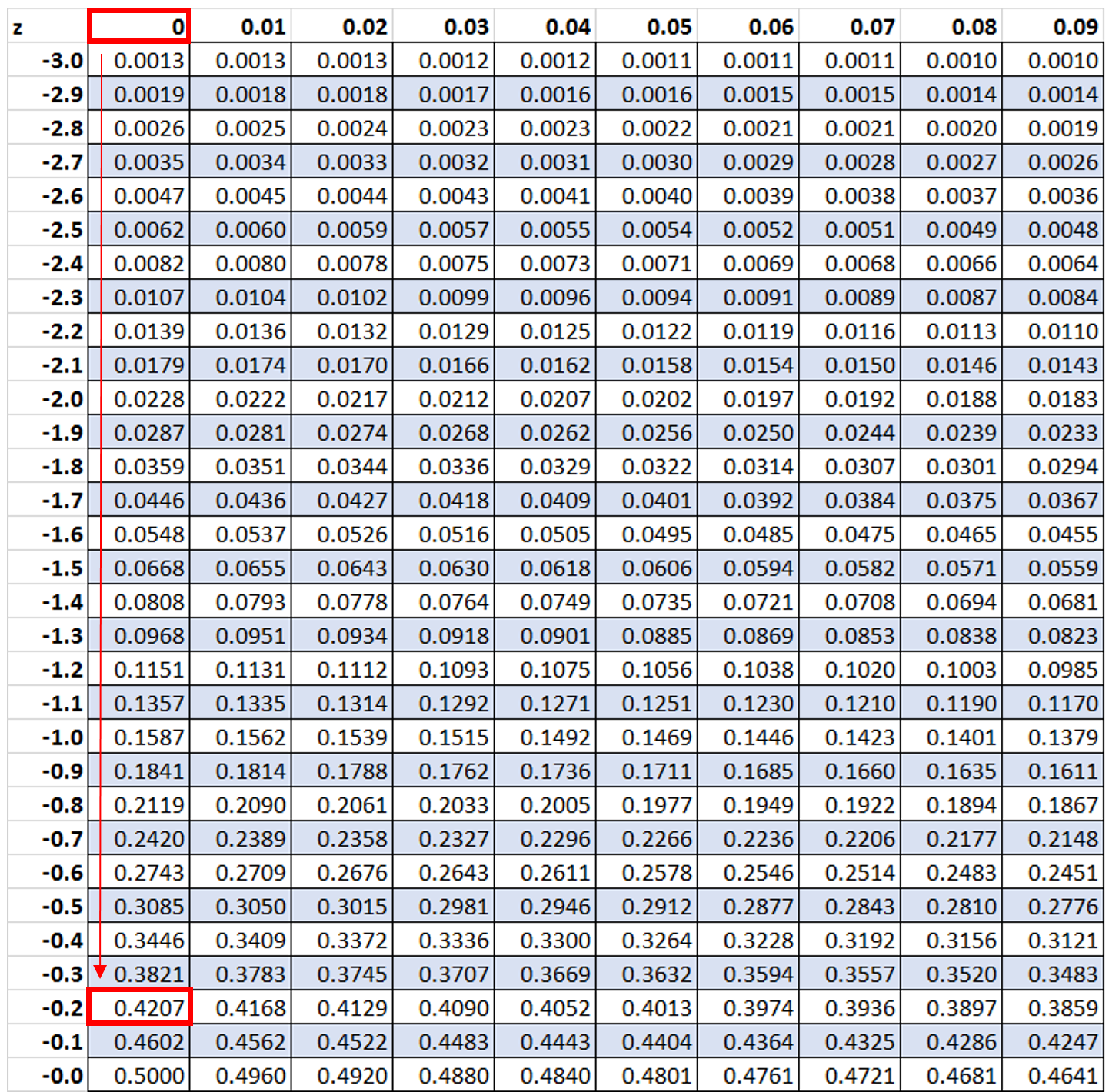
値の 42.07% が Z スコア -0.2 を下回っていることがわかります。ただし、この例では、-0.2より大きい値の割合を知りたいと考えています。これは、100% – 42.07% = 57.93% という式を使用して見つけることができます。
つまり、この庭園の植物の約59.87%は高さが 26 インチを超えています。
例 3
特定のイルカ種の体重は、平均μ = 400 ポンド、標準偏差 σ = 25 ポンドで正規分布します。体重が 410 ポンドから 425 ポンドの間のイルカはおよそ何パーセントですか?
ステップ 1: Z スコアを見つけます。
まず、410 冊と 425 冊の書籍に関連付けられた Z スコアを見つけます。
410 の Z スコア = (x – μ) / σ = (410 – 400) / 25 = 10/25 = 0.4
z スコア 425 = (x – μ) / σ = (425 – 400) / 25 = 25 / 25 = 1
ステップ 2: Z チャートを使用して、各 Z スコアに対応するパーセンテージを見つけます。
まず、値0.4を探します。 表z:

次に値1を探します。 表z:

最後に、最大値から最小値を引きます: 0.8413 – 0.6554 = 0.1859 。
つまり、イルカの約18.59%の体重は 410 ~ 425 ポンドです。