Z スコアから確率を求める方法: 例付き
Z スコアから確率を見つける最も簡単な方法は、Z テーブル内の Z スコアに対応する確率を単純に見つけることです。
このチュートリアルでは、z テーブルを使用して次の確率を見つける方法について説明します。
- 値が特定の Z スコアを下回る確率。
- 値が特定の Z スコアより大きい確率。
- 値が 2 つの特定の Z スコアの間に収まる確率。
さあ行こう!
例 1: 特定の Z スコア未満の確率
指定された分布内の値の z スコアがz = 0.25未満である確率を見つけたいとします。
この確率を見つけるには、z テーブルで 0.25 を探す必要があります。

特定の分布内の値の Z スコアがz = 0.25未満である確率は、約0.5987です。
注: これは、パーセンテージで59.87%と書くこともできます。
例 2: 特定の Z スコアを超える確率
指定された分布内の値の z スコアがz = -0.5より大きい確率を見つけたいとします。
この確率を見つけるには、z テーブルで -0.5 を探す必要があります。
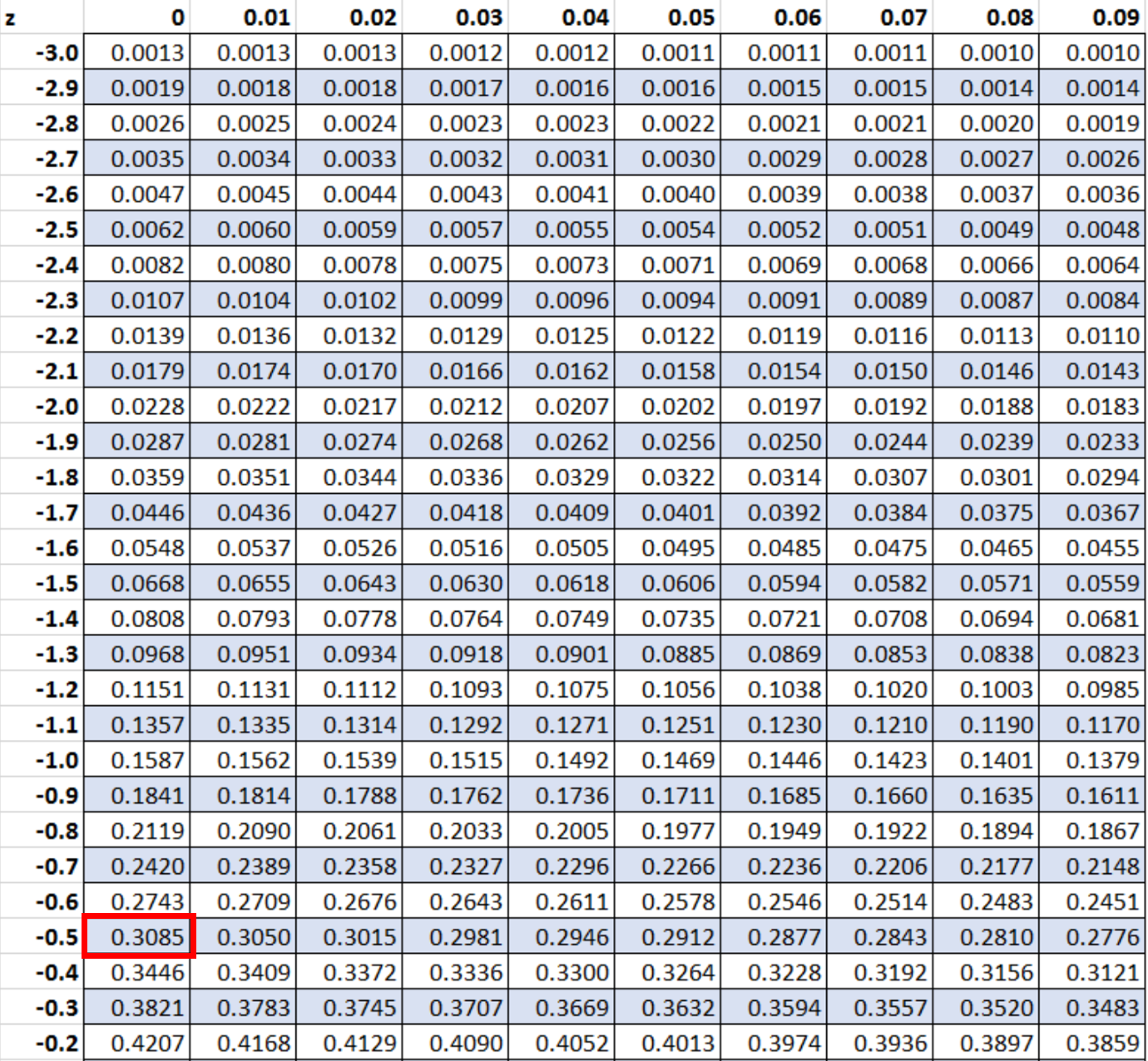
Z スコア -0.5 に対応する確率は 0.3085 です。
ただし、特定の分布内の値の Z スコアが -0.5より大きい確率を知りたいため、その確率を 1 から引く必要があります。
したがって、特定の分布内の値の Z スコアが -0.5 より大きい確率は、 1 – 0.3085 = 0.6915となります。
例 3: 2 つの Z スコア間の確率
指定された分布内の値の z スコアがz = 0.4とz = 1の間である確率を見つけたいとします。
まず、値0.4を探します。 表z:

次に値1を探します。 表z:

次に、大きい値から小さい値を引きます: 0.8413 – 0.6554 = 0.1859 。
したがって、特定の分布内の値の z スコアが z = 0.4 と z = 1 の間である確率は、約0.1859です。
追加リソース
次のチュートリアルでは、Z スコアに関する追加情報を提供します。