Z スコアがマイナスになることはありますか?
統計では、 Z スコアは、値が平均からどれだけ標準偏差があるかを示します。次の式を使用して Z スコアを計算します。
z = (X – μ) / σ
ここで、X は分析する値、μ は平均、σ は標準偏差です。
z スコアは、正、負、またはゼロのいずれかになります。
正の Z スコアは特定の値が平均より高いことを示し、負の Z スコアは特定の値が平均より低いことを示し、ゼロの Z スコアは特定の値が平均と等しいことを示します。
いくつかの例を見れば、これが明らかになるはずです。
例: Z スコアの計算
特定の植物グループの高さ (インチ単位) を示す次のデータセットがあるとします。
5、7、7、8、9、10、13、17、17、18、19、19、20
このデータセットのサンプル平均は13 、サンプル標準偏差は5.51です。
1. このデータセット内の値「8」の Z スコアを見つけます。
Z スコアを計算する方法は次のとおりです。
z = (X – μ) / σ = (8 – 13) / 5.51 = -0.91
これは、値「8」が平均よりも 0.91 標準偏差低いことを意味します。
2. このデータセット内の値「13」の Z スコアを見つけます。
Z スコアを計算する方法は次のとおりです。
z = (X – μ) / σ = (13 – 13) / 5.46 = 0
これは、値「13」が平均と正確に等しいことを意味します。
3. このデータセット内の値「20」の Z スコアを見つけます。
Z スコアを計算する方法は次のとおりです。
z = (X – μ) / σ = (20 – 13) / 5.46 = 1.28
これは、値「20」が平均より1.28 標準偏差高いことを意味します。
Z スコアの解釈方法
AZ チャートは、特定の Z スコアを下回る値の割合を示します。いくつかの例を見れば、これが明らかになるはずです。
例 1: 負の Z スコア
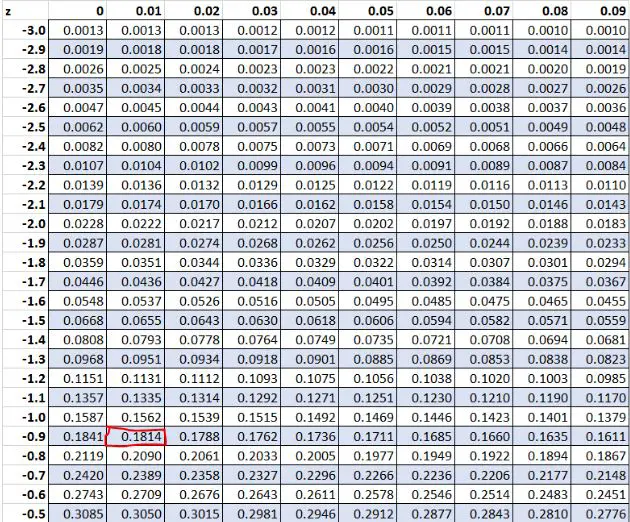
先ほど、データセット内の生の値「8」の Z スコアが-0.91であることがわかりました。 Z テーブルによると、18.14% の値がこの値より低くなります。
例 2: Z スコアがゼロに等しい
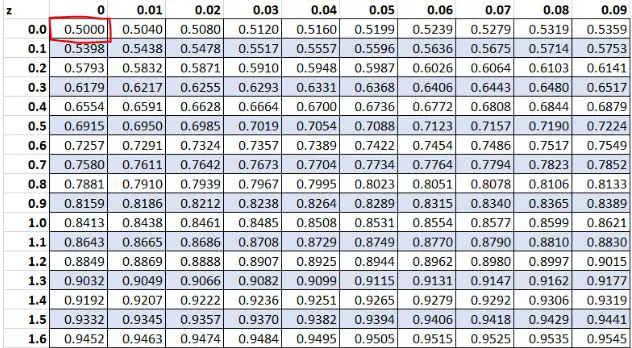
先ほど、データセット内の生の値「13」の Z スコアが0であることがわかりました。 Z テーブルによると、50.00% の値がこの値未満です。
例 3: 正の Z スコア
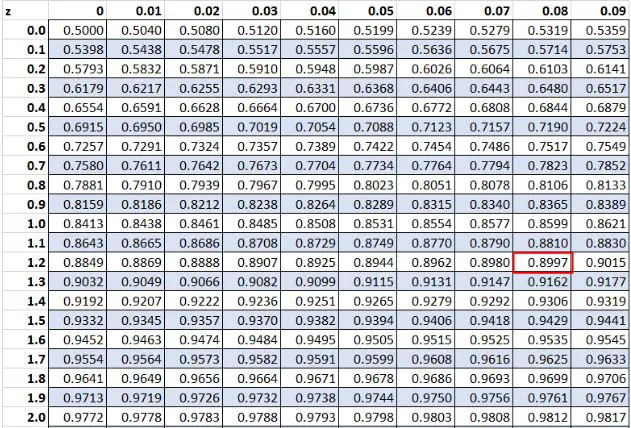
先ほど、データセット内の生の値「20」の Z スコアが1.28であることがわかりました。 Z テーブルによると、89.97% の値がこの値より低くなります。
結論
Z スコアは負の無限大と正の無限大の間の任意の値を取ることができますが、ほとんどの Z スコアは平均の 2 標準偏差以内にあります。実際、統計には経験則として知られるルールがあり、正規分布を持つ特定のデータセットについて次のように述べられています。
- データ値の68% は平均値の 1 標準偏差以内にあります。
- データ値の95% は平均値の 2 標準偏差以内にあります。
- データ値の99.7% が平均値の 3 標準偏差以内に収まります。
Z スコアの絶対値が高いほど、生の値がデータセットの平均から遠くなります。 Z スコアの絶対値が低いほど、生の値はデータセットの平均に近づきます。
関連トピック: