Z スコア正規化: 定義と例

Z スコア正規化とは、すべての値の平均が 0、標準偏差が 1 になるように、データセット内の各値を正規化するプロセスを指します。

次の式を使用して、データセット内の各値に対して Z スコア正規化を実行します。

新しい値 = (x – μ) / σ

金：

• x : 元の値
• μ : データの平均値
• σ : データの標準偏差

次の例は、実際にデータセットに対して Z スコア正規化を実行する方法を示しています。

例: Z スコア正規化の実行

次のデータセットがあるとします。

計算機を使用すると、データセットの平均は21.2 、標準偏差は29.8であることがわかります。

データセットの最初の値に対して Z スコア正規化を実行するには、次の式を使用できます。

• 新しい値 = (x – μ) / σ
• 新しい値 = (3 – 21.2) / 29.8
• 新しい値 = -0.61

この式を使用して、データセット内の各値に対して Z スコア正規化を実行できます。

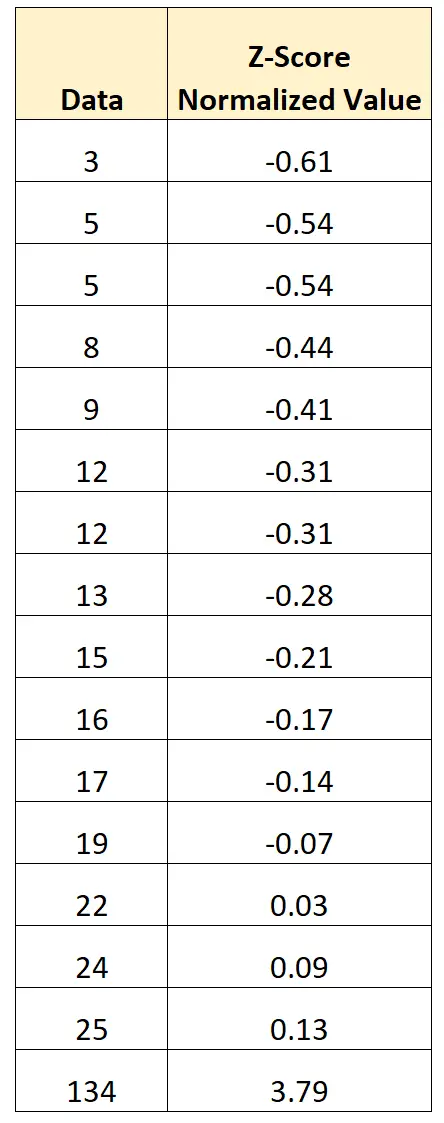
正規化された値の平均は0で、正規化された値の標準偏差は1です。

正規化された値は、元の値と平均の間の標準偏差の数を表します。

例えば：

• データセットの最初の値は、平均より0.61標準偏差下です。
• データセットの 2 番目の値は、平均より0.54標準偏差低いです。
• …
• データセットの最後の値は、平均を3.79標準偏差上回っています。

このタイプの正規化を実行する利点は、データ セット (134) 内の明らかな外れ値が、もはや大規模な外れ値ではなくなるように変換されていることです。

このデータセットを使用して何らかのタイプの機械学習モデルを当てはめると、外れ値はモデルの当てはめに及ぼす影響を及ぼさなくなります。

追加リソース

次のチュートリアルでは、さまざまな正規化手法に関する追加情報を提供します。

標準化と正規化: 違いは何ですか?
データを0と1の間で正規化する方法
データを0から100の間で正規化する方法