Sas で z スコアを計算する方法
統計では、 Z スコアは、値が平均からどれだけ標準偏差があるかを示します。
次の式を使用して Z スコアを計算します。
z = (X – μ) / σ
金:
- X は単一の生データ値です
- μ はデータセットの平均です
- σ はデータセットの標準偏差です
次の例は、SAS で生データ値の Z スコアを計算する方法を示しています。
例: SAS での Z スコアの計算
SAS で次のデータセットを作成するとします。
/*create dataset*/ data original_data; input values; datalines ; 7 12 14 12 16 18 6 7 14 17 19 22 24 13 17 12 ; run ; /*view dataset*/ proc print data = original_data;
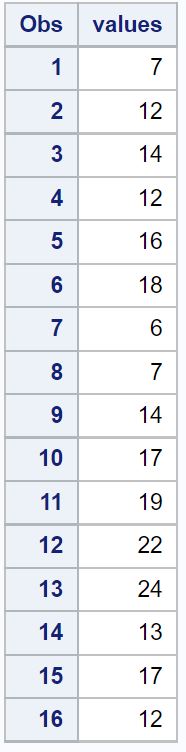
ここで、データセット内の各値の Z スコアを計算するとします。
proc sql を使用してこれを行うことができます。
/*create new variable that shows z-scores for each raw data value*/
proc sql ;
select values, (values - mean(values)) / std(values) as z_scores
from original_data;
quit ;
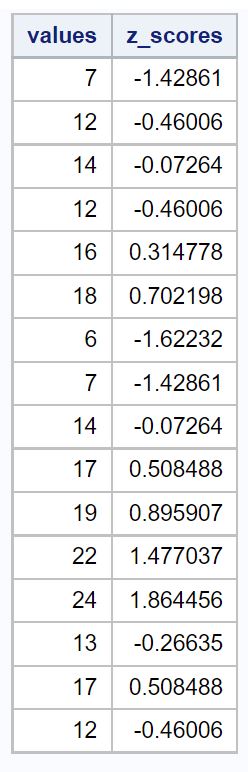
値列には元のデータ値が表示され、 z_scores列には各値の Z スコアが表示されます。
SAS で Z スコアを解釈する方法
Z スコアは、値が平均からどれだけ標準偏差があるかを示します。
z スコアは、正、負、またはゼロのいずれかになります。
正の Z スコアは特定の値が平均より高いことを示し、負の Z スコアは特定の値が平均より低いことを示し、ゼロの Z スコアは特定の値が平均と等しいことを示します。
データセットの平均と標準偏差を計算すると、平均は14.375 、標準偏差は5.162であることがわかります。
したがって、データセットの最初の値は 7 で、その Z スコアは (7-14.375) / 5.162 = -1.428でした。これは、値「7」が平均より 1.428 標準偏差低いことを意味します。
データの次の値 12 の Z スコアは (12-14.375) / 5.162 = -0.46でした。これは、値「12」が平均よりも 0.46 標準偏差低いことを意味します。
値が平均から離れるほど、その値の Z スコアの絶対値は大きくなります。
たとえば、値 7 は値 12 よりも平均 (14.375) から離れています。これは、7 の Z スコアの絶対値がより大きい理由を説明しています。
追加リソース
次の記事では、SAS で他の一般的なタスクを実行する方法について説明します。