Ti-84 電卓で z スコアからパーセンタイルを見つける方法
TI-84 計算機で Z スコアのパーセンタイルを見つけるには、次の構文を使用できます。
Normalcdf (-99、Z スコア、μ、σ)
金：
- μ = 母平均
- σ = 母標準偏差
TI-84 電卓でこの関数にアクセスするには、 2nd を押してからVARS を押し、 normalcdf までスクロールして (そしてENTERを押します) だけです。
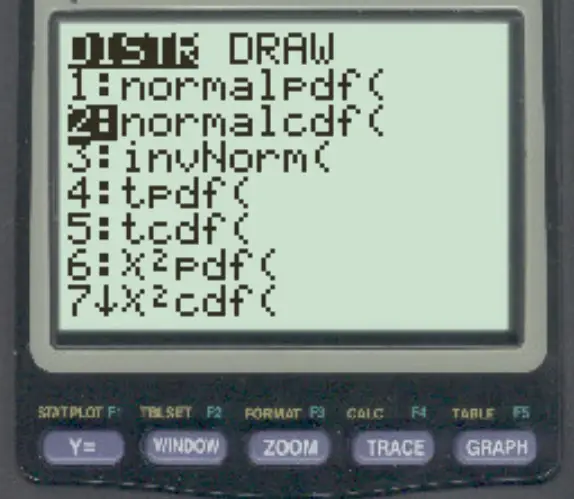
次の例は、この関数を実際に使用する方法を示しています。
例 1: 負の Z スコアのパーセンタイルを求める
-1.44の Z スコアに対応するパーセンタイルを見つけたいとします。
TI-84 計算機で次の構文を使用して、このパーセンタイルを見つけることができます。
normalcdf (-99, -1.44, 0, 1)
注:負の無限大の値をシミュレートするために、「下限」として -99 を使用します。
Z スコア -1.44 に対応するパーセンタイルは0.0749です。これは、正規分布内の値の 7.49% のみが Z スコア -1.44 を下回ることを意味します。
例 2: 正の Z スコアのパーセンタイルを求める
Z スコア0.56に対応するパーセンタイルを見つけたいとします。
TI-84 計算機で次の構文を使用して、このパーセンタイルを見つけることができます。
normalcdf (-99, 0.56, 0, 1)
ここでも、負の無限大の値をシミュレートするために、「下限」として -99 を使用します。
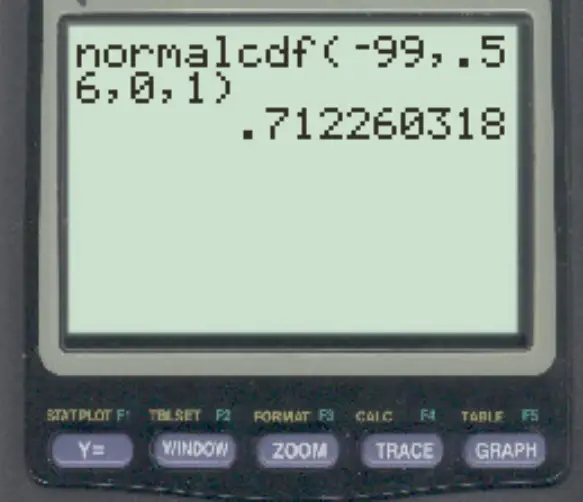
Z スコア 0.56 に対応するパーセンタイルは0.7123です。これは、正規分布の値の 71.23% が Z スコア 0.56 を下回っていることを意味します。
パーセンタイルと Z スコアの関係
Z スコアは、負の無限大から無限大までの任意の値を取ることができます。ただし、パーセンタイルは 0 から 100 までの値のみを取ることができます。
0 の Z スコアは、正確に 0.50 のパーセンタイルに対応します。したがって、0 より大きい Z スコアは 0.50 より大きいパーセンタイルに対応し、0 より小さい Z スコアは 0.50 より小さいパーセンタイルに対応します。
追加リソース
著者について
ベンジャミン・アンダーソン博士
私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。 統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る