さまざまな分布の z スコアの比較
Z スコアは、個々のデータ値が平均からどれだけ標準偏差離れているかを示します。次のように計算されます。
z スコア = (x – μ) / σ
金:
- x:個別のデータ値
- μ:母集団平均
- σ:母集団標準偏差
個々の値の Z スコアは次のように解釈できます。
- 正の Z スコア:個々の値が平均を上回っています。
- 負の Z スコア:個々の値が平均よりも低くなります。
- Z スコア 0:個々の値は平均と等しくなります。
Z スコアは、2 つの異なる分布からの 2 つのデータ ポイントの相対位置を比較する場合に特に役立ちます。これを説明するために、次の例を考えてみましょう。
例: Z スコアの比較
特定の大学の試験の得点は、平均 μ = 80、標準偏差 σ = 4 で正規分布します。デュアンはこの試験で 84 点を獲得しました。
別の大学の試験の得点は、平均 μ = 85、標準偏差 σ = 8 で正規分布します。デビーはその試験で 90 点を獲得しました。
自分の試験得点の分布と比較して、誰が試験で最高の結果を達成しましたか?
この質問に答えるために、各人の試験スコアの Z スコアを計算できます。
Duane の z スコア = (x – μ) / σ = (84 – 80) / 4 = 4 / 4 = 1
デビーの Z スコア = (x – μ) / σ = (90 – 85) / 8 = 5/8 = 0.625
デビー デュアンのスコアは高かったですが、実際には、特定の試験の分布と比較すると、デュアンのスコアの方が高かったです。
これを理解するには、状況を視覚化することが役立ちます。以下は、デュアンのスコアを彼の特定の試験の内訳と比較したものです:
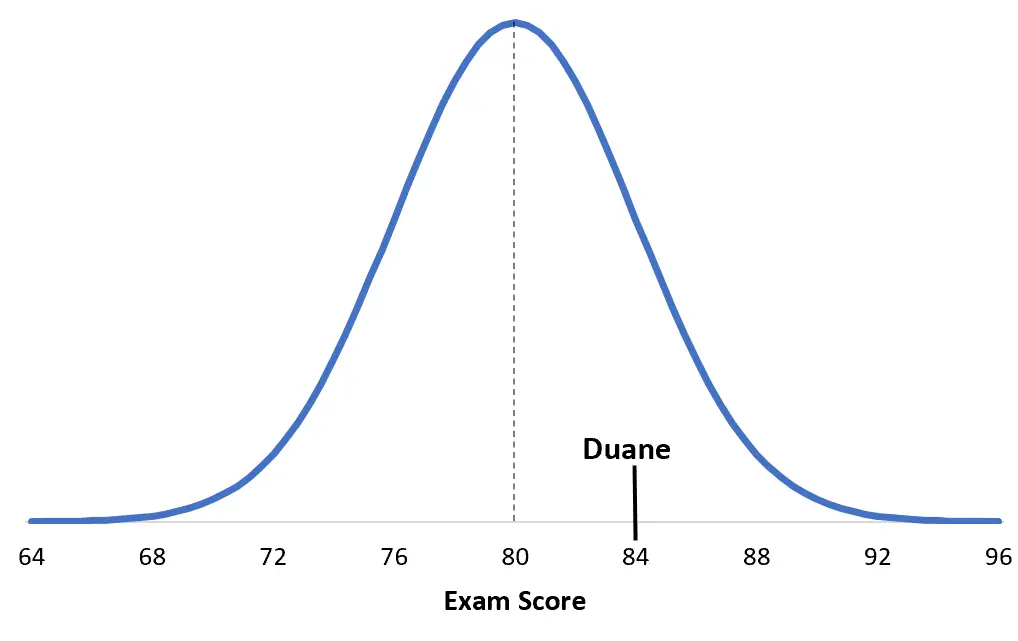
そして、これがデビーの試験の内訳からのスコアです。
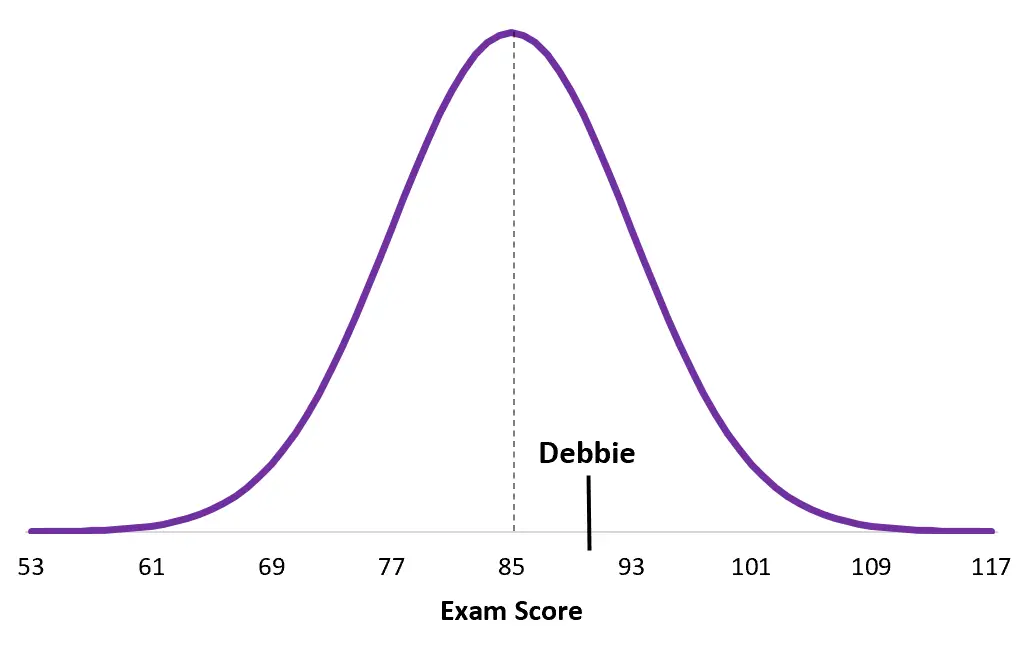
デビーのスコアがデュアンのスコアよりも母集団の平均にどれほど近いかに注目してください。彼女の全体的なスコアは高くなりますが、単に特定の試験の平均スコアが高いため、Z スコアは低くなります。
この例は、Z スコアが異なる分布のデータ値を比較するのに非常に役立つ理由を示しています。Z スコアは分布の平均偏差と標準偏差を考慮するため、異なる分布のデータ値を比較し、どれが正しいかを確認できます。自社のディストリビューションと比較して高い。
追加リソース
Zスコア計算機
Z スコアの比較計算ツール