Sas で qq プロットを作成する方法
「分位数-分位数」の略であるQQ プロットは、データセットが理論的な分布に由来する可能性があるかどうかを評価するために使用されます。
ほとんどの場合、このタイプのプロットは、データ セットが正規分布に従うかどうかを判断するために使用されます。
データが正規分布している場合、QQ プロット上の点は直線の対角線上にあります。
逆に、グラフ上の点が直線の対角線から大きく外れると、データセットが正規分布に従う可能性が低くなります。
SAS で QQ プロットを作成する最も簡単な方法は、 PROC UNIVARIATEステートメントをQQPLOTステートメントとともに使用することです。
proc univariate data =my_data noprint ; qqplot my_variable; run ;
次の例は、この構文を実際に使用する方法を示しています。
注: NOPRINTステートメントを使用して、 PROC UNIVARIATEステートメントによって自動的に生成された他のすべての要約統計とテーブルを削除します。
例 1: SAS で通常データの QQ プロットを作成する
次のコードは、平均 10、標準偏差 2 の正規分布から生成された 1000 個の観測値を含むデータ セットの QQ プロットを作成する方法を示しています。
/*generate 1000 values that follow normal distribution with mean 10 and sd 2 */
data normal_data;
do i = 1 to 1000;
x = 10 + 2* rannor (1);
output ;
end ;
run ;
/*create some plot*/
proc univariate data =normal_data noprint ;
qqplot x;
run ;
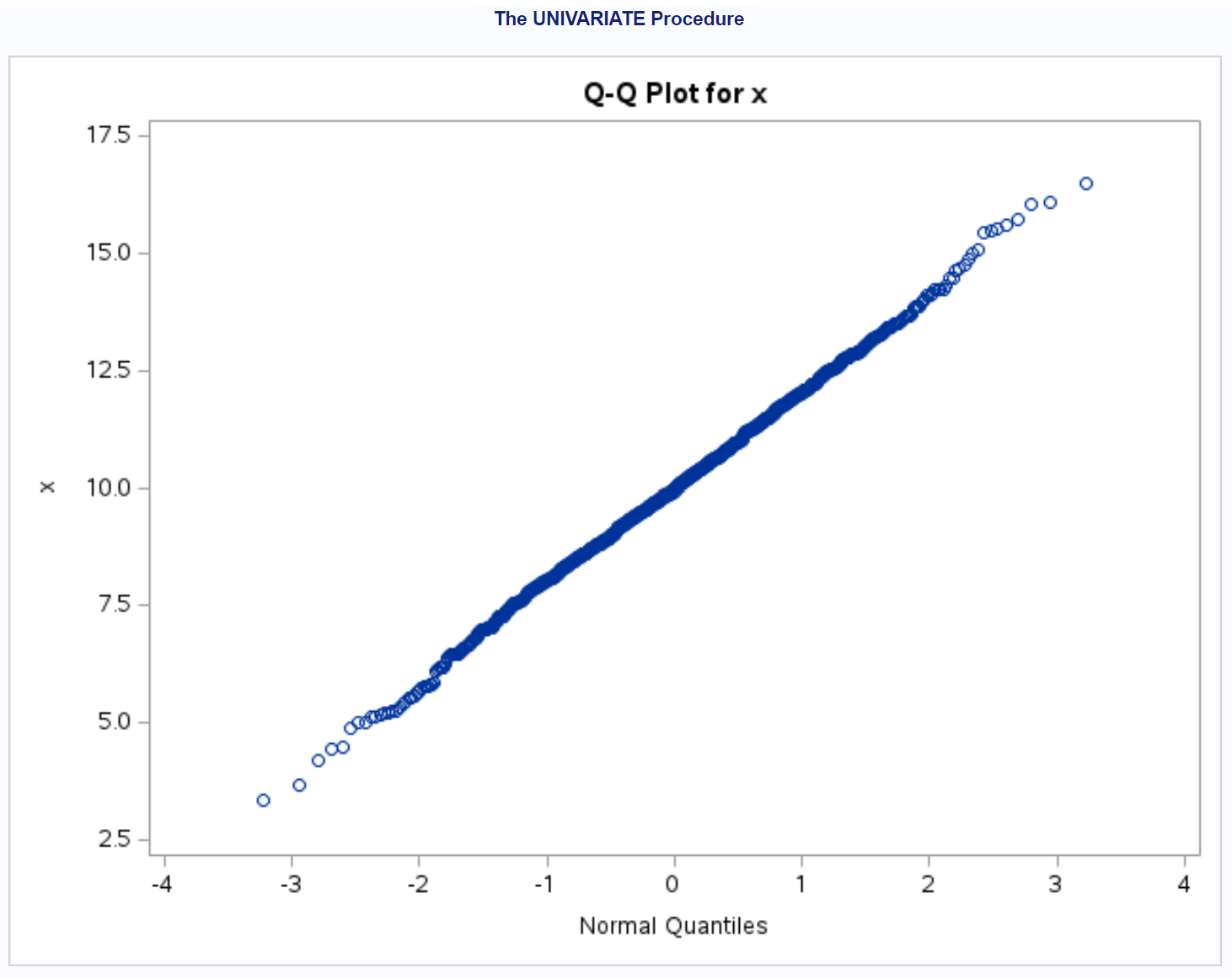
点はほとんど直線の対角線に沿って配置されていますが、各尾部に沿って多少のずれがあることがわかります。
このグラフに基づいて、このデータセットは正規分布していると安全に仮定できます。
例 2: 非正規データの QQ プロット
次のコードは、指数分布から生成された 1000 個の観測値を含むデータセットの QQ プロットを作成する方法を示しています。
/*generate 1000 values that follow an exponential distribution*/
data exp_data;
do i = 1 to 1000;
x = ranexp (1);
output ;
end ;
run ;
/*create some plot*/
proc univariate data =exp_data noprint ;
qqplot x;
run ;
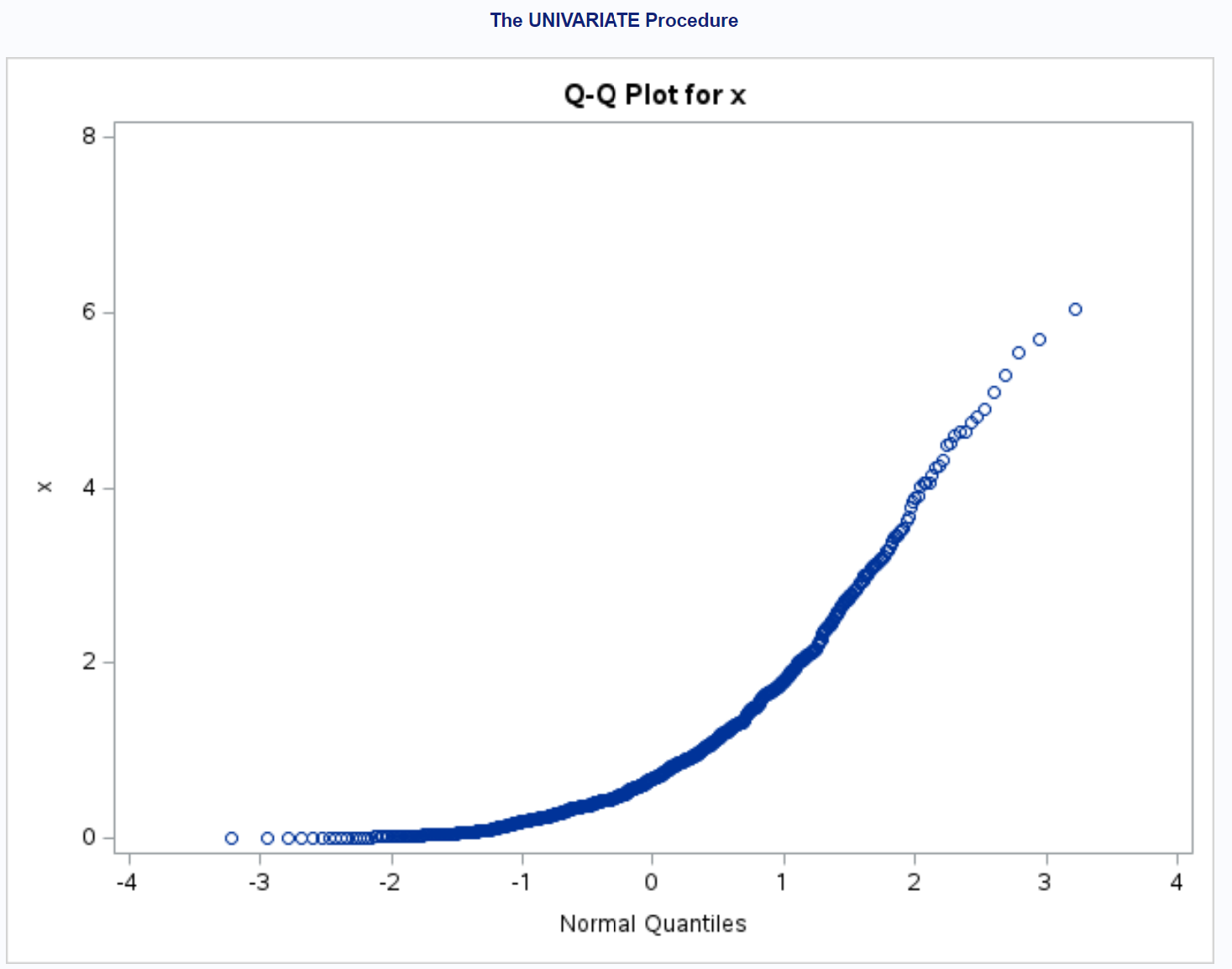
点が直線の対角線から大きくずれていることがわかります。これは、データセットが正規分布していないことを明確に示しています。
データが指数分布に従うように指定したことを考えると、これは当然のことです。
追加リソース
次のチュートリアルでは、SAS で他の一般的なタスクを実行する方法について説明します。
SAS で正規性テストに Proc Univariate を使用する方法
SAS でログ変換を実行する方法
SAS で外れ値を特定する方法