ばらばらなイベントとは何ですか? (定義と例)
独立したイベントとは、同時に発生することができないイベントです。
確率表記で書くと、イベントAとB は、交差部分が 0 の場合、互いに素です。これは次のように記述できます。
- P(A および B) = 0
- P(A∩B) = 0
たとえば、デッキからランダムにカードを選択するとします。イベント A をカードがスペードまたはクラブであるイベントとし、イベント B をカードがハートまたはダイヤであるイベントとする。
イベントのサンプル空間を次のように定義します。
- A = {スペード、クラブ}
- B = {ハート、ダイヤモンド}
2 つのサンプリングされた空間の間に重なりがないことに注意してください。したがって、イベント A と B は同時に発生することができないため、独立したイベントになります。
注:互いに素なイベントは、相互排他的 であるとも言われます。
ばらばらなイベントの例
以下に、関連性のないイベントの例をいくつか示します。
例 1: ドロー
コインを投げるとします。イベント A をコインが表で着地するイベント、イベント B をコインが表で着地するイベントとしましょう。
イベント A とイベント B は、両方を同時に発生させることができないため、切り離されたものになります。コインは表または裏に着地することはできません。
例 2: サイコロを振る
サイコロを振ったとします。イベント A をサイコロの目が奇数の場合のイベント、イベント B をサイコロの目が偶数の場合のイベントとします。
イベント A とイベント B は、両方を同時に発生させることができないため、切り離されたものになります。サイコロの目は偶数にも奇数にもなりません。
例 3: プロボウルの場所
NFL がプロボウルを開催する場所を選択したいとします。彼らはマイアミとサンディエゴに選択肢を絞り込んだ。彼らは 2 人の名前を帽子の中に入れ、ランダムに 1 つを選びます。イベント A がマイアミを選択したイベントで、イベント B がサンディエゴを選択したイベントだと仮定します。
イベント A とイベント B は、両方を同時に発生させることができないため、切り離されたものになります。マイアミとサンディエゴを両方選択することはできません。
切り離されたイベントを表示する
素のイベントを視覚化する便利な方法は、ベン図を作成することです。
2 つのイベントが互いに素である場合、ベン図ではそれらはまったく重なりません。
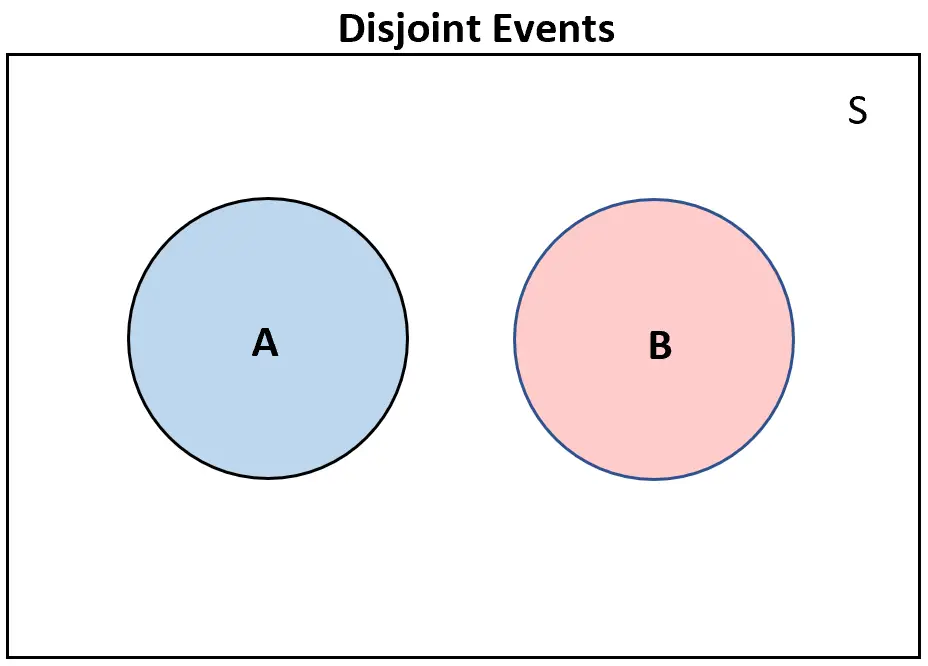
逆に、2 つのイベントが互いに素でない場合、ベン図には少なくともある程度の重複が存在します。
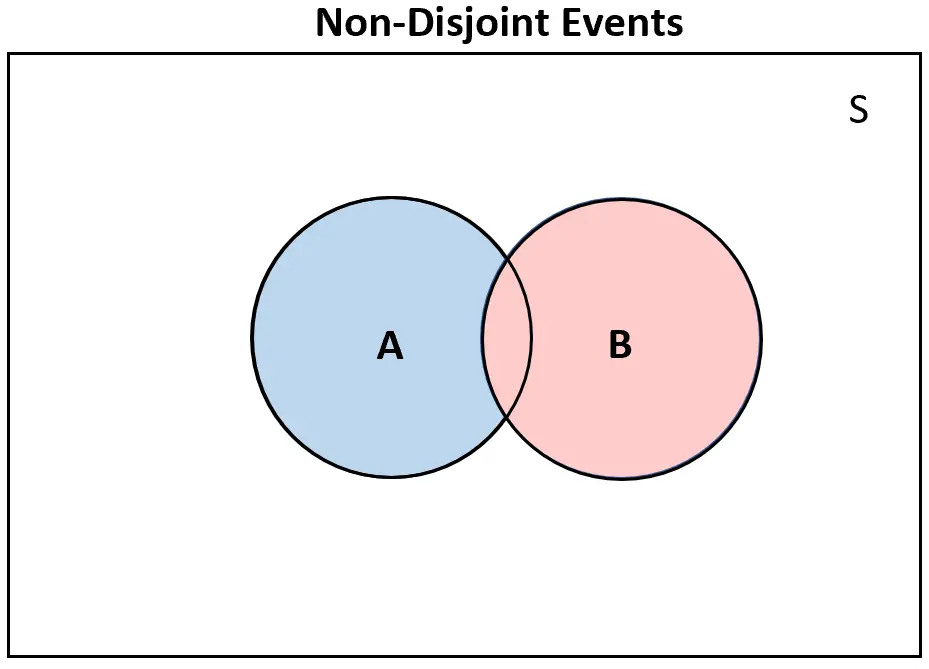
互いに素な出来事が起こる確率
前述したように、2 つのイベントが互いに素である場合、両方が同時に発生する確率はゼロです。
- P(A∩B) = 0
同様に、どちらかのイベントが発生する確率は、個々の確率を加算することで計算できます。
- P(A∪B) = P(A) + P(B)
たとえば、イベント A をサイコロの目が 1 または 2 に出るイベントとし、イベント B をサイコロの目が 5 または 6 の目に出るイベントだとします。
イベントのサンプル空間を次のように定義します。
- A = {1, 2}
- B = {5, 6}
イベント A またはイベント B が発生する確率は次のように計算します。
- P(A∪B) = P(A) + P(B)
- P(A∪B) = 2/6 + 2/6
- P(A∪B) = 4/6 = 2/3
イベント Aまたはイベント B が発生する確率は2/3です。
追加リソース
次のチュートリアルでは、その他の一般的な確率トピックについて説明します。