Ancova (分散分析) の概要

ANCOVAは「共分散分析」の略です。 ANOVA がどのように機能するかを理解するには、まず ANOVA について理解することが役立ちます。

分散分析  (分散分析) は、3 つ以上の独立したグループの平均間に統計的に有意な差があるかどうかを判断するために使用されます。

たとえば、学習テクニックがあるクラスの生徒の試験の得点に影響を与えるかどうかを知りたいとします。私たちはクラスをランダムに 3 つのグループに分けました。各グループは、試験に備えて 1 か月間、異なる学習方法を使用します。月末に、生徒全員が同じ試験を受けます。

勉強方法が試験のスコアに影響を与えるかどうかを調べるには、一元配置分散分析を実行します。これにより、3 つのグループの平均スコア間に統計的に有意な差があるかどうかがわかります。

ANOVAは ANOVA の拡張であり、 1 つ以上の共変量を考慮した後で 3 つ以上の独立したグループ間に統計的に有意な差があるかどうかを判断します。

共変量は、応答変数に応じて変化する連続変数です。

たとえば、学習テクニックが試験の得点に影響を与えるかどうかを知りたいが、その生徒がクラス内ですでに獲得している成績を考慮したいとします。現在の成績を共変量として使用し、ANCOVA を実行して、3 つのグループの平均試験スコア間に統計的に有意な差があるかどうかを判断できます。

これにより、共変量の影響を取り除いた後、学習テクニックが試験の得点に影響を与えるかどうかをテストすることができます。

したがって、3 つの学習方法の間に試験の得点に統計的に有意な差があることが判明した場合、クラス内での生徒の現在の成績を考慮した後でも、この差が存在することを確信できます (c ‘つまり、すでにうまくいっている、またはすでにうまくいっている場合）。授業中ではありません） 。

ANCOVA の仮定

ANCOVA を実行する前に、次の前提条件が満たされていることを確認することが重要です。

• 共変量と因子変数は独立しています– モデルに共変量項を追加することは、共変量と因子変数が独立して作用する場合にのみ意味があるため、共変量と因子変数は互いに独立している必要があります。応答変数 。
• 共変量は連続データです。共変量は連続的でなければなりません (つまり、間隔または比率データ)。
• 分散の均一性– グループ間の分散はほぼ等しい必要があります。
• 独立性– 各グループの観測は独立している必要があります。
• 正規性– データは各グループにほぼ正規分布する必要があります。
• 極端な外れ値がない– どのグループにも、ANCOVA の結果に重大な影響を与える可能性のある極端な外れ値があってはなりません。

ANCOVA: 例

教師は、3 つの異なる学習方法が試験の得点に影響するかどうかを知りたいと考えていますが、生徒がクラス内ですでに獲得している現在の成績を考慮したいと考えています。

次の変数を使用して ANCOVA を実行します。

• 要因変数:技術的検討
• 共変量:現在のスコア
• 応答変数:試験のスコア

次の表は、研究に参加するために募集された 15 人の学生のデータセットを示しています。

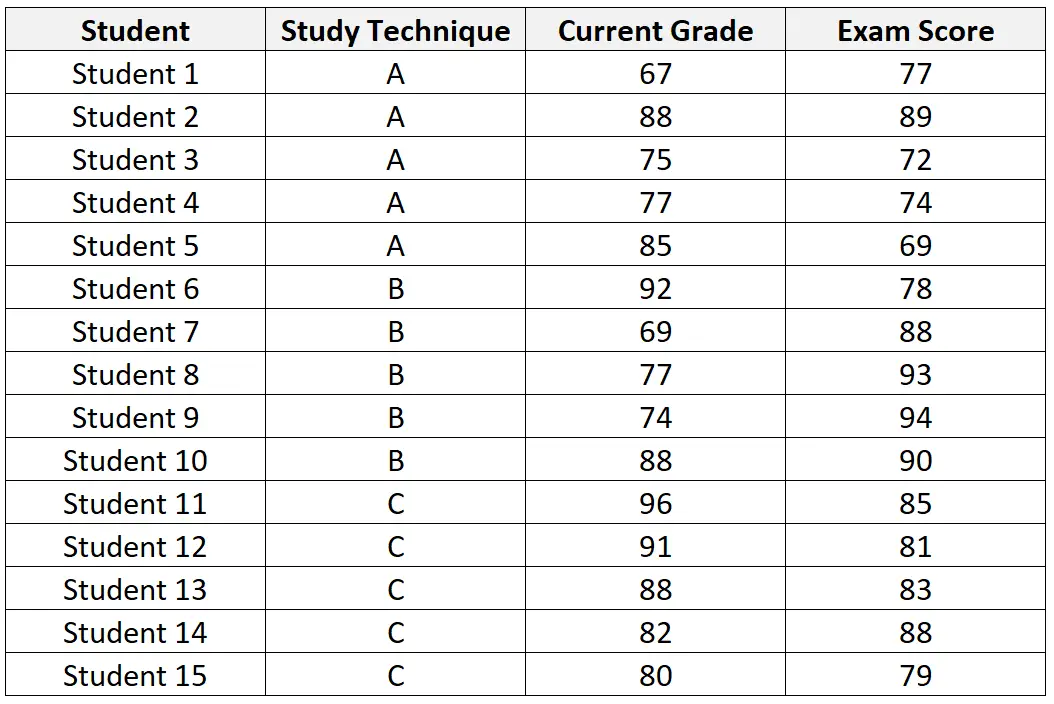
データセットに対して ANCOVA を実行した後、教師は次の結果を取得します。

研究手法の p 値は0.03155です。この値は 0.05 未満であるため、クラス内の生徒の現在の成績を考慮した後でも、各学習テクニックが同じ平均試験成績につながるという帰無仮説を棄却できます。

どの学習手法が異なる試験平均点をもたらすかを正確に判断するには、教師は事後テストを実施する必要があります。

追加リソース

Excel で ANCOVA を実行する方法
R で ANCOVA を実行する方法
Python で ANCOVA を実行する方法
ANOVA、ANCOVA、MANOVA、MANCOVA の違い