Yate 連続性の修正: 定義と例
独立性のカイ二乗検定は、 2 つのカテゴリ変数間に有意な関連があるかどうかを判断するために使用されます。
この検定では、次の帰無仮説と対立仮説を使用します。
- H 0 : (帰無仮説) 2 つの変数は独立しています。
- H 1 : (対立仮説) 2 つの変数は独立していません。 (つまり、それらは関連付けられています)
次の式を使用して、この検定のカイ 2 乗 x 2検定統計量を計算します。
X 2 = Σ(O i -E i ) 2 / E i
金:
- Σ: 「和」を意味する派手な記号
- ○:実測値
- E:期待値
このテストは、分割表内の頻度の離散確率が連続分布であるカイ二乗分布で近似できることを前提としています。
ただし、この仮定は少し間違っている傾向があり、結果として得られるテスト統計は上方に偏る傾向があります。
このバイアスを補正するには、Yate の連続性補正を適用します。これにより、次の補正が式X2に適用されます。
X 2 = Σ(|O i -E i | – 0.5) 2 / E i
通常、この補正は、分割表内の少なくとも 1 つのセルの予想頻度が 5 未満である場合にのみ使用されます。
例:Yateの連続性補正の適用
性別が政党の好みと関連しているかどうかを知りたいとします。 40 人の有権者から単純に無作為にサンプルを抽出し、政党の好みについて尋ねます。次の表は、調査の結果を示しています。

Yate の連続性補正を使用して独立性のカイ 2 乗検定を実行する方法は次のとおりです。
観測値:

期待値:
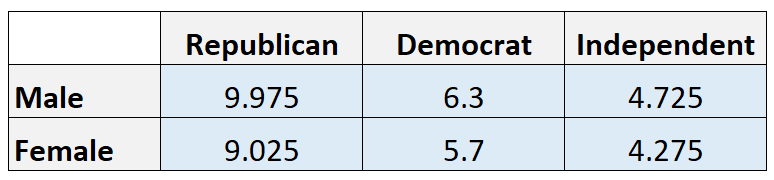
注:各セルの期待値は、行の合計と列の合計を乗算し、総計で割ることによって計算されます。たとえば、共和党男性の予想数は (21*19)/40 = 9.975 です。
カイ二乗検定統計量:
- (|8-9.975| – 0.5) 2 / 9.975 = 0.218
- (|9-6.3| – 0.5) 2 / 6.3 = 0.768
- (|4-4.725| – 0.5) 2 / 4.725 = 0.011
- (|11-9.025| – 0.5) 2 / 9.025 = 0.241
- (|3-5.7| – 0.5) 2 / 5.7 = 0.849
- (|5-4.275| – 0.5) 2 / 4.275 = 0.012
それで、
P 値:カイ二乗から P 値への計算ツールによると、2 自由度のカイ二乗検定統計量に対応する p 値は0.3501です。
この p 値は 0.05 未満ではないため、帰無仮説を棄却できません。これは、性別と政党の好みの間に関連性があると言える十分な証拠がないことを意味します。