Ti-84 電卓で invnorm を使用する方法 (例付き)
TI-84 計算機でinvNorm()関数を使用すると、正規分布に関連付けられた z 臨界値を見つけることができます。
この関数は次の構文を使用します。
invNorm(確率, μ, σ)
金:
- 確率:有意性のレベル
- μ:母集団平均
- σ:母集団標準偏差
TI-84 電卓でこの機能にアクセスするには、 2nd を押してからVARSを押します。これにより、 DISTR画面が表示され、そこでinvNorm()を使用できます。

次の例は、この関数を実際に使用する方法を示しています。
例 1: 片側検定の重要な Z 値
研究者が α = 0.05 を使用して左手の仮説検定を実行するとします。このアルファ レベルに対応する Z 臨界値は何ですか?
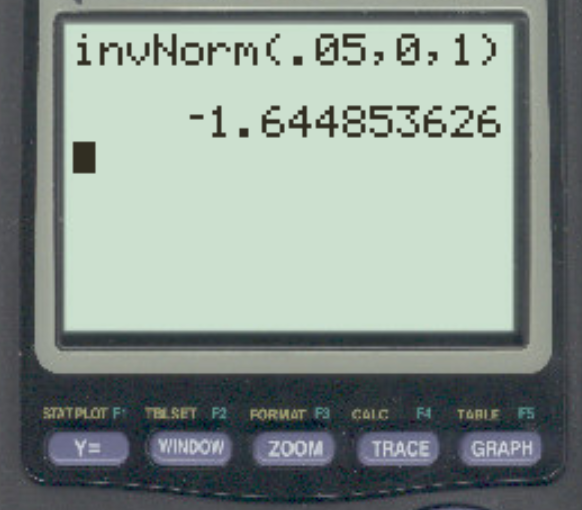
答えは z = -1.64485です。
研究者が α = 0.05 を使用してストレートな仮説検定を実行するとします。このアルファ レベルに対応する Z 臨界値は何ですか?
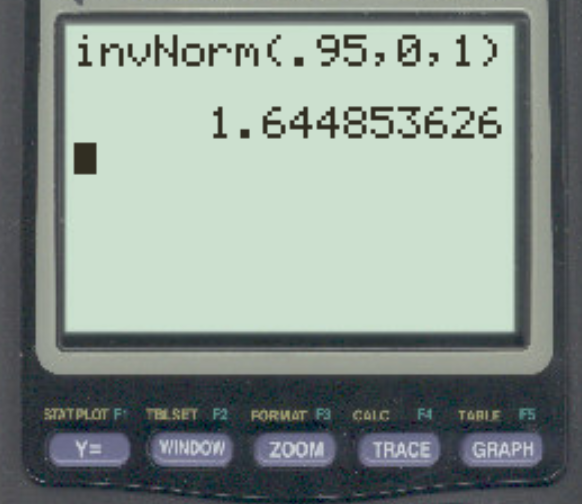
答えは z = 1.64485です。
例 2: 両側テストの臨界 Z 値
研究者が α = 0.05 を使用して両側仮説検定を実行するとします。このアルファ レベルに対応する Z 臨界値は何ですか?
この臨界値を見つけるには、式 1 – α/2 を使用できます。この場合、確率として 1 – 0.05/2 = 0.975 を使用します。
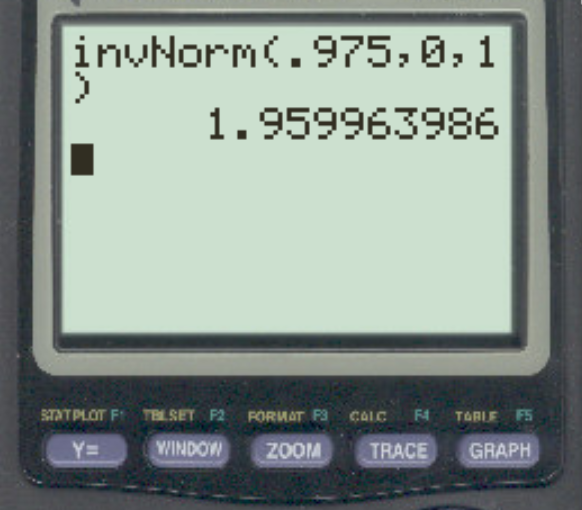
答えは z = 1.96です。
例 3: カットオフ スコアの臨界 Z 値
特定の試験のスコアが平均 70、標準偏差 8 で正規分布していると仮定します。上位 10% と残りを分けるスコアは何でしょうか?
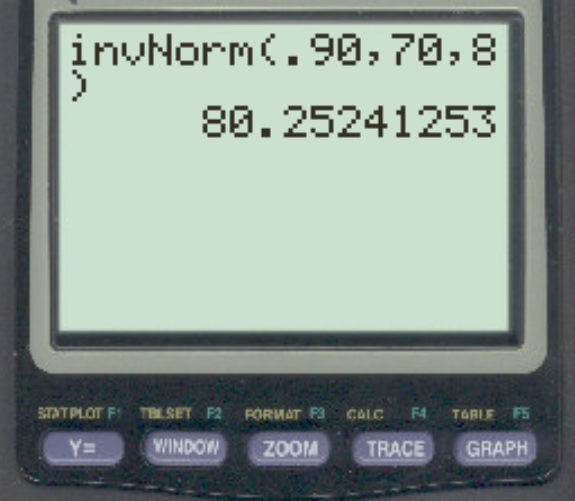
答えは80.25です。
特定の都市の男性の身長が平均 68 インチ、標準偏差 4 インチで正規分布しているとします。下位 25% と残りの部分はどれくらい離れていますか?
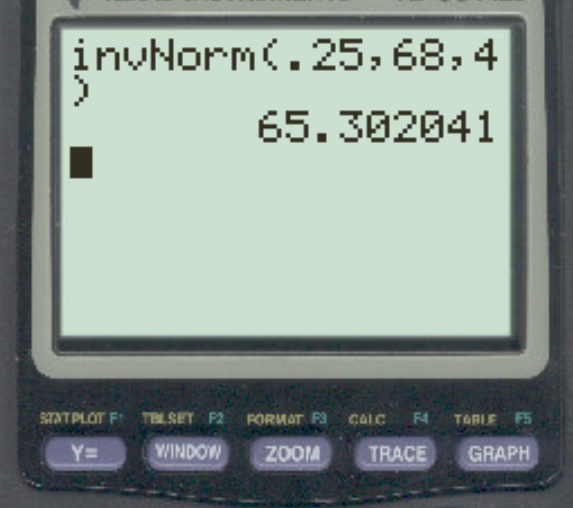
答えは65.3インチです。
追加リソース
TI-84 電卓で二項確率を計算する方法
TI-84 計算機でポアソン確率を計算する方法
TI-84 電卓で幾何学的確率を計算する方法