Wilcoxon 符号付き順位テストの実行方法
ウィルコクソンの符号付き順位検定は、対応のある t 検定のノンパラメトリック バージョンです。 2 つの母集団平均値の間に有意差があるかどうかを検定するために使用されます。
Wilcoxon 符号付き順位テストをいつ使用するか
ペアのある t 検定を使用したいが、ペア間の差の分布が著しく非正規分布である場合は、ウィルコクソンの符号付き順位検定を使用します。
差が正規分布していないかどうかを判断する最も簡単な方法は、差のヒストグラムを作成し、それらがある程度正規の「ベル」型の分布に従っているかどうかを確認することです。
対応のある t 検定は正規性からの偏差に対して非常に堅牢であるため、正規分布からの偏差はウィルコクソンの符号付き順位検定の使用を正当化するのに十分な大きさでなければならないことに注意してください。
Wilcoxon Signed Rank テストの受験方法
次の例は、Wilcoxon 符号付きランク テストを実行する方法を示しています。
バスケットボールのコーチは、特定のトレーニング プログラムによって選手のフリースローの数が増加するかどうかを知りたいと考えています。これをテストするために、彼は15人の選手にトレーニングプログラムの前後にフリースローをそれぞれ20本ずつ行うよう依頼した。
各プレーヤーは自分自身と「ペア」になることができるため、コーチはペアのある t 検定を使用して、トレーニング プログラムの前後で行われたフリースローの平均数に有意な差があるかどうかを判断することを計画しました。トレーニング。
ただし、差の分布は非正規であることが判明したため、コーチは代わりにウィルコクソンの符号付きランク テストを使用しました。
次の表は、トレーニング プログラムの前後で、15 人の各プレーヤーが行ったフリー スローの数 (20 回の試行のうち) を示しています。
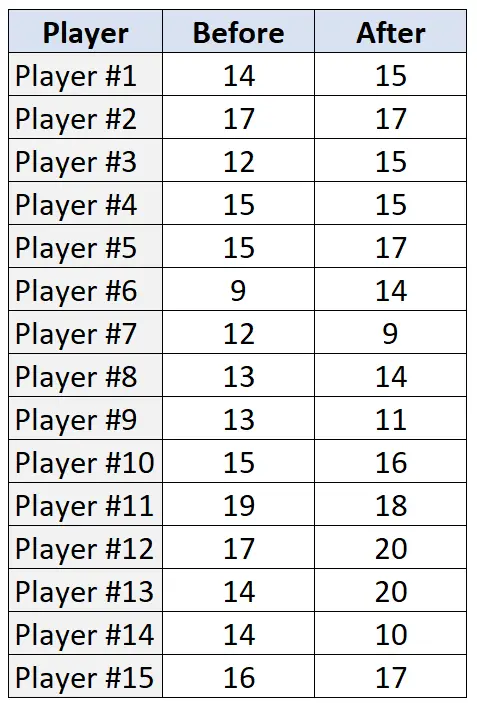
ステップ 1: 帰無仮説と対立仮説を述べます。
H 0 : 2 つのグループ間の差の中央値はゼロです。
H A : 中央値の差がマイナスです。 (例: トレーニング プログラムに参加する前に選手がフリースローの回数を減らすなど)
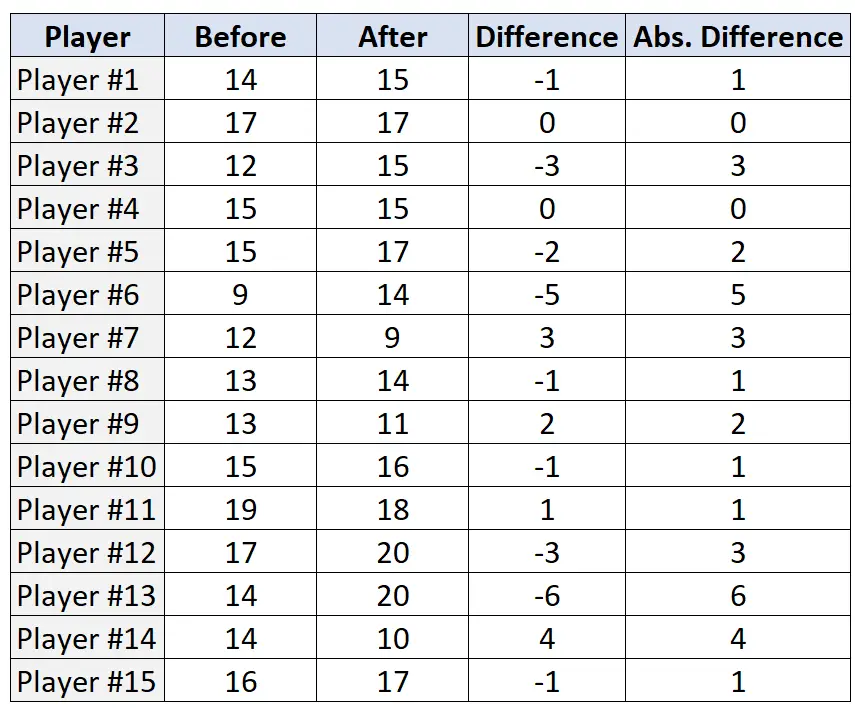
ステップ 2: 各ペアの差と絶対差を見つけます。
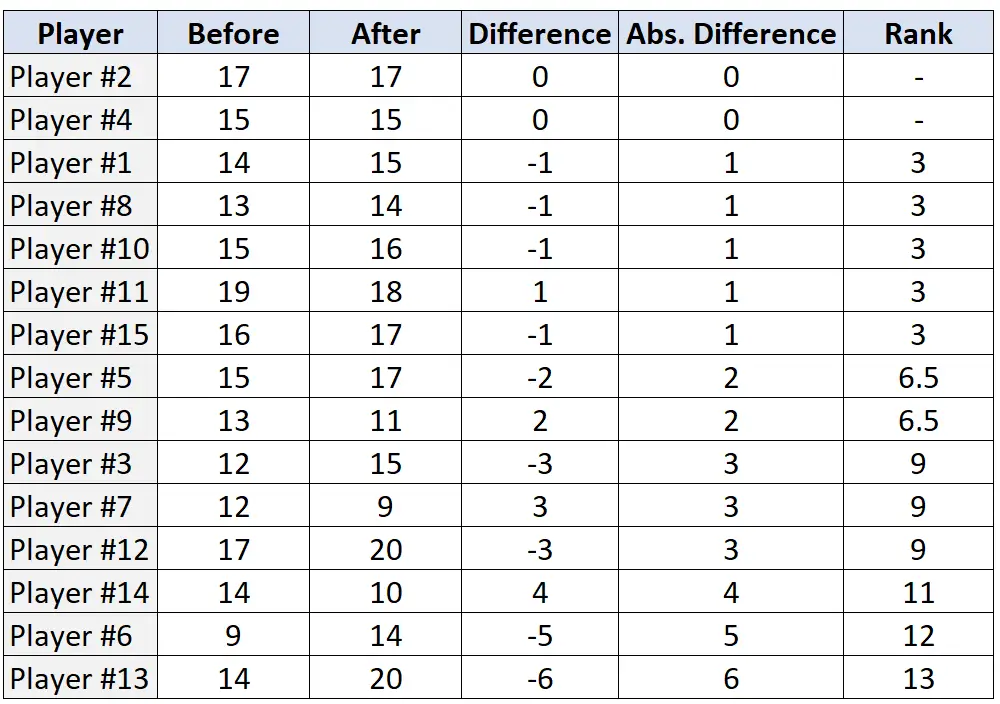
ステップ 3: 絶対差に基づいてペアをランク付けし、絶対差の最小値から最大値までのランクを割り当てます。絶対差が「0」であるペアを無視し、同点の場合は平均順位を割り当てます。
ステップ 4: 正のランクと負のランクの合計を求めます。
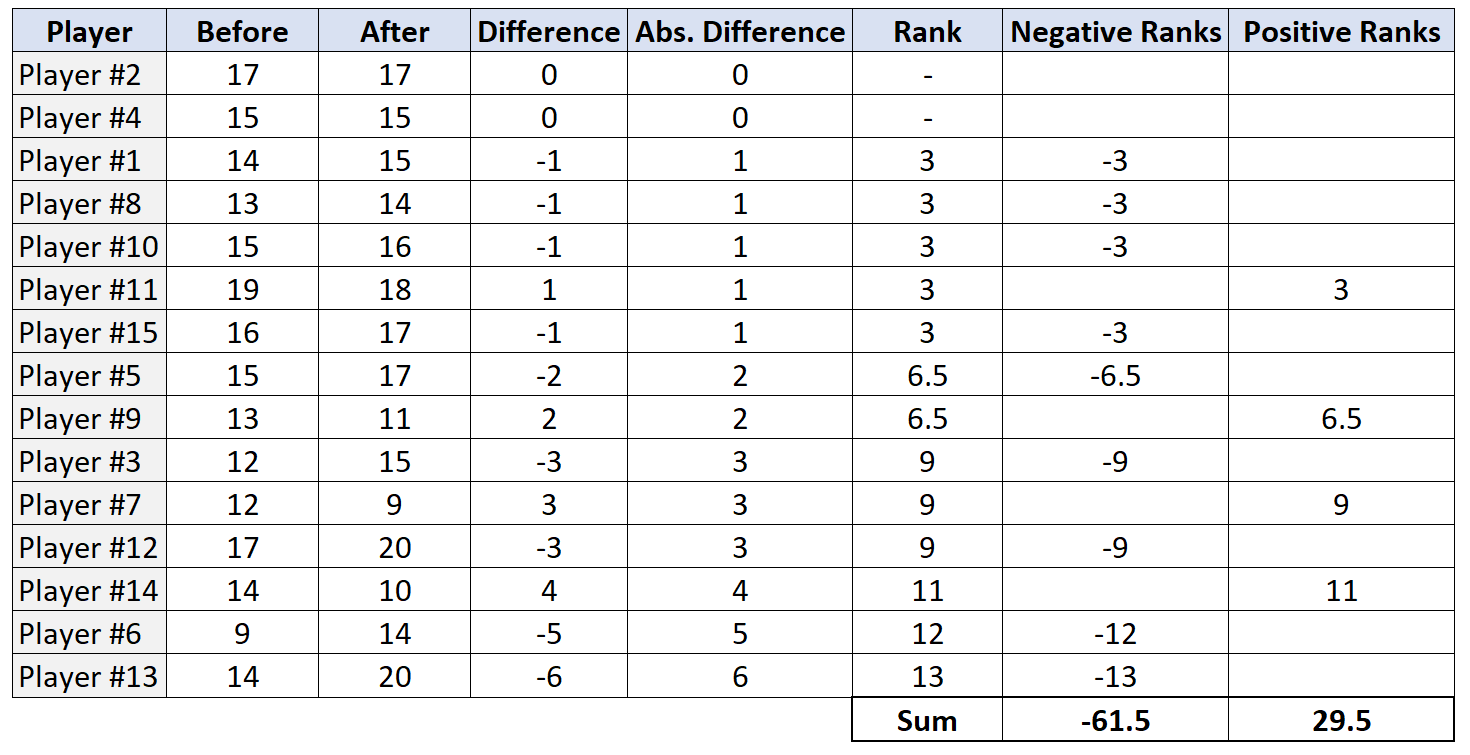
ステップ 5: 帰無仮説を拒否するか、拒否しません。
検定統計量 W は、肯定的なランクと否定的なランクの絶対値の最小値です。この場合、最小値は 29.5 です。したがって、検定統計量は W = 29.5です。
帰無仮説を棄却すべきかどうかを判断するには、 nと選択したアルファ レベルに対応するWilcoxon 符号付き順位検定臨界値テーブルで見つかった臨界値を参照できます。
検定統計量 W が表の臨界値以下の場合、帰無仮説を棄却できます。そうしないと、帰無仮説を棄却できなくなります。
アルファ レベル 0.05 および n = 13 (観測された差が 0 だったためにランクを計算しなかった 2 つのペアを差し引いた合計ペア数) に対応する臨界値は17です。
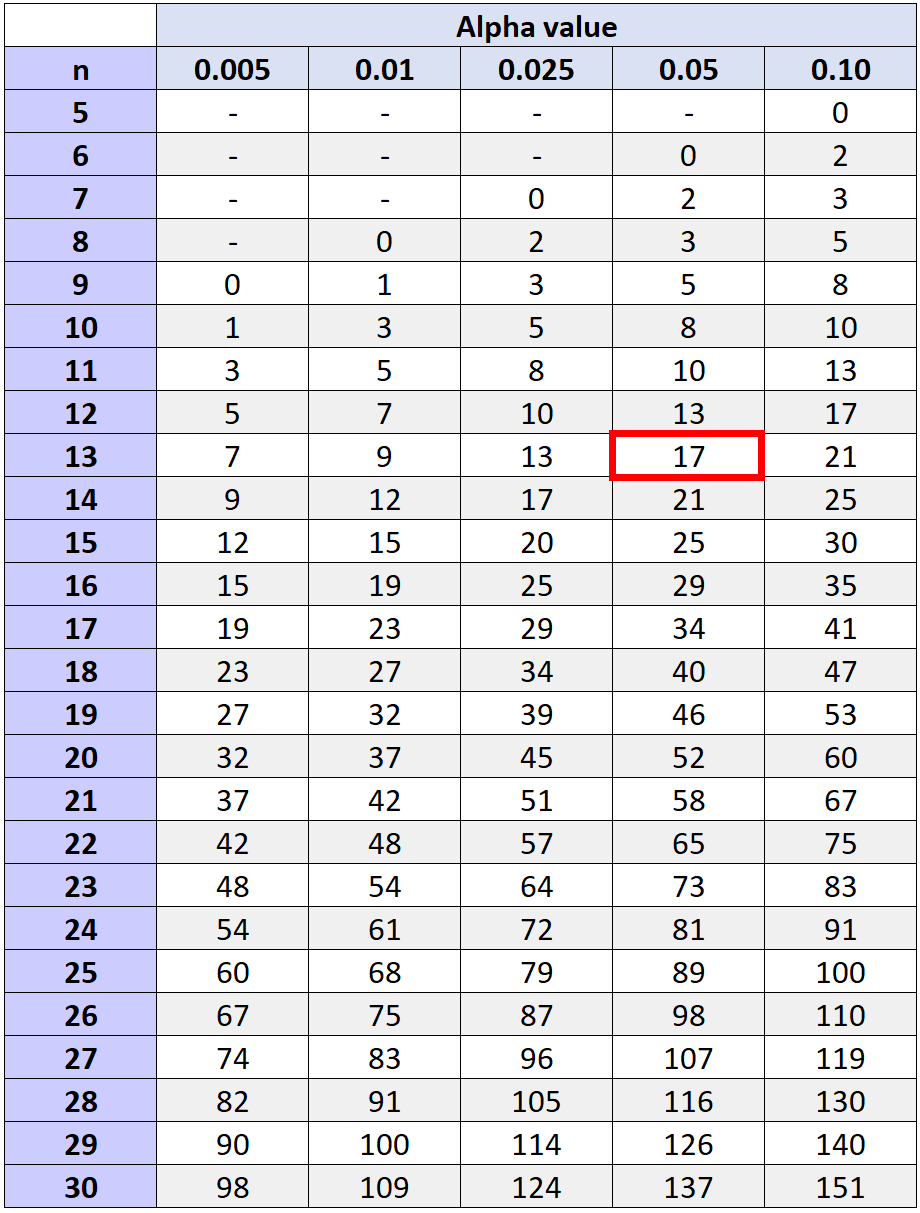
検定統計量 (W = 29.5) が 17 以下ではないため、帰無仮説を棄却できません。このトレーニングプログラムが選手のフリースロー数の大幅な増加につながったと言える十分な証拠はありません。
注:手作業ではなく電卓を使用してテストを実行する場合は、 Wilcoxon Signed Rank Test Calculator を使用してください。