Sas で white のテストを実行する方法

ホワイトの検定は、回帰モデルに不均一分散性が存在するかどうかを判断するために使用されます。

不均一分散性とは、回帰モデル内の応答変数のさまざまなレベルでの残差の不均一な分散を指します。これは、残差が応答変数の各レベルで均等に分散するという線形回帰の重要な前提の1 つに違反します。

このチュートリアルでは、SAS でホワイト テストを実行して、特定の回帰モデルにおいて不均一分散性が問題であるかどうかを判断する方法について説明します。

例: SAS のホワイト テスト

学生の最終試験の成績を予測するために、学習に費やした時間数と受験した模擬試験の数を使用する重線形回帰モデルを当てはめるとします。

試験のスコア = β ₀ + β ₁ (時間) + β ₂ (予備試験)

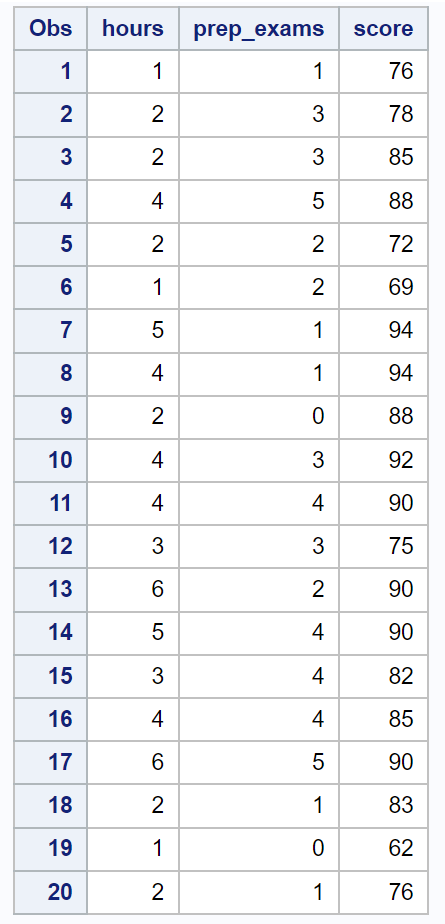
まず、次のコードを使用して、20 人の生徒の情報を含むデータセットを作成します。

 /*create dataset*/
data exam_data;
    input hours prep_exams score;
    datalines ;
1 1 76
2 3 78
2 3 85
4 5 88
2 2 72
1 2 69
5 1 94
4 1 94
2 0 88
4 3 92
4 4 90
3 3 75
6 2 90
5 4 90
3 4 82
4 4 85
6 5 90
2 1 83
1 0 62
2 1 76
;
run ;

/*view dataset*/
proc print data =exam_data; 

次に、 proc regを使用してこの重線形回帰モデルを近似するとともに、 specオプションを使用して不均一分散性の White のテストを実行します。

 /*fit regression model and perform White's test*/
proc reg data =exam_data;
    model score = hours prep_exams / spec ;
run ;
quit ; 

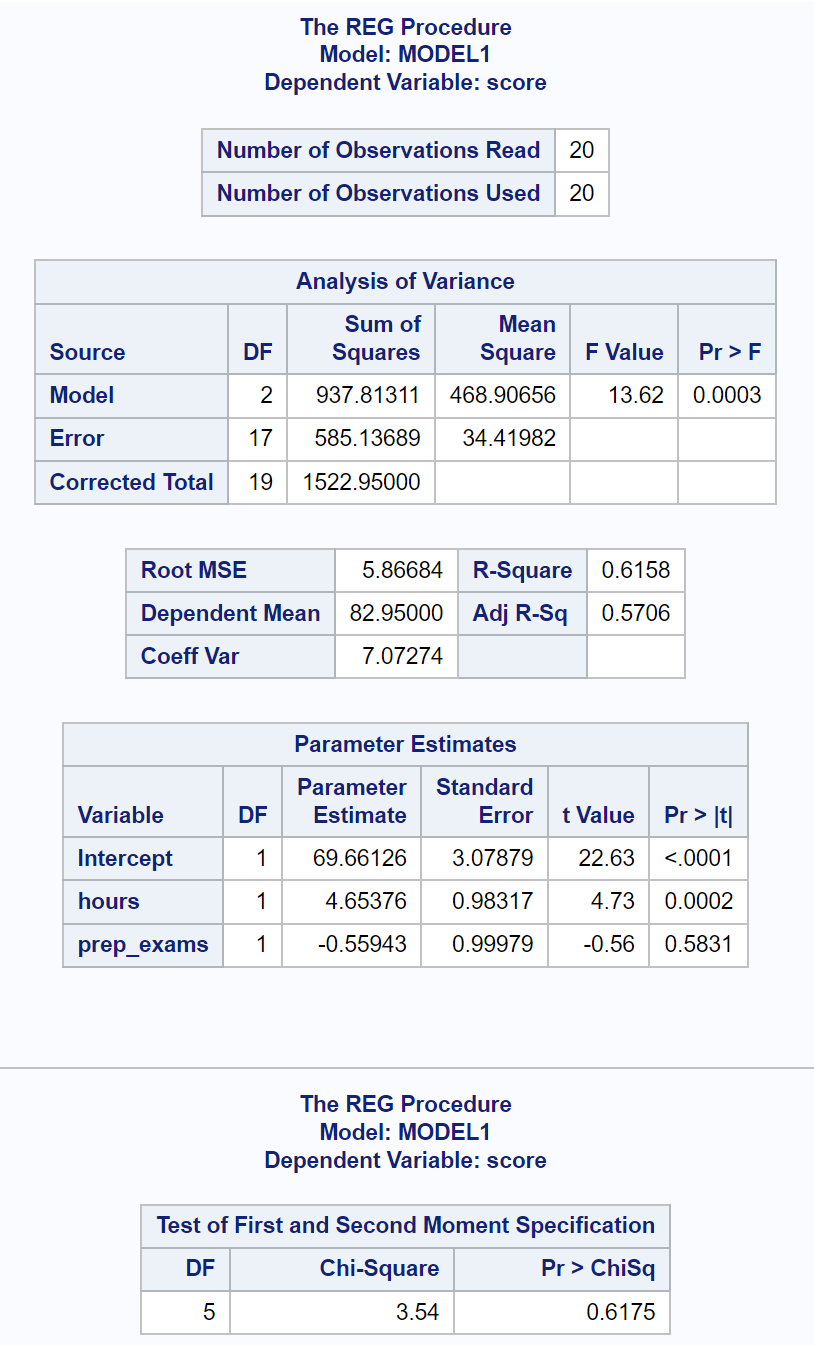
最後の結果表は、White のテストの結果を示しています。

この表から、カイ二乗検定統計量が3.54で、対応する p 値が0.6175であることがわかります。

ホワイト検定では、次の帰無仮説と対立仮説を使用します。

• Null (H ₀ ) : 不均一分散性は存在しません。
• 代替 ( _HA ):不均一分散性が存在します。

p 値は 0.05 未満ではないため、帰無仮説を棄却できません。

これは、回帰モデルに不均一分散性が存在すると主張する十分な証拠がないことを意味します。

したがって、回帰要約テーブルの係数推定値の標準誤差を安全に解釈することができます。

次はどうする

ホワイトの検定の帰無仮説を棄却できなかった場合、不均一分散性は存在しないため、元の回帰の結果の解釈に進むことができます。

ただし、帰無仮説を棄却した場合は、データに不均一分散性が存在することを意味します。この場合、回帰出力テーブルに表示される標準誤差は信頼できない可能性があります。

この問題を解決するには、次のような一般的な方法がいくつかあります。

1. 応答変数を変換します。応答変数に対して変換を実行してみることができます。

たとえば、元の応答変数の代わりにログ応答変数を使用できます。

一般に、応答変数の対数を取ることは、不均一分散性を解消する効果的な方法です。

もう 1 つの一般的な変換は、応答変数の平方根を使用することです。

2. 重み付け回帰を使用します。このタイプの回帰では、近似値の分散に基づいて各データ ポイントに重みが割り当てられます。

これにより、分散が大きいデータ ポイントに小さな重みが与えられ、残差二乗が減少します。

適切な重みを使用すると、不均一分散性の問題を解決できます。