Sas でフィッシャーの正確確率検定を実行する方法
フィッシャーの直接確率検定は、 2 つのカテゴリ変数間に有意な関連があるかどうかを判断するために使用されます。
これは通常、2 × 2 テーブル内の 1 つ以上のセル数が 5 未満である場合に、 独立性のカイ二乗検定の代替として使用されます。
フィッシャーの正確検定では、次の帰無仮説と対立仮説が使用されます。
- H 0 : (帰無仮説) 2 つの変数は独立しています。
- H 1 : (対立仮説) 2 つの変数は独立していません。
検定のp 値が特定の有意水準未満の場合、検定の帰無仮説は棄却され、2 つの変数は独立していないと結論付けることができます。つまり、それらには有意な関連性があると言えます。
次の例は、SAS でフィッシャーの正確確率検定を実行する方法を示しています。
例: SAS のフィッシャーの正確確率検定
特定の大学での政党への選好に性別が関連しているかどうかを知りたいとします。
これを調査するために、キャンパス内で 25 人の学生をランダムに選び、希望する政党について尋ねます。結果を以下の表に示します。
| 民主党 | 共和党 | |
|---|---|---|
| 女性 | 8 | 4 |
| 男 | 4 | 9 |
性別と政党の好みの間に統計的に有意な関連があるかどうかを判断するには、次の手順を使用して SAS でフィッシャーの直接確率検定を実行できます。
ステップ 1: データを作成する
まず、 my_dataというデータセットを作成しましょう。
/*create data to hold survey results*/ data my_data; input Party$Gender$; datalines ; Rep Female Rep Female Rep Female Rep Female Rep Male Rep Male Rep Male Rep Male Rep Male Rep Male Rep Male Rep Male Rep Male Dem Female Dem Female Dem Female Dem Female Dem Female Dem Female Dem Female Dem Female Dem Male Dem Male Dem Male Dem Male ; run ;
ステップ 2: フィッシャーの正確確率検定を実行する
次に、次のコードを使用してフィッシャーの正確検定を実行できます。
/*perform Fisher's Exact test*/ proc freq ; Party*Gender / fisher tables ; run ;
テスト結果を以下に示します。
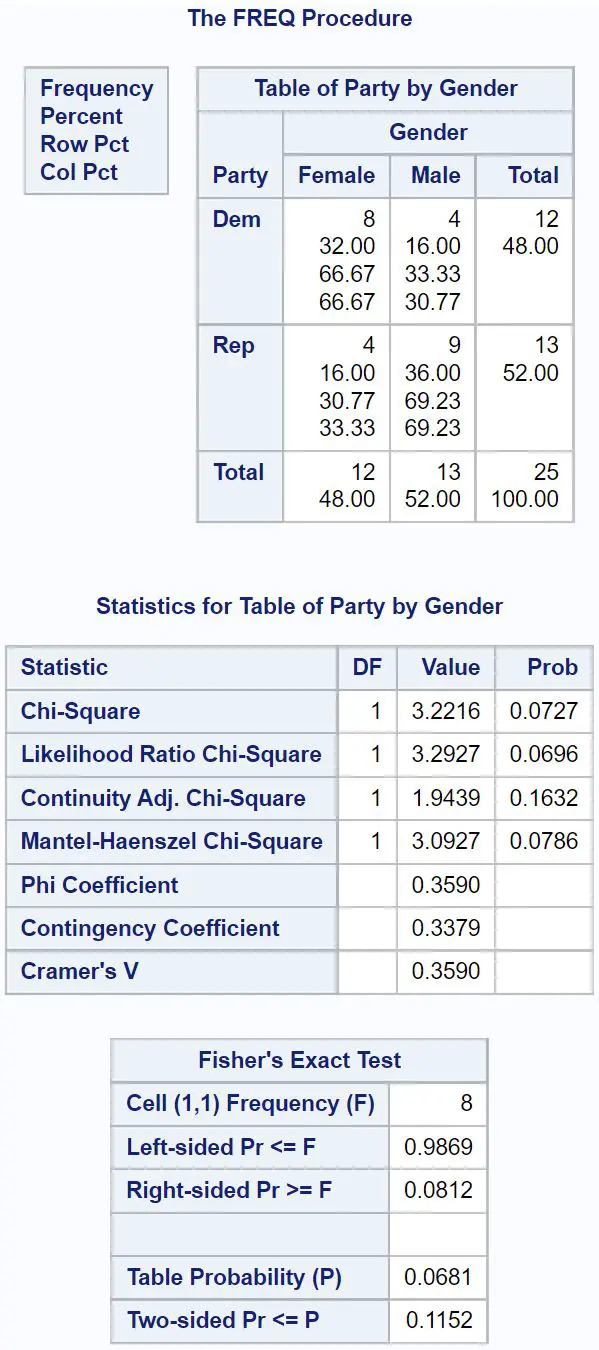
フィッシャーの正確検定の帰無仮説は、2 つの変数が独立であるということです。この例では、性別と政党の好みは独立しているという帰無仮説があり、これは両側検定です。
そこで、最終結果テーブルの両側 p 値を調べます。これは0.1152であることがわかります。
この p 値は 0.05 未満ではないため、帰無仮説は棄却されません。
これは、性別と政党の好みの間に重大な関連があると言える十分な証拠がないことを意味します。
追加リソース
次のチュートリアルでは、フィッシャーの正確確率検定に関する追加情報を提供します。