Excel で anova 結果をグラフ化する方法

によるベンジャミン・アンダーソン博士 7月 3, 2023 ガイド 0コメント

一元配置分散分析は、 3 つ以上の独立したグループの平均間に統計的に有意な差があるかどうかを判断するために使用されます。

一元配置分散分析の結果を解釈する場合、グループ平均間の差異を視覚化するグラフを作成すると役立つ場合があります。

次の例は、一元配置分散分析を実行し、結果を Excel でグラフ化する方法を示しています。

例: Excel で ANOVA 結果をグラフ化する方法

教授がクラスの 30 人の生徒に、試験の準備のために 3 つの勉強方法のうちの 1 つを使用するようにランダムに依頼したとします。

次のスクリーンショットは、生徒が使用した方法に基づく生徒のスコアを示しています。

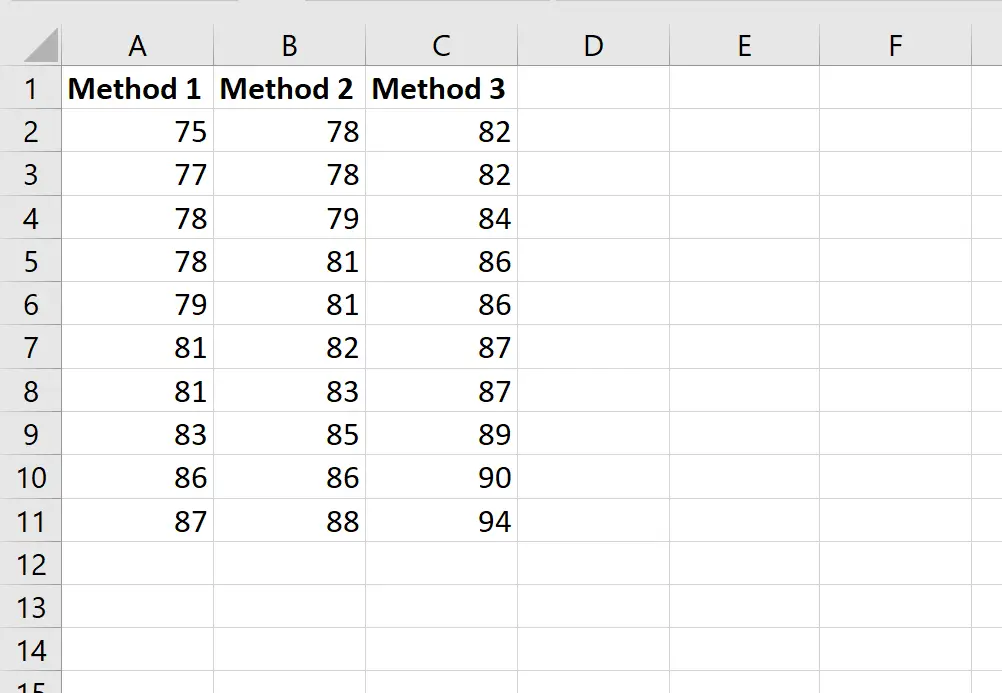
教授が一元配置分散分析を実行して、平均スコアが 3 つのグループ間で同じかどうかを判断したいと考えているとします。

Excel で一元配置分散分析を実行するには、上部のリボンに沿って[データ]タブをクリックし、 [分析]グループの[データ分析]をクリックします。

[データ分析]オプションが表示されない場合は、まず無料の分析ツールソフトウェアをロードする必要があります。

表示される新しいパネルで、 [Anova: Single Factor]をクリックし、 [OK]をクリックします。

表示される新しいウィンドウで、次の情報を入力します。

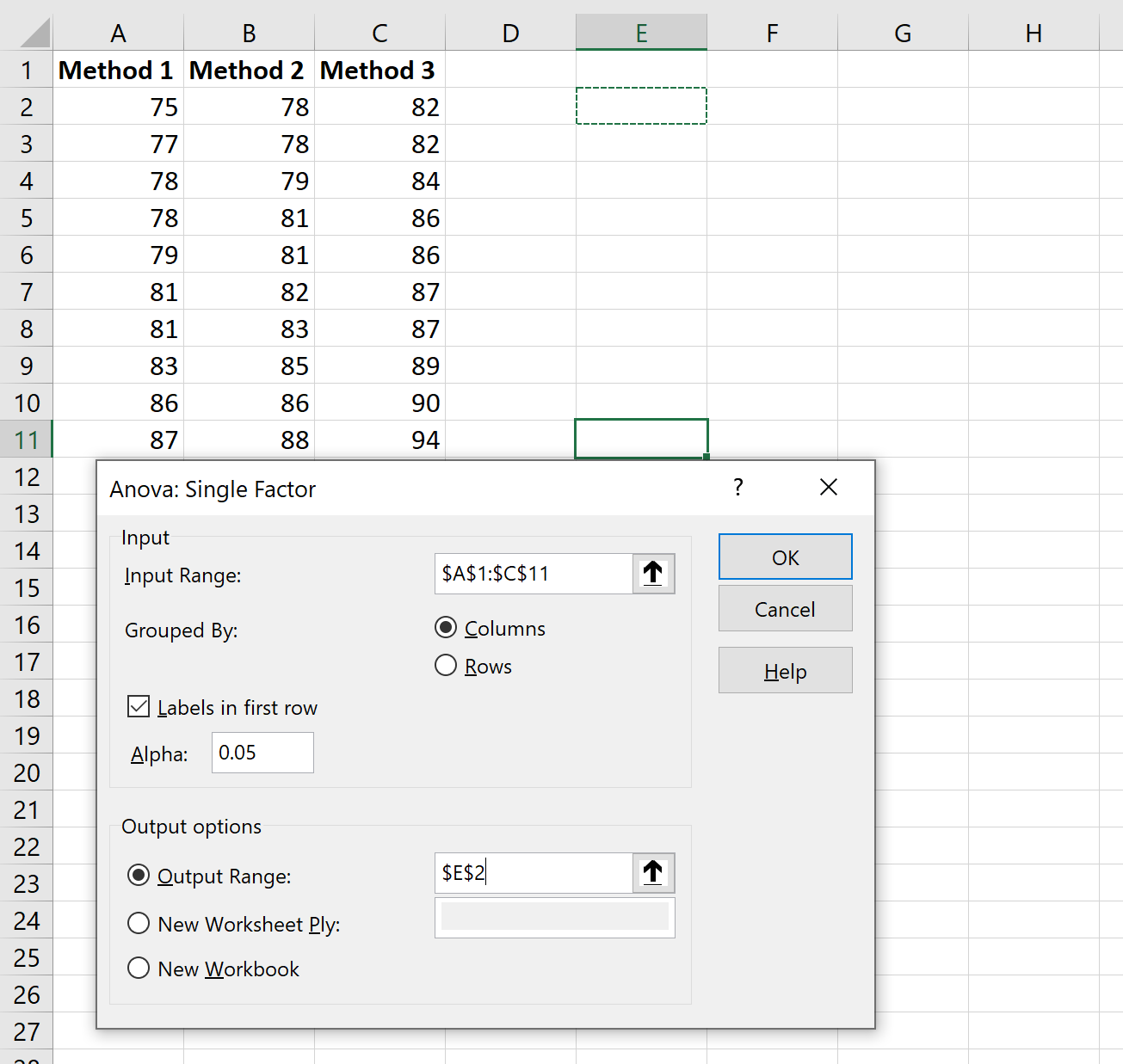
[OK]をクリックすると、一元配置分散分析の結果が表示されます。

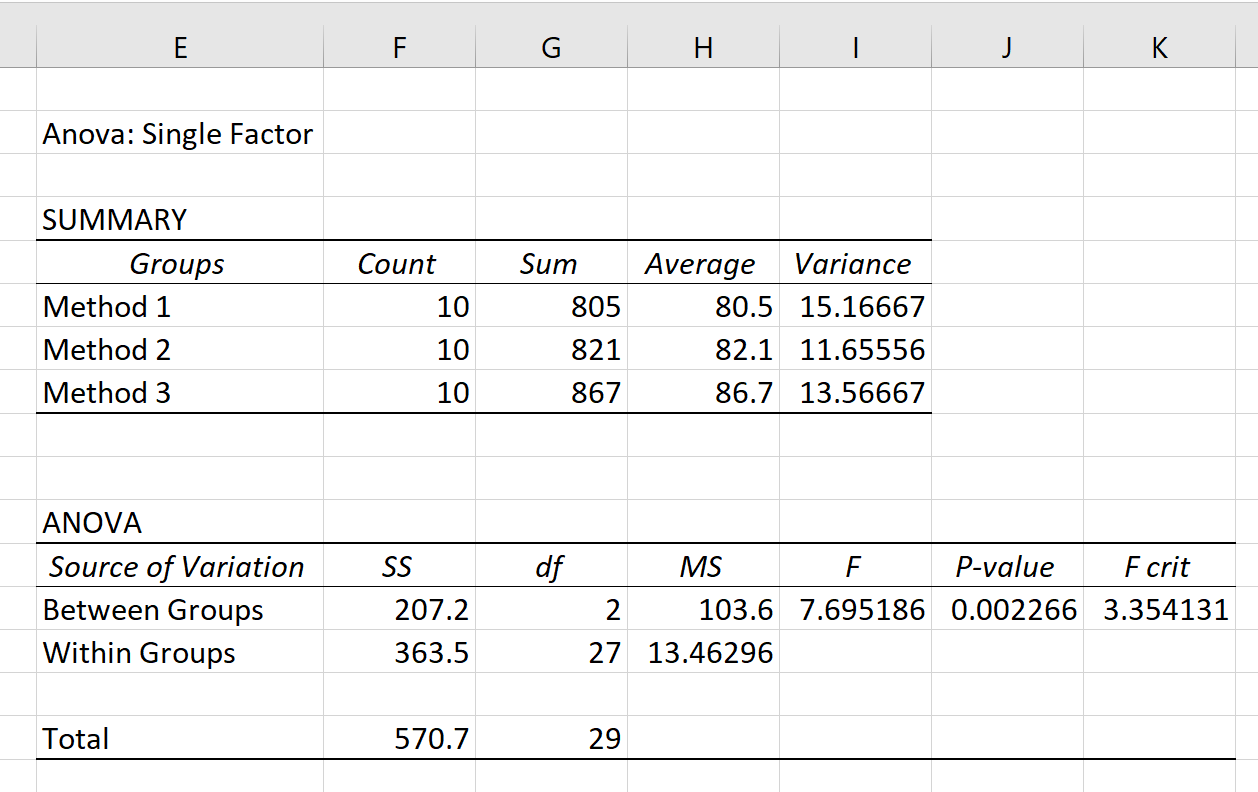
出力の最大値はp 値で、 0.002266であることがわかります。

一元配置分散分析では次の帰無仮説と対立仮説が使用されることを思い出してください。

p 値は α = 0.05 より小さいため、帰無仮説は棄却され、すべてのグループ平均は等しくないと結論付けられます。

これは、3 つの勉強方法すべてが同じ試験平均点につながるわけではないことを意味します。

これらの ANOVA 結果を視覚化するために、各研究方法の試験結果の分布を示すグループ化箱ひげ図を作成できます。

これを行うには、セル範囲A2:C11を強調表示し、上部のリボンに沿って[挿入]タブをクリックし、 [グラフ]グループの[箱とひげ]アイコンをクリックします。

次の表が表示されます。

このグラフを読みやすくするために、Y 軸の範囲を自由に変更し、凡例を追加してください。

それぞれの箱ひげ図には、各研究方法の試験結果の分布が表示されます。

各箱ひげ図の中央の線は各学習方法の試験スコアの中央値を表し、小さな「x」は試験スコアの平均を表します。

ANOVA 表の結果を見なくても、勉強法 3 の試験の平均点が他の 2 つの勉強法よりも大幅に高いことがわかります。

また、ANOVA 表の p 値が統計的に有意である理由もわかります。3 つの研究方法の平均値は明らかに同じではありません。

これら 3 つの箱ひげ図を作成することで、一元配置分散分析の結果をより深く理解できるようになります。

次のチュートリアルでは、Excel で他の一般的な操作を実行する方法について説明します。

私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る