Excel で平均の標準誤差を計算する方法

平均の標準誤差は、データセット内の値の分布を測定する方法です。次のように計算されます。

標準誤差 = s / √n

金：

• s : サンプル標準偏差
• n : サンプルサイズ

次の式を使用して、Excel で任意のデータセットの平均の標準誤差を計算できます。

= STDEV (値の範囲) / SQRT ( COUNT (値の範囲))

次の例は、この式の使用方法を示しています。

例: Excel の標準エラー

次のデータセットがあるとします。

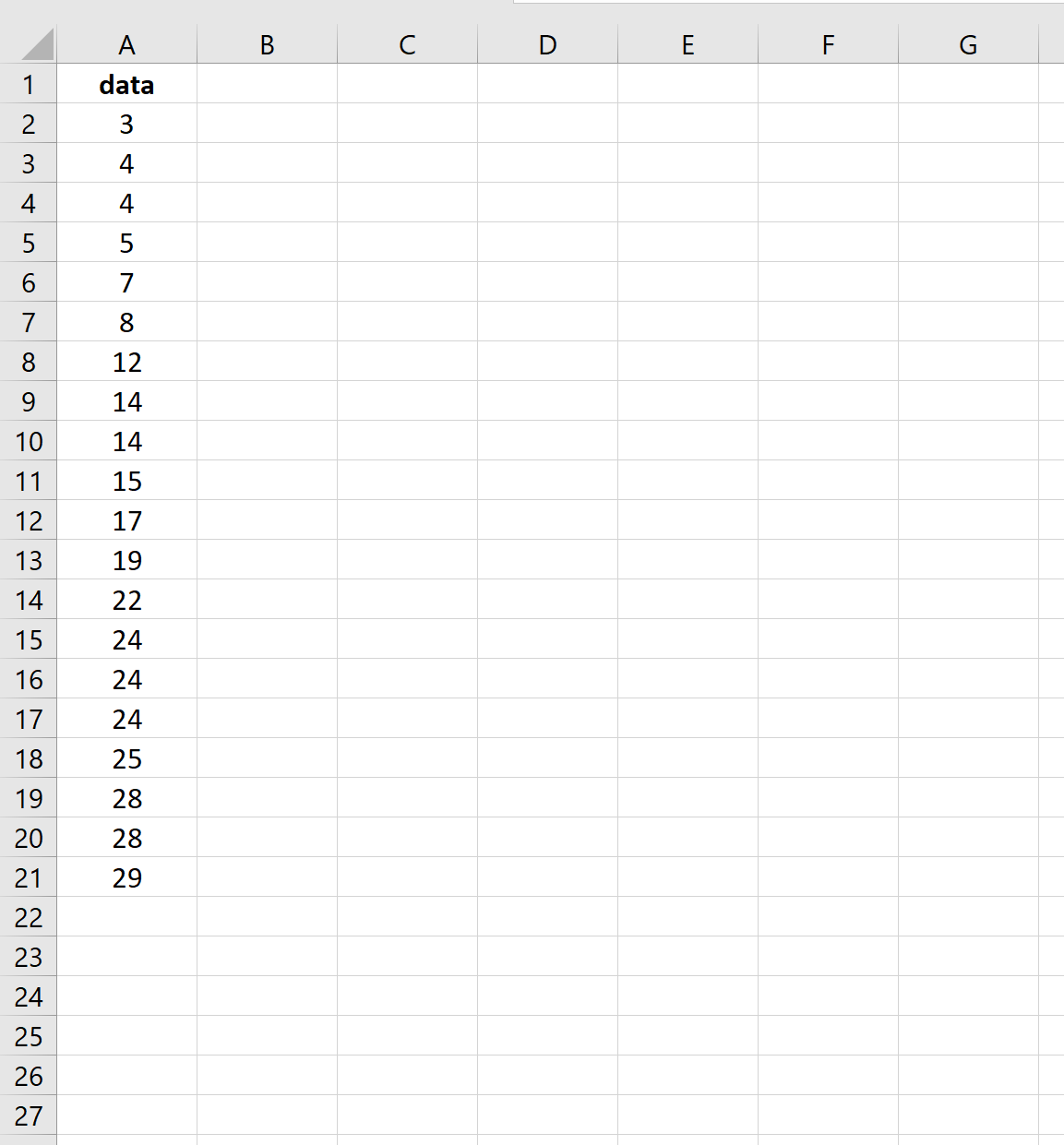
次のスクリーンショットは、このデータ セットの平均の標準誤差を計算する方法を示しています。

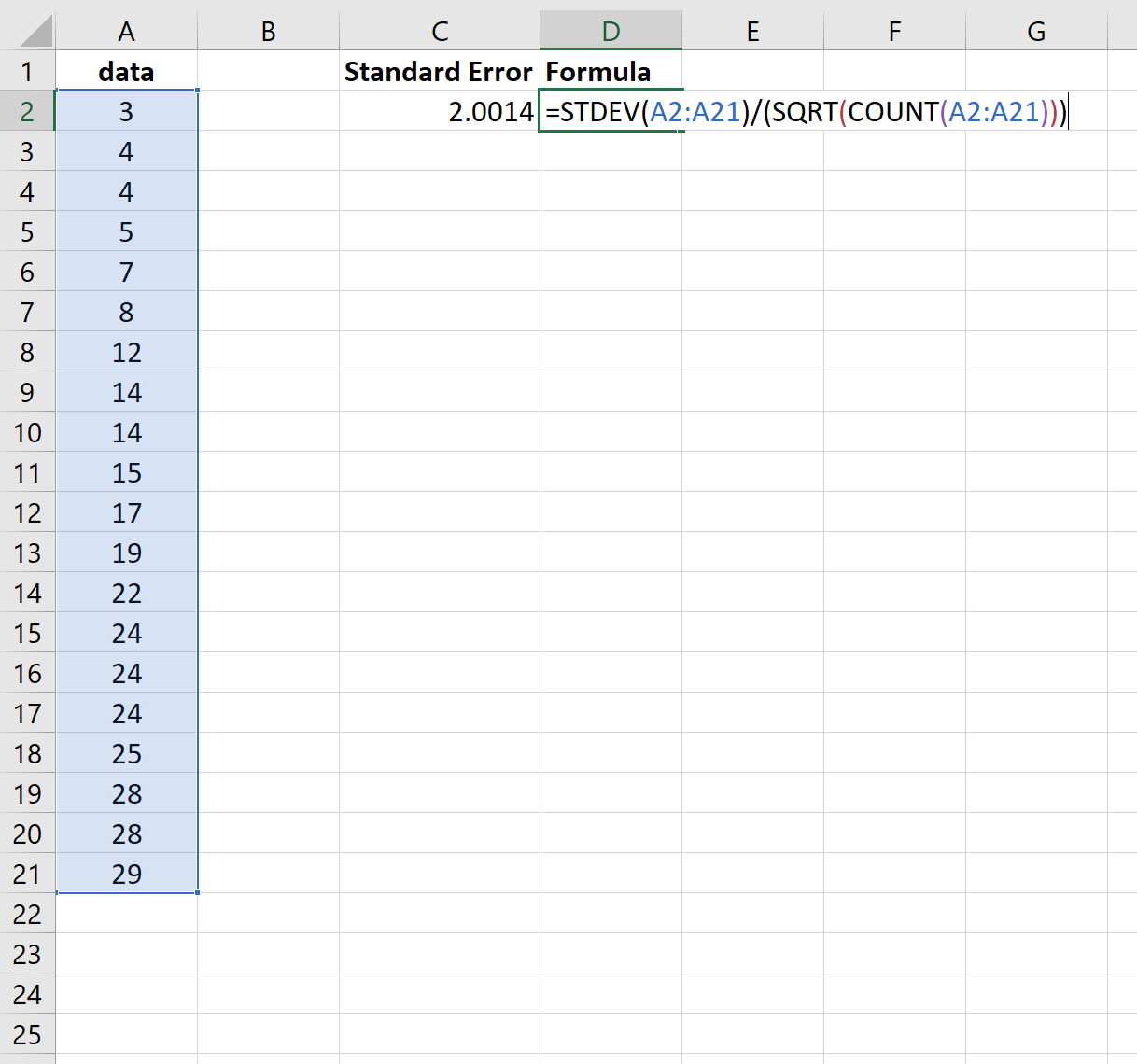
標準誤差は2.0014であることがわかります。

=STDEV()関数はサンプル平均を計算します。これは Excel の=STDEV.S()関数と同等です。

したがって、次の式を使用しても同じ結果が得られます。

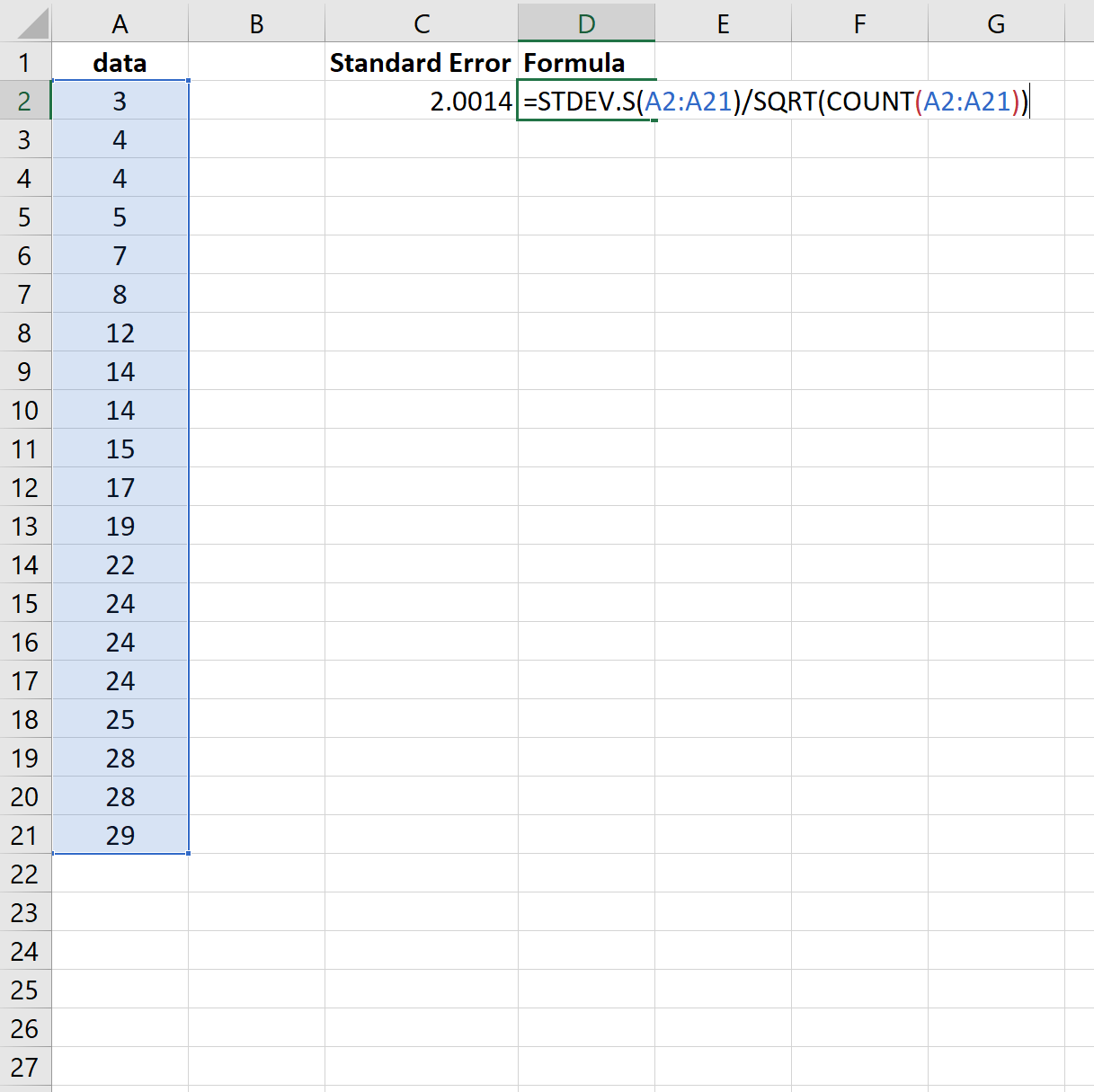
繰り返しますが、標準誤差は2.0014であることがわかります。

平均値の標準誤差を解釈する方法

平均値の標準誤差は、単に平均値の周囲の値の広がりの尺度です。平均値の標準誤差を解釈する際には、次の 2 つの点に留意する必要があります。

1. 平均値の標準誤差が大きいほど、データセット内の値は平均値の周囲にばらつきます。

これを説明するために、前のデータセットの最後の値をさらに大きな数値で変更する場合を考えてみましょう。

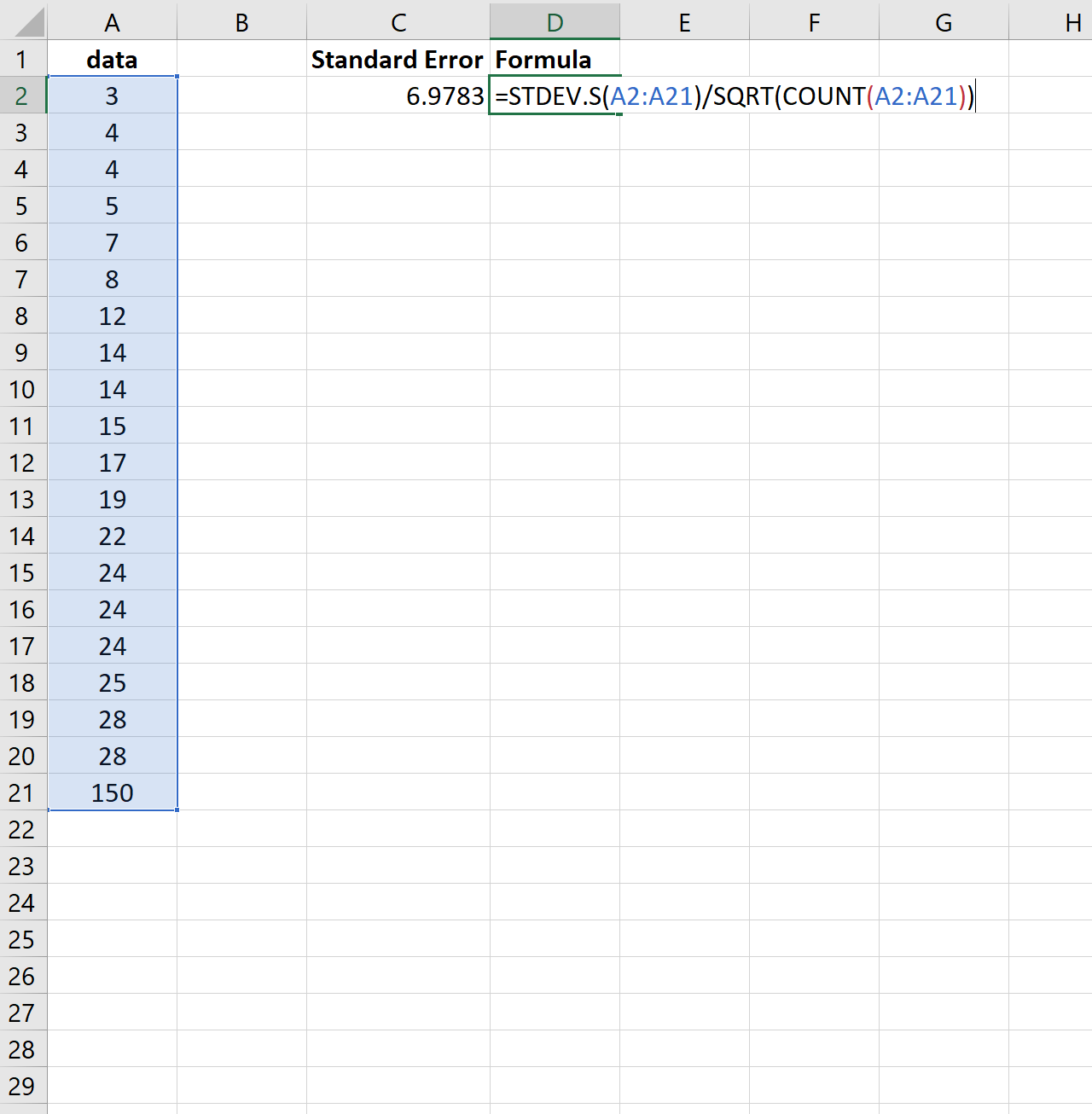
標準誤差が2.0014から6.9783に増加することに注目してください。これは、このデータセットの値が前のデータセットと比較して平均値付近に分散していることを示しています。

2. サンプルサイズが増加するにつれて、平均値の標準誤差は減少する傾向があります。

これを説明するために、次の 2 つのデータセットの平均の標準誤差を考えてみましょう。

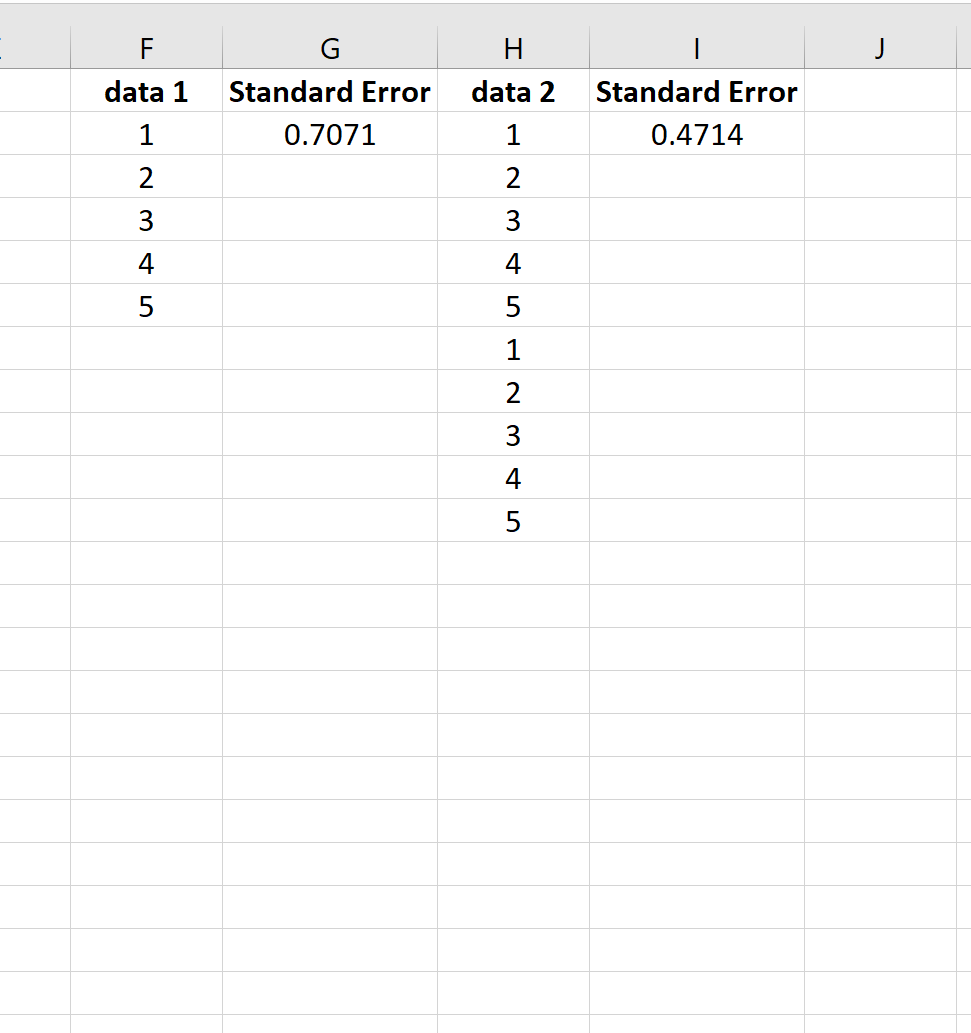
2 番目のデータ セットは、単純に 2 回繰り返された最初のデータ セットです。したがって、両方のデータ セットの平均値は同じですが、2 番目のデータ セットのサンプル サイズが大きいため、標準誤差が小さくなります。