Excel でシェッフェ テストを実行する方法
一元配置分散分析は、 3 つ以上の独立したグループの平均間に統計的に有意な差があるかどうかを判断するために使用されます。
ANOVA 表全体のp 値が一定の有意性レベルを下回っている場合、グループ平均の少なくとも 1 つが他の平均とは異なると言える十分な証拠があります。
ただし、これではどのグループが互いに異なるかは分かりません。これは単に、すべてのグループの平均が等しいわけではないことを示しています。
どのグループが互いに異なっているかを正確に知るには、 ファミリーごとのエラー率を制御できる事後テストを実行する必要があります。
最も一般的に使用される事後テストの 1 つはシェッフェ テストです。
次の段階的な例は、Excel でシェッフェ テストを実行する方法を示しています。
ステップ 1: データを入力する
教師が、3 つの異なる学習方法が生徒間でテストの得点に差をもたらすかどうかを知りたいとします。これをテストするために、彼女は 10 人の生徒をランダムに割り当てて各学習手法を使用させ、試験結果を記録しました。
まず、使用した学習手法に基づいて各生徒の成績を入力します。
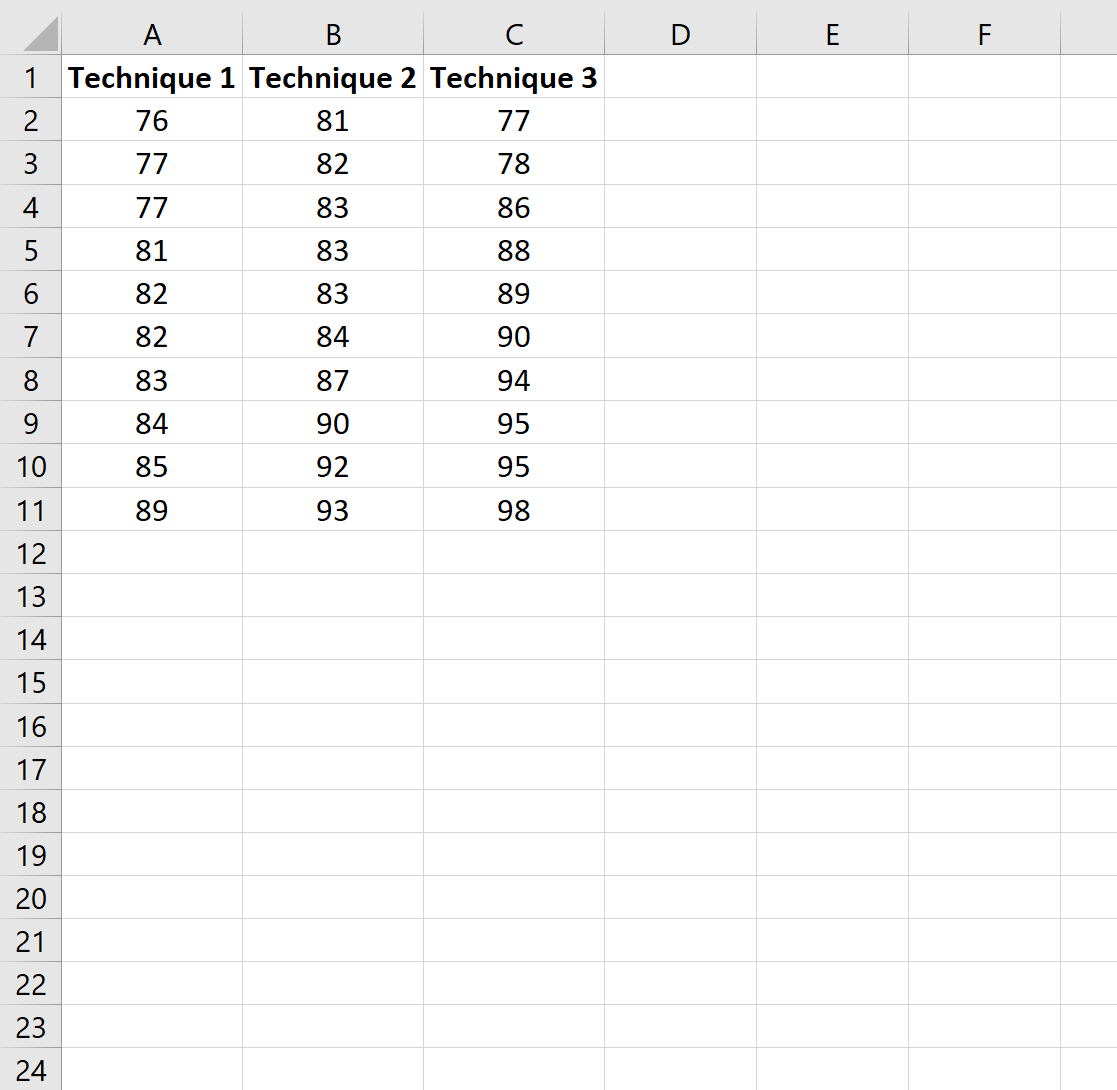
ステップ 2: 一元配置分散分析を実行する
一元配置分散分析を実行するには、上部のリボンに沿って[データ]タブをクリックし、 [分析]グループの[データ分析]オプションをクリックします。

このオプションが表示されない場合は、まずAnalysis ToolPak をロードする必要があります。
表示される新しいウィンドウで、 「Anova: Single Factor」をクリックし、 「OK」をクリックします。
表示される新しいウィンドウで、次の情報を入力します。
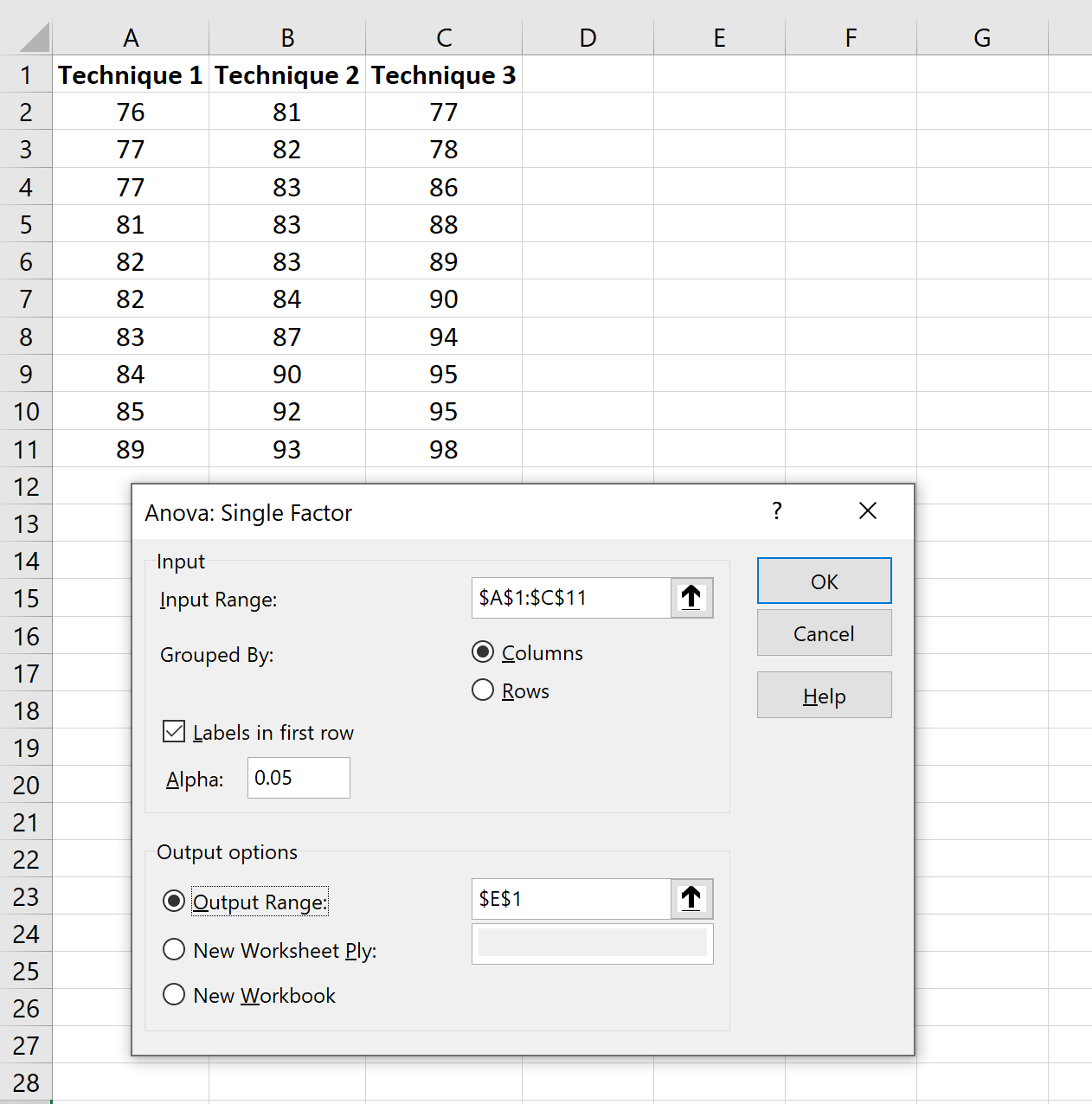
[OK]をクリックすると、一元配置分散分析の結果が表示されます。
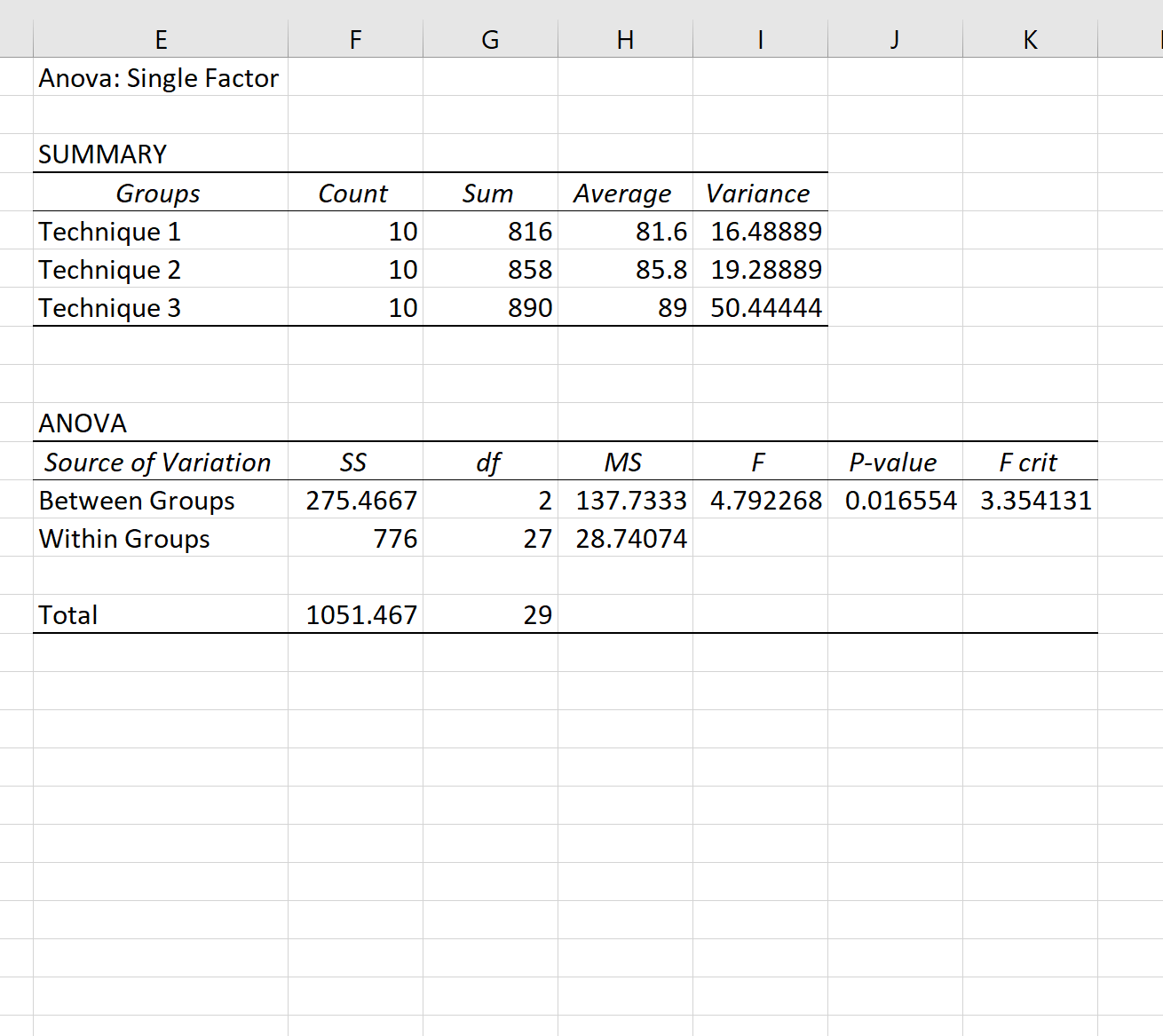
ANOVA 表の全体の p 値 ( 0.016554 ) は 0.05 未満であるため、各グループの試験平均点は同じではないことを意味します。
次に、シェッフェ検定を実行して、どのグループが異なるかを判断します。
ステップ 3: シェッフェ テストを実行する
まず、シェッフェ臨界値を計算する必要があります。これは次のように計算されます。
シェフェ臨界値 = F 臨界値 * 2
この例では、シェッフェ臨界値は 3.354131 * 2 = 6.708です。
次に、各ペア比較の F 統計量を計算できます。これは次のように計算されます。
F 統計量: ( x 1 – x 2 ) 2 / (MS in (1/n 1 + 1/n 2 ))
たとえば、次の式を使用して、各手法間のペアごとの差の F 統計量を計算できます。
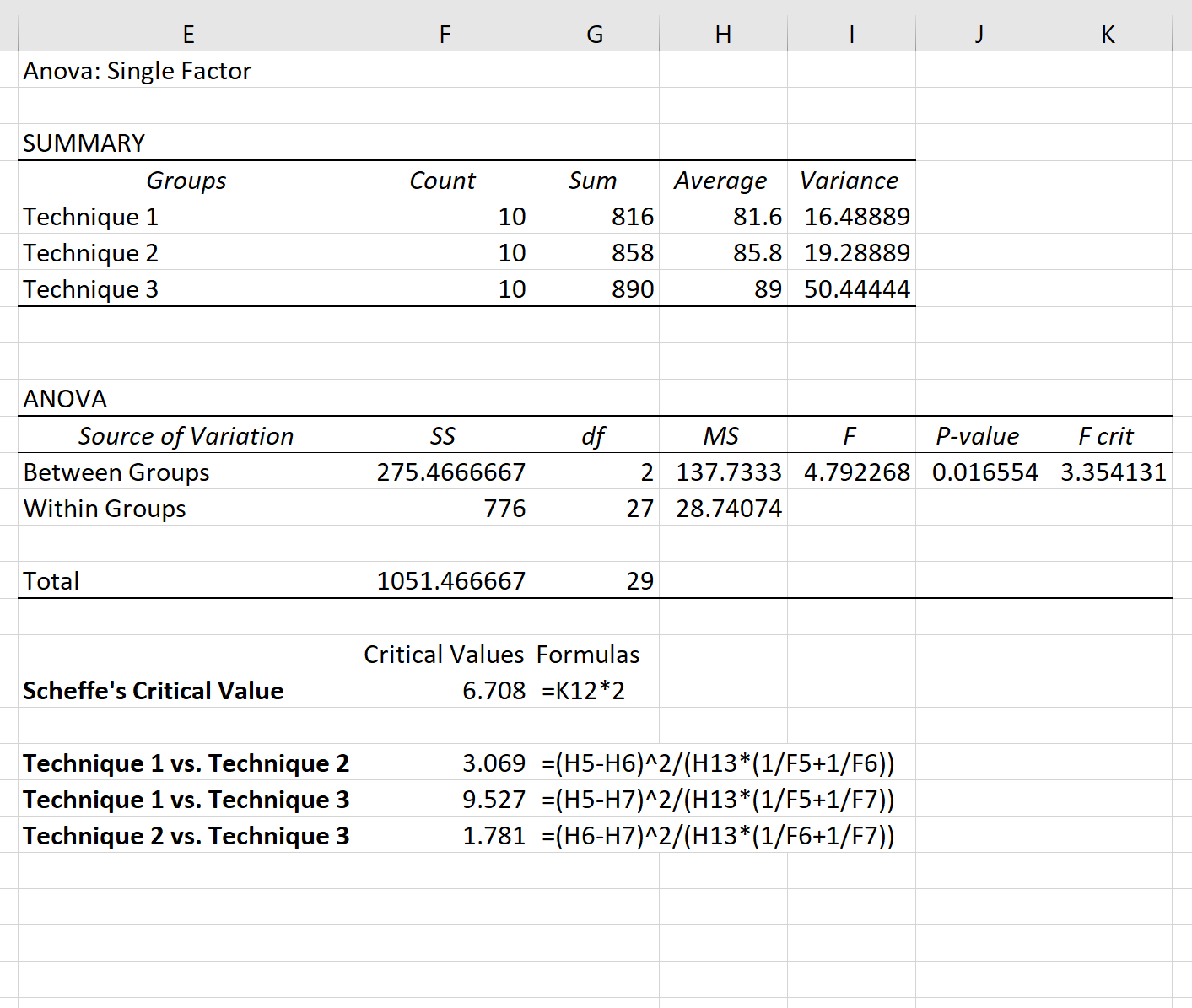
シェッフェ臨界値を超える唯一の F 統計量は、テクニック 1 とテクニック 3 の比較のものです。
したがって、統計的に有意に異なるグループはテクニック 1 とテクニック 3 の 2 つだけです。
追加リソース
Excel で一元配置分散分析を実行する方法
Excel で二元配置分散分析を実行する方法
Excel で Tukey-Kramer 事後テストを実行する方法