カイ二乗分布表の見方

このチュートリアルでは、カイ二乗分布図の読み方と解釈方法を説明します。

カイ二乗分布表とは何ですか?

カイ二乗分布表は、カイ二乗分布の臨界値を示す表です。カイ二乗分布表を使用するには、次の 2 つの値を知っているだけで済みます。

• カイ二乗検定の自由度
• テストのアルファ レベル (一般的な選択肢は 0.01、0.05、および 0.10)

次の図は、カイ二乗分布テーブルの最初の 20 行を示しています。テーブルの左側に自由度が、テーブルの上部にアルファ レベルが示されています。

注:より自由度の高い完全なカイ二乗分布表は、ここで見つけることができます。

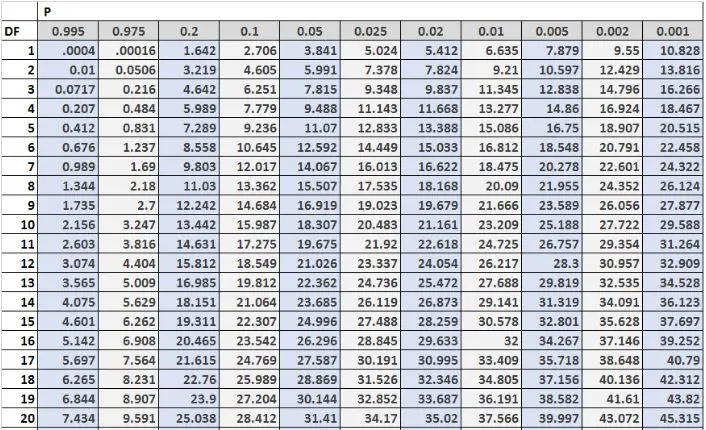
表内の臨界値は、カイ二乗検定の検定統計量と比較されることがよくあります。検定統計量が表にある臨界値より大きい場合は、カイ二乗検定の帰無仮説を棄却し、検定結果が統計的に有意であると結論付けることができます。

カイ二乗分布表の使用例

次の 3 種類のカイ二乗検定でカイ二乗分布表を使用する方法を示します。

• 独立性のカイ二乗検定
• 適合度のカイ二乗検定
• 均一性のカイ二乗検定

独立性のカイ二乗検定

2 つのカテゴリ変数間に有意な関連があるかどうかをテストしたい場合は、独立性のためにカイ二乗検定を使用します。

例:性別が政党の好みと関連しているかどうかを知りたいとします。私たちは 500 人の有権者から単純に無作為にサンプルを採取し、彼らの政党の好みについて尋ねます。有意水準 0.05 を使用して、カイ二乗検定を実行して、性別が政党の好みと関連しているかどうかを判断します。次の表は、調査の結果を示しています。

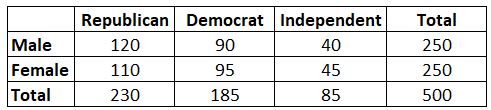
このカイ二乗検定の検定統計量は 0.864 であることがわかります。

次に、カイ二乗分布表で臨界テスト値を見つけることができます。自由度は (#rows-1) * (#columns-1) = (2-1) * (3-1) = 2 に等しく、この問題ではアルファ レベル 0.05 を使用する必要があることがわかりました。カイ二乗分布表によると、検定の臨界値は5.991です。

検定統計量が臨界値より小さいため、帰無仮説を棄却できません。これは、性別と政党の好みの間に関連性があると言える十分な証拠がないことを意味します。

適合度のカイ二乗検定

カテゴリ変数が仮説分布に従うかどうかをテストしたい場合は、カイ二乗適合度検定を使用します。

例:ある店主は、週末の顧客の 30% が金曜日に来店し、土曜日に 50%、日曜日に 20% が来店すると述べています。独立した研究者がランダムな週末にその店を訪れ、金曜日には 91 人、土曜日には 104 人、日曜日には 65 人の顧客がいることを発見しました。有意水準 0.10 を使用して、カイ二乗検定を実行して適合度をチェックし、データが店主の主張と一致しているかどうかを判断します。

この場合、検定統計量は 10,616 であることがわかります。

次に、カイ二乗分布表で臨界テスト値を見つけることができます。自由度は (#outcomes-1) = 3-1 = 2 に等しく、問題はアルファ レベル 0.10 を使用する必要があることを示しています。したがって、カイ二乗分布表によれば、検定の臨界値は4.605です。

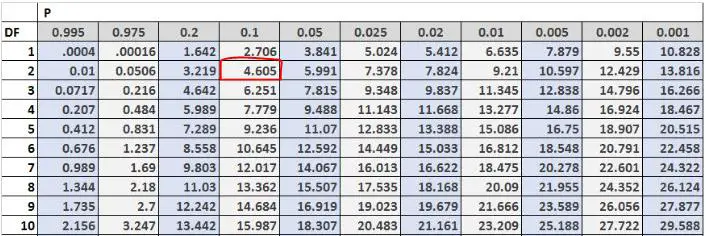
検定統計量が臨界値より大きいため、帰無仮説を棄却します。これは、週末にこの店に来る顧客の実際の分布が金曜日に 30%、土曜日に 50%、日曜日に 20% に等しくないと言える十分な証拠があることを意味します。

均一性のカイ二乗検定

複数のグループ間に比率の差があるかどうかを正式に検定したい場合は、均一性のカイ二乗検定を使用します。

例:バスケットボールのトレーニング センターは、2 つの新しいトレーニング プログラムにより、難しい射撃テストに合格する選手の割合が向上するかどうかを確認したいと考えています。 172 人のプレーヤーがプログラム 1 に、173 人がプログラム 2 に、215 人が現在のプログラムにランダムに割り当てられます。 1 か月間トレーニング プログラムを使用した後、選手は射撃テストを受けます。以下の表は、使用したプログラムに基づいて射撃テストに合格したプレーヤーの数を示しています。

有意水準 0.05 を使用してカイ二乗検定を実行し、各トレーニング プログラムの成功率が同じかどうかを判断します。

このカイ二乗検定の検定統計量は 4.208 であることがわかります。

次に、カイ二乗分布表で臨界テスト値を見つけることができます。自由度は (#rows-1) * (#columns-1) = (2-1) * (3-1) = 2 に等しく、この問題ではアルファ レベル 0.05 を使用する必要があることがわかりました。カイ二乗分布表によると、検定の臨界値は5.991です。

検定統計量が臨界値より小さいため、帰無仮説を棄却できません。これは、3 つのトレーニング プログラムが異なる結果を生み出すと言える十分な証拠がないことを意味します。