カイ二乗検定を実際に使用する 4 つの例
統計学では、次の 2 種類のカイ二乗検定があります。
1. カイ二乗適合度検定– カテゴリ変数が仮説分布に従うかどうかを判断するために使用されます。
2.独立性のカイ二乗検定– 2 つのカテゴリ変数間に有意な関連性があるかどうかを判断するために使用されます。
この記事では、これらのタイプのカイ二乗検定が実際の状況でどのように使用されるかを示すいくつかの例を紹介します。
例 1: カイ二乗適合度検定
店主が、毎日同じ数の顧客が店に来ると主張するとします。
この仮説を検証するために、彼は特定の週に来店する顧客の数を記録し、次のことを発見しました。
- 月曜日: 50 人の顧客
- 火曜日:お客様60名
- 水曜日:お客様40名
- 木曜日:お客様47名
- 金曜日: 53名のお客様
彼は、カイ二乗適合度検定を使用して、毎日来店する顧客の分布が分布仮説と一致しているかどうかを判断できます。
カイ二乗適合度検定計算ツールを使用すると、検定の p 値が0.359であることがわかります。
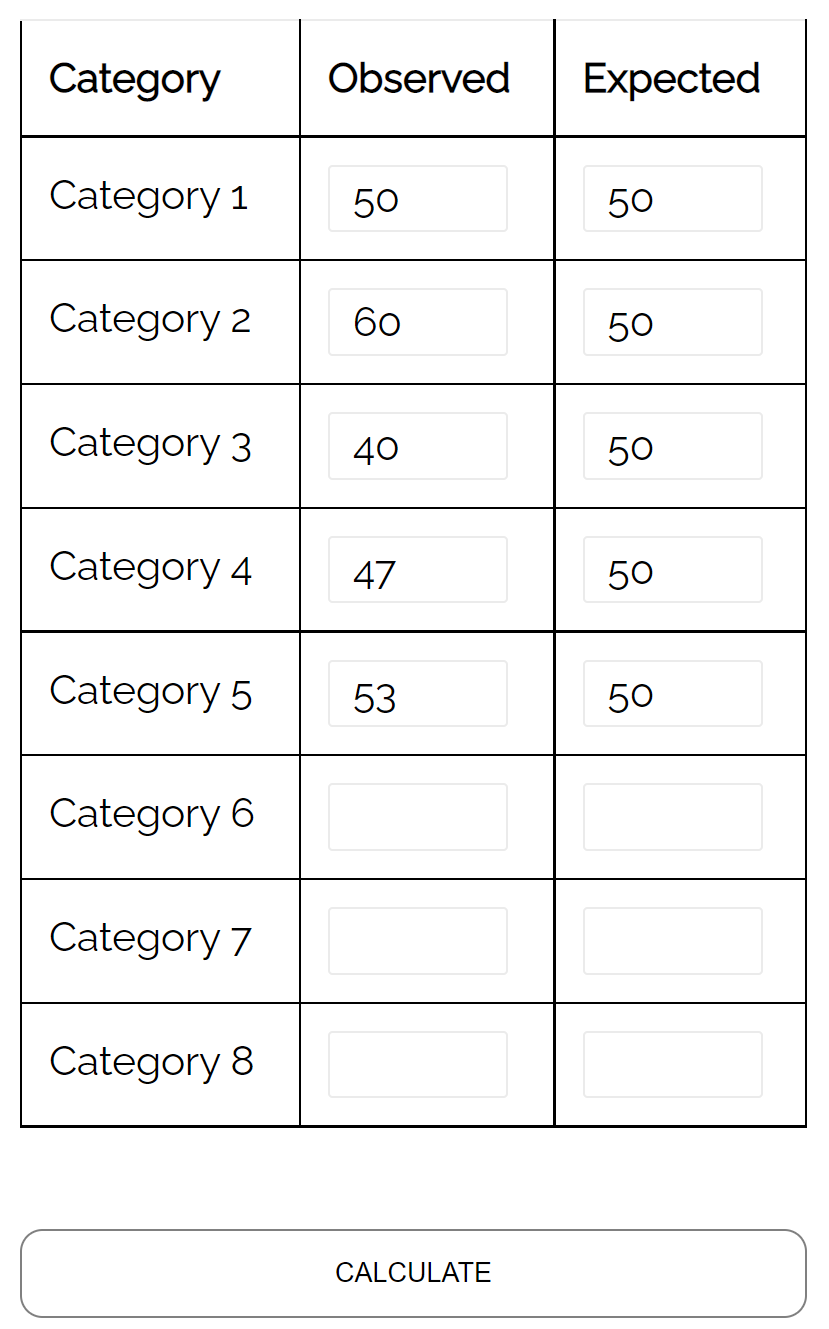

この p 値は 0.05 未満ではないため、顧客の真の分布が店舗所有者が主張するものと異なると主張する十分な証拠はありません。
例 2: カイ二乗適合度検定
ある生物学者が、毎週、同じ数の 4 種類のシカが森林の特定の樹林帯に侵入すると主張したとします。
この仮説を検証するために、彼女は 1 週間にわたって森林地帯に入ってきたシカの種類ごとの数を記録しました。
- 種 #1: 22
- 種 #2: 20
- 種 #3: 23
- 種 #4: 35
彼女は、カイ二乗適合度検定を使用して、森林の樹林帯に毎週入るシカの種の分布がその仮説の分布と一致しているかどうかを判断できます。
カイ二乗適合度検定計算ツールを使用すると、検定の p 値が0.137であることがわかります。
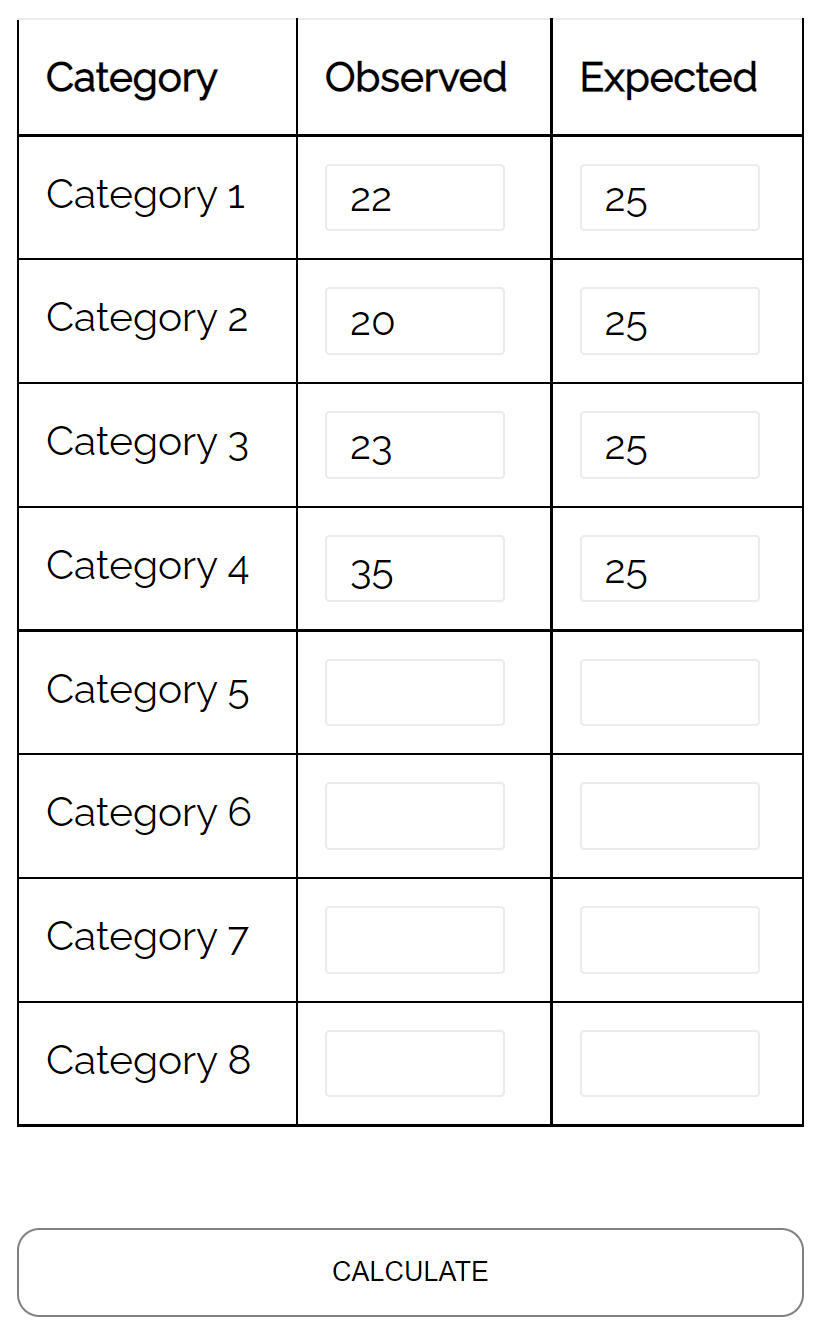
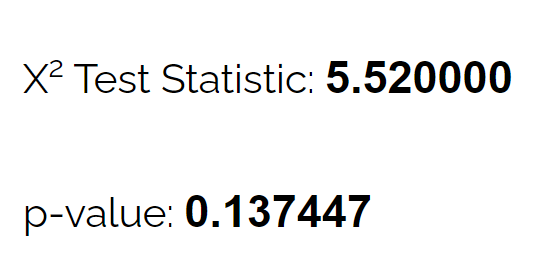
この p 値は 0.05 未満ではないため、シカの真の分布が生物学者が主張するものと異なると主張する十分な証拠はありません。
例 3: カイ二乗独立性検定
ある都市の政策立案者が、性別が政党の好みに関連しているかどうかを知りたいと考えているとします。
彼は、500 人の有権者から単純に無作為にサンプルを抽出し、政党の好みについて尋ねることにしました。次の表は、調査の結果を示しています。
| 共和党 | 民主党 | 独立した | 合計 | |
| 男 | 120 | 90 | 40 | 250 |
| 女性 | 110 | 95 | 45 | 250 |
| 合計 | 230 | 185 | 85 | 500 |
独立性のカイ二乗検定を使用して、2 つの変数間に統計的に有意な関連があるかどうかを判断できます。
カイ二乗独立性検定計算機を使用すると、検定の p 値が0.649であることがわかります。
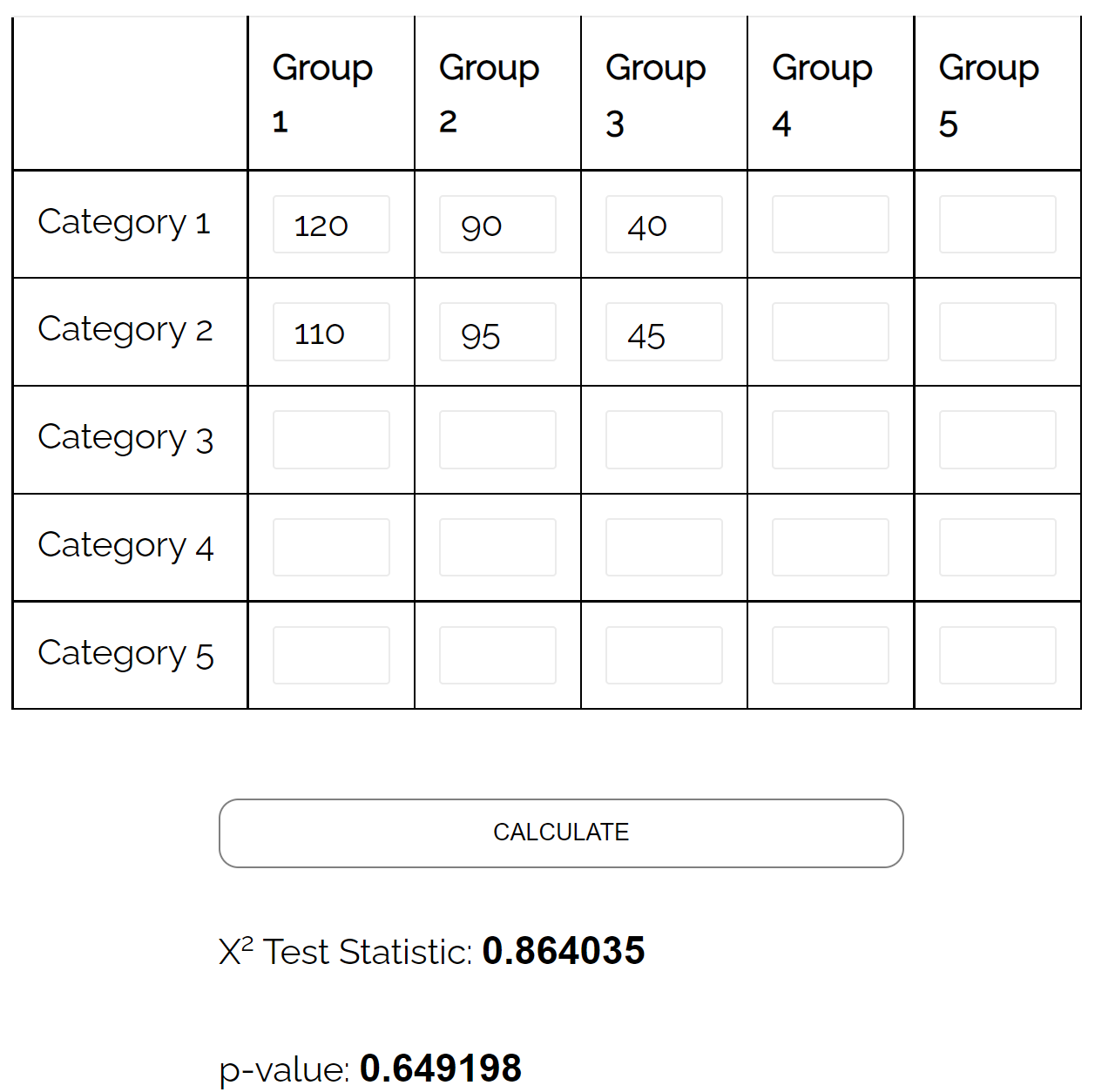
p 値は 0.05 未満ではないため、性別と政党の好みの間に関連があると言う十分な証拠はありません。
例 4: カイ二乗独立性検定
研究者が、婚姻状況が学歴と関連しているかどうかを知りたいと考えているとします。
彼は 300 人の単純な無作為サンプルを採取することにし、次の結果を得ました。
| 高校 | 学士 | マスター以上 | 合計 | |
| 既婚 | 20 | 100 | 35 | 155 |
| 学士 | 50 | 80 | 15 | 145 |
| 合計 | 70 | 180 | 50 | 300 |
独立性のカイ二乗検定を使用して、2 つの変数間に統計的に有意な関連があるかどうかを判断できます。
カイ二乗独立性検定計算機を使用すると、検定の p 値が0.000011であることがわかります。
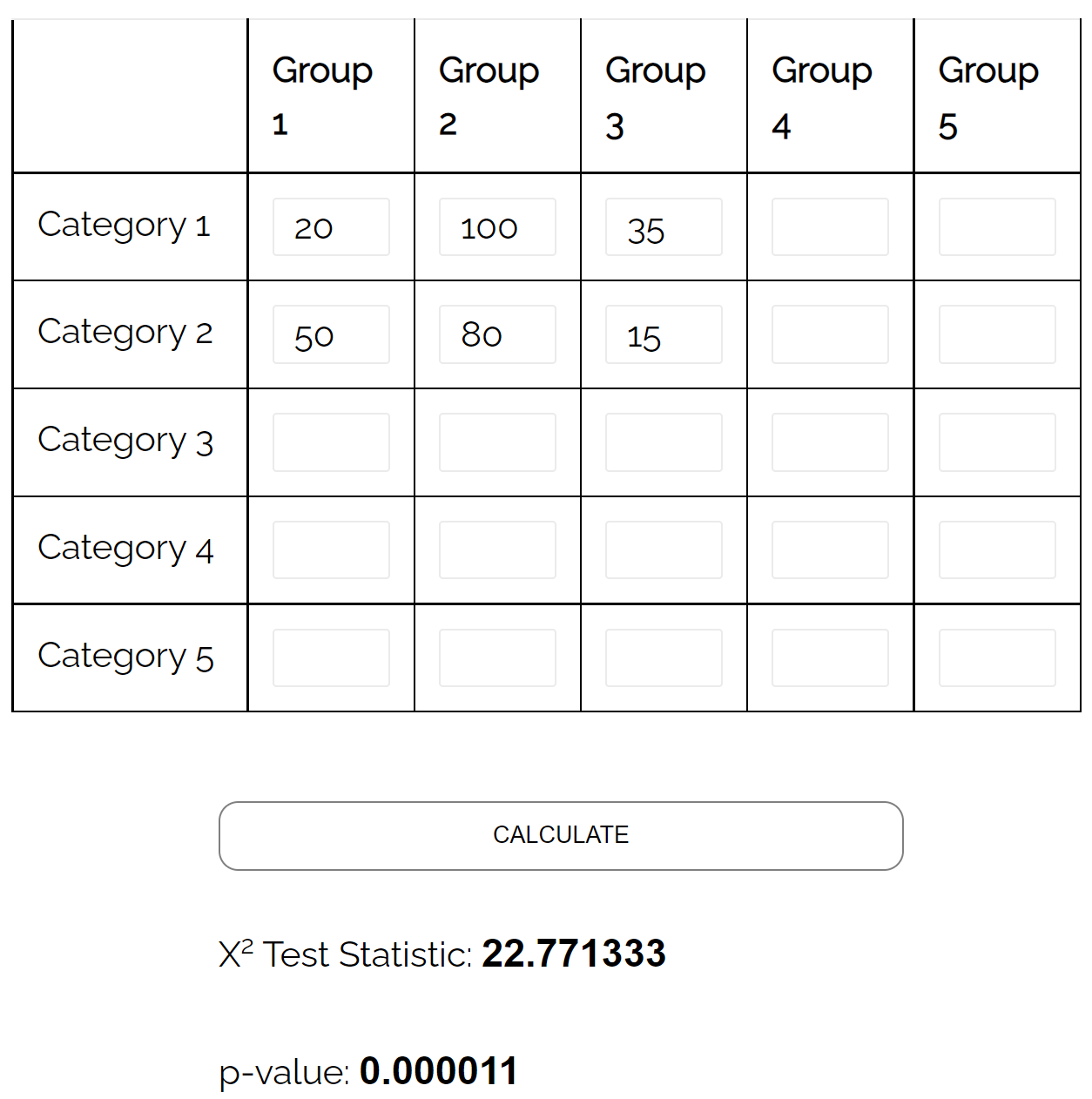
p 値は 0.05 未満であるため、婚姻状況と教育レベルの間に関連があると言える十分な証拠があります。
追加リソース
次のチュートリアルでは、さまざまな種類のカイ 2 乗検定の概要を説明します。
次のチュートリアルでは、カイ二乗検定と他の統計検定の違いについて説明します。