Excel でカイ二乗独立性検定を実行する方法

独立性のカイ二乗検定は、 2 つのカテゴリ変数間に有意な関連があるかどうかを判断するために使用されます。

このチュートリアルでは、Excel で独立性のカイ二乗検定を実行する方法を説明します。

例: Excel でのカイ二乗独立性検定

性別が政党の好みと関連しているかどうかを知りたいとします。私たちは 500 人の有権者から単純に無作為にサンプルを採取し、彼らの政党の好みについて尋ねます。次の表は、調査の結果を示しています。

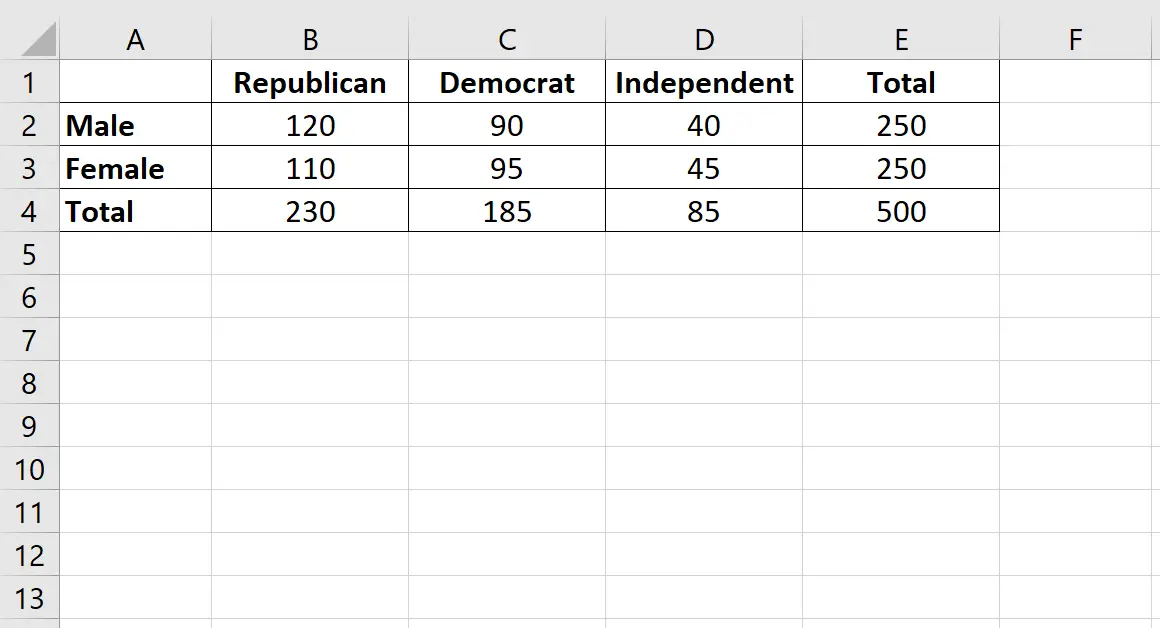
次の手順を使用して独立性のカイ二乗検定を実行し、性別が政党の好みに関連しているかどうかを判断します。

ステップ 1: 前提条件を定義します。

次の仮定を使用して、独立性のカイ二乗検定を実行します。

• H ₀ :性別と政党の好みは独立しています。
• H ₁ :性別と政党の好みは独立していません。

ステップ 2: 期待値を計算します。

次に、次の式を使用して分割表の各セルの期待値を計算します。

期待値 = (行の合計 * 列の合計) / テーブルの合計。

たとえば、共和党員男性の期待値は (230*250) / 500 = 115です。

この式を繰り返すと、テーブルの各セルの期待値を取得できます。

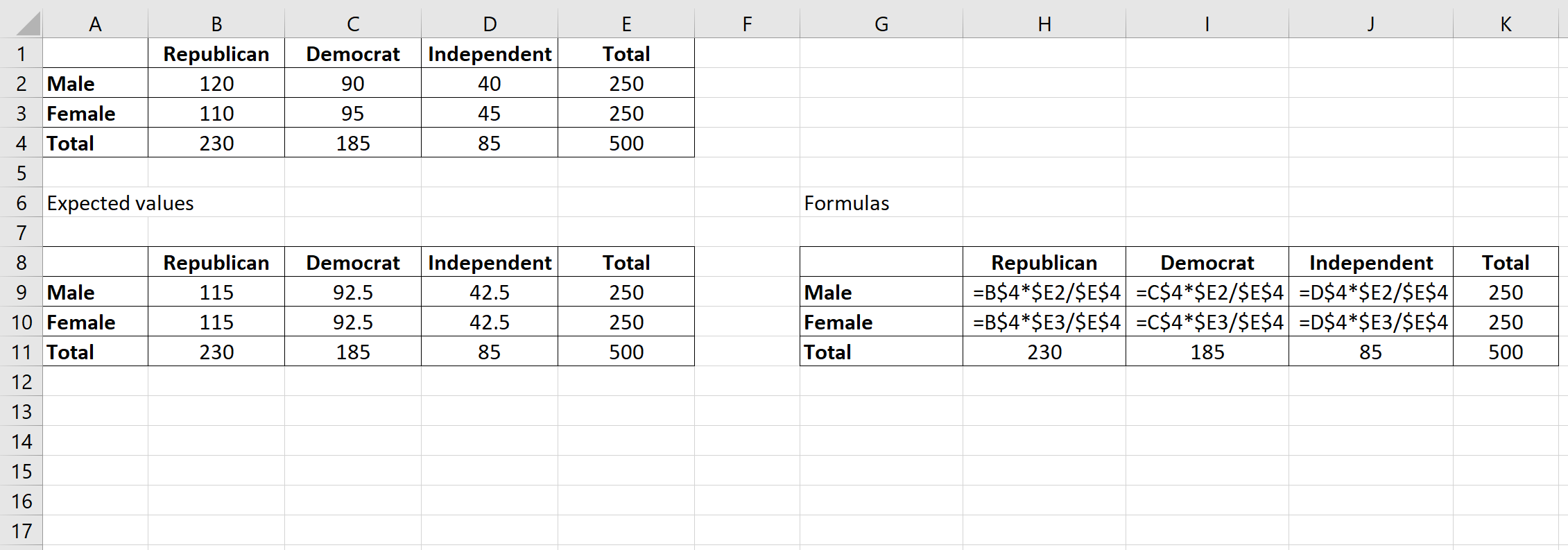
ステップ 3: テーブル内の各セルについて (OE) ² /E を計算します。

次に、テーブル内の各セルに対して(OE) ² /Eを計算します。ここで、

• ○：実測値
• E:期待値

たとえば、男性の共和党員の値は (120-115) ² /115 = 0.2174になります。

テーブル内のセルごとにこの式を繰り返すことができます。

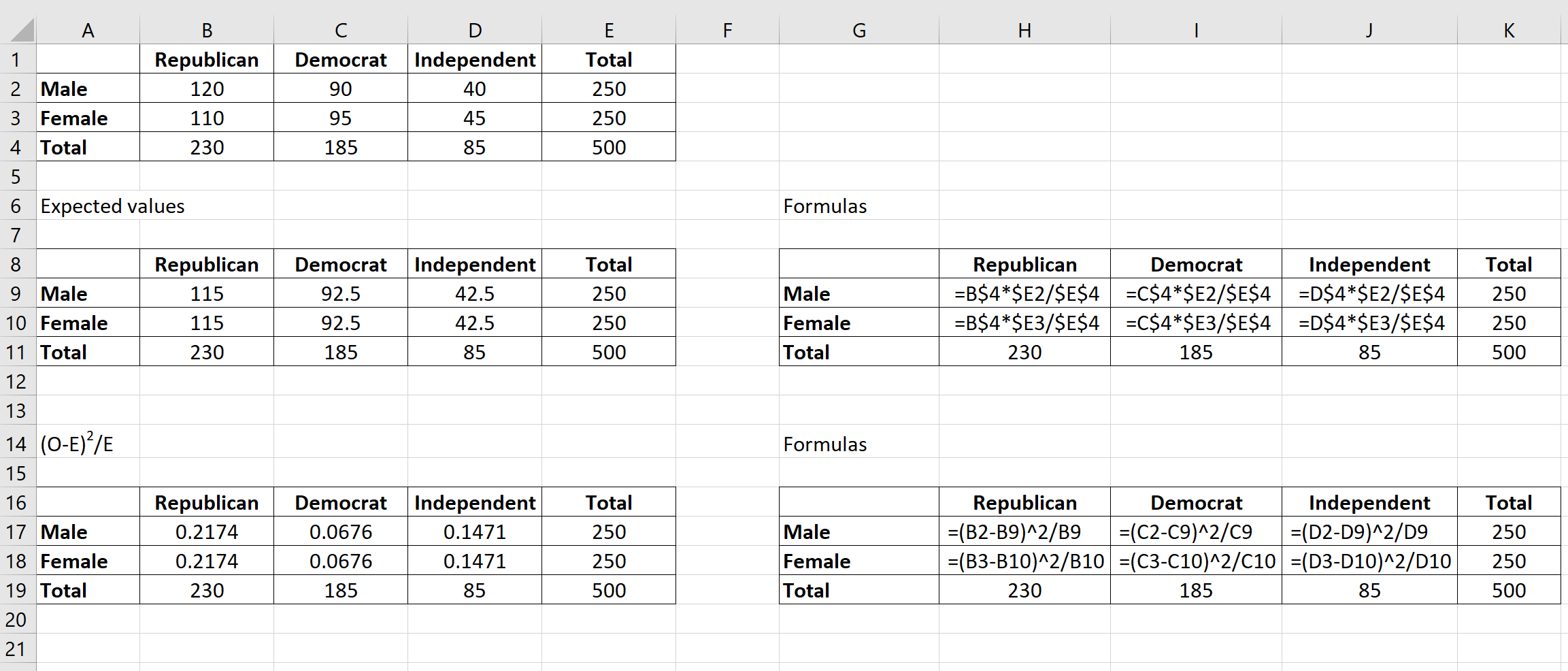
ステップ 4: 検定統計量^X2と対応する p 値を計算します。

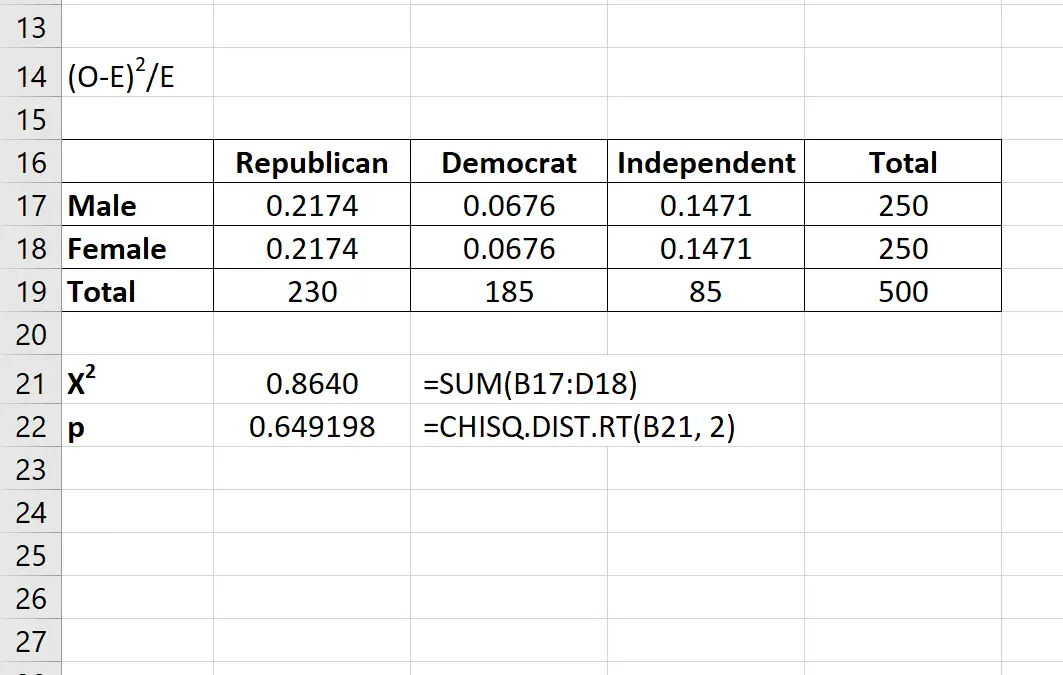
検定統計量^{X2 は、}最後の表の値の単純な合計です。

検定統計量 X ²に対応する p 値は、次の式を使用して求めることができます。

=CHISQ.DIST.RT(x, 自由度)

金：

• x:検定^統計量
• deg_freedom:自由度、次のように計算されます: (#rows-1) * (#columns-1)

検定統計量^{X2 は}0.8640で、対応する p 値は0.649198であることがわかります。

ステップ 5: 結論を導き出します。

この p 値は 0.05 未満ではないため、帰無仮説を棄却できません。これは、性別と政党の好みの間に関連性があると言える十分な証拠がないことを意味します。

注: カイ二乗独立検定計算機を使用してこの検定全体を実行することもできます。