Excel でカイ 2 乗適合検定を実行する方法

カイ二乗適合度検定は、カテゴリ変数が仮説分布に従うかどうかを判断するために使用されます。

このチュートリアルでは、Excel でカイ二乗適合度検定を実行する方法について説明します。

例: Excel でのカイ二乗適合度検定

店主は、毎日同じ数の顧客が店に来ると言いました。この仮説を検証するために、独立した研究者が特定の週に店舗に来店する顧客の数を記録し、次のことを発見しました。

• 月曜日: 50 人の顧客
• 火曜日：お客様60名
• 水曜日：お客様40名
• 木曜日：お客様47名
• 金曜日： 53名のお客様

次の手順を使用してカイ二乗適合度検定を実行し、データが店舗所有者の主張と一致しているかどうかを判断します。

ステップ 1: データを入力します。

まず、1 つの列に毎日の予想顧客数のデータ値を入力し、別の列に毎日観測された顧客数のデータ値を入力します。

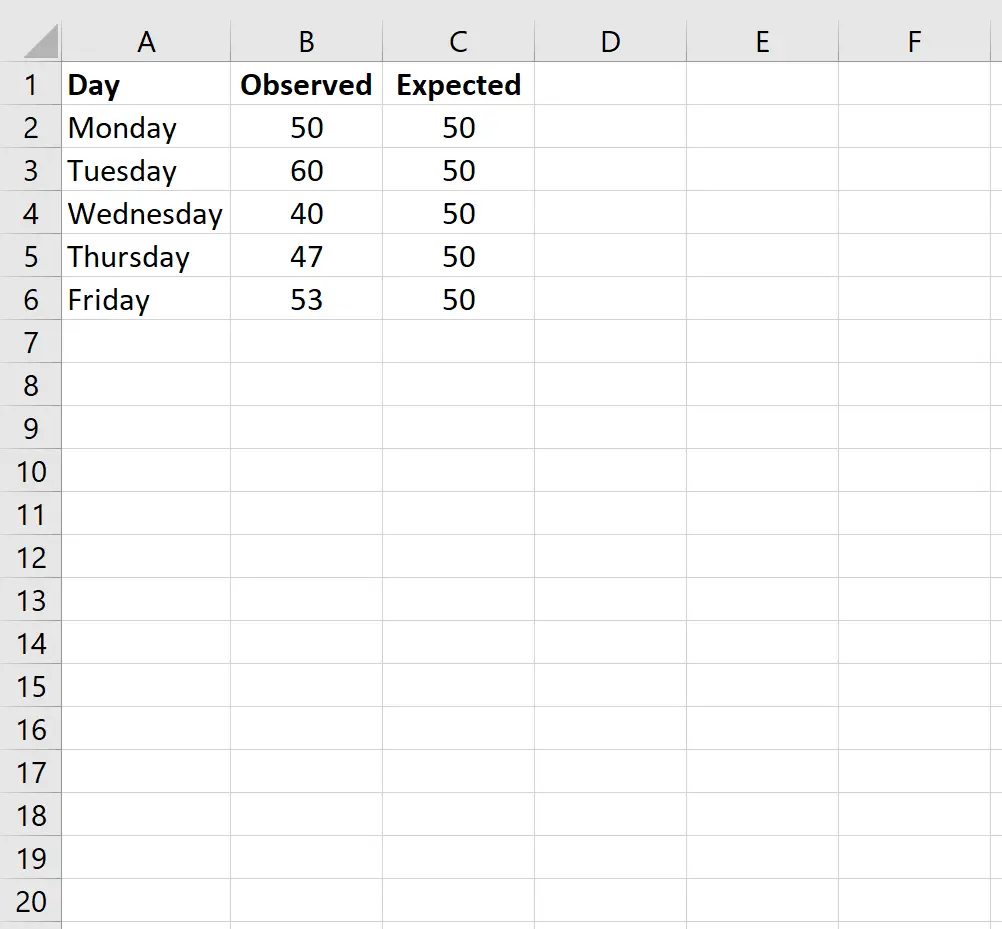
注:顧客は合計 250 人でした。したがって、店主が毎日同じ数の顧客が店に入ると予想する場合、1 日あたり 50 人の顧客がいることを期待することになります。

ステップ 2: 観測値と期待値の差を見つけます。

適合度検定のカイ二乗検定統計量は、X ² = Σ(OE) ² / Eです。

金：

• Σ： 「和」を意味する派手な記号
• ○：実測値
• E:期待値

次の式は、各行の(OE) ² /Eを計算する方法を示しています。

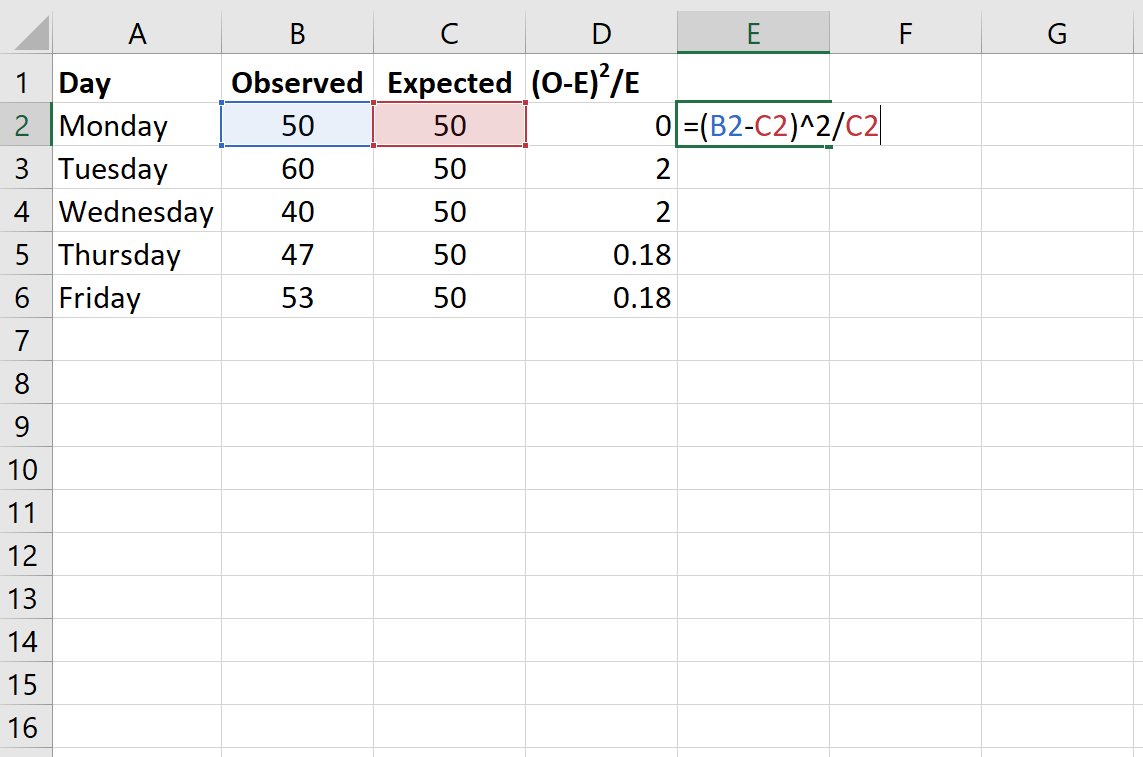
ステップ 3: カイ二乗検定統計量と対応する p 値を計算します。

最後に、次の式を使用して、カイ二乗検定統計量と対応する p 値を計算します。

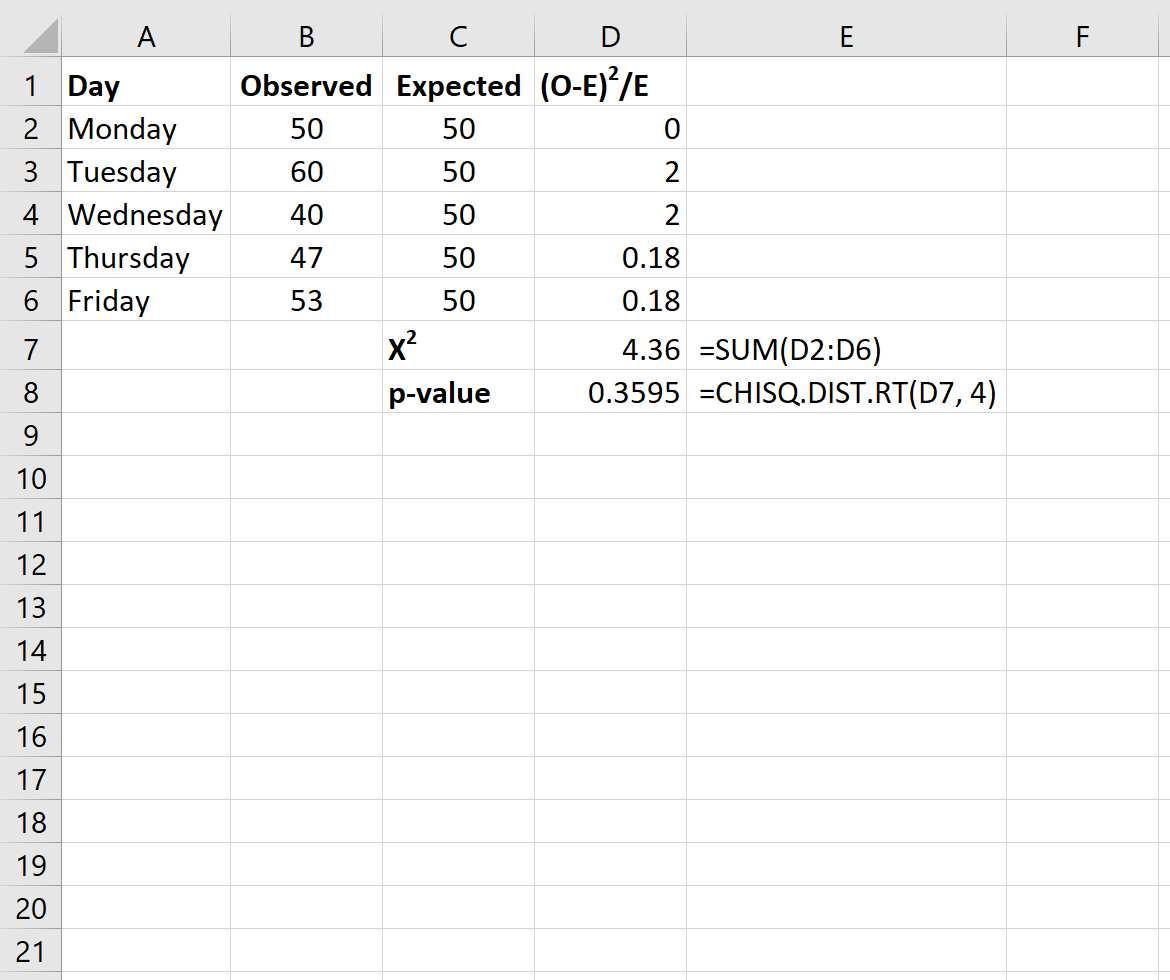
注: Excel 関数CHISQ.DIST.RT(x, deg_freedom) は、検定統計量xと特定の自由度に関連付けられたカイ二乗分布の正しい確率を返します。自由度は n-1 として計算されます。この場合、deg_freedom = 5 – 1 = 4 となります。

ステップ 4: 結果を解釈します。

この検定の^X2検定統計量は4.36で、対応する p 値は0.3595です。この p 値は 0.05 未満ではないため、帰無仮説を棄却できません。これは、顧客の本当の分布が店主が報告したものと異なると言える十分な証拠がないことを意味します。