カテゴリ分布とは何ですか?
カテゴリ分布は、確率変数がKカテゴリの 1 つに属する値を取る確率を記述する離散確率分布であり、各カテゴリは確率に関連付けられています。
分布がカテゴリ分布として分類されるには、次の基準を満たしている必要があります。
- カテゴリは個別です。
- 2 つ以上のカテゴリが考えられます。
- 確率変数が各カテゴリの値を取る確率は 0 から 1 の間でなければなりません。
- すべてのカテゴリの確率の合計は 1 になる必要があります。
カテゴリ分布の最も明白な例は、サイコロを振ることに関連する出目の分布です。 K = 6 個の潜在的な結果があり、各結果の確率は 1/6 です。
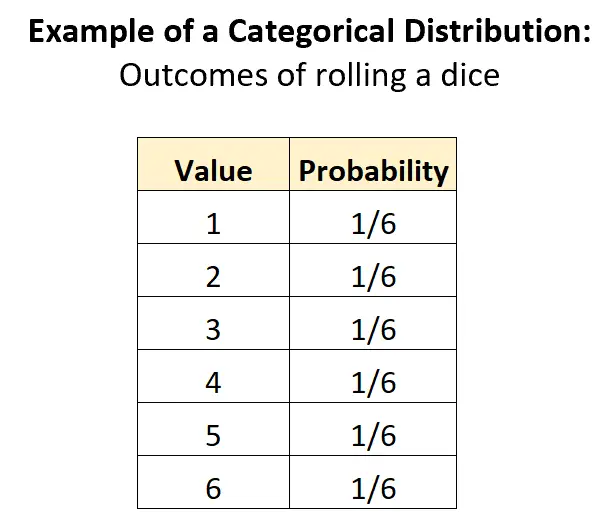
この分布は、カテゴリ分布として分類される基準をすべて満たしています。
- カテゴリは離散的です (たとえば、確率変数は離散値 – 1、2、3、4、5、6 のみを取ることができます)
- 2 つ以上のカテゴリが考えられます。
- 各カテゴリの確率は 0 から 1 の間です。
- 確率の合計は 1 になります: 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1。
原則:
結果の数を数えることができる場合は、離散確率変数を操作していることになります。たとえば、コインが表になった回数を数えることになります。
しかし、結果を測定できれば、連続確率変数を扱うことになります (たとえば、身長、体重、時間などを測定するなど)。
カテゴリ分布のその他の例
現実世界には次のような多くのカテゴリ分布があります。
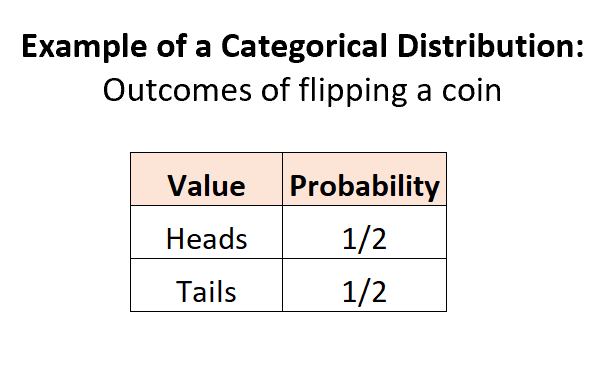
例 1: コインを投げます。
コインを投げると、2 つの離散的な結果が得られる可能性があり、各結果の確率は 0 から 1 の間で、確率の合計は 1 に等しくなります。
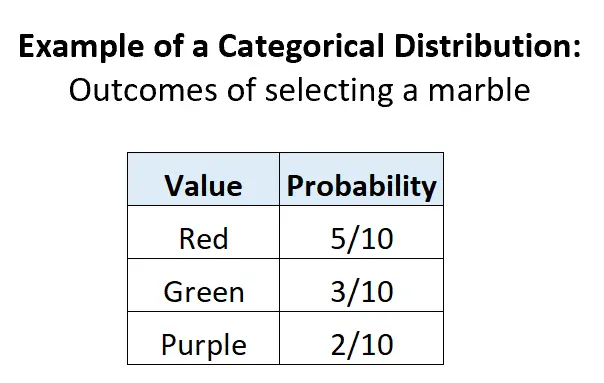
例 2: 壺の中の大理石の選択。
壺に赤いビー玉が 5 個、緑のビー玉が 3 個、紫のビー玉が 2 個入っているとします。壺からボールをランダムに選択した場合、3 つの潜在的な個別の結果があり、各結果の確率は 0 から 1 の間で、確率の合計は 1 に等しくなります。
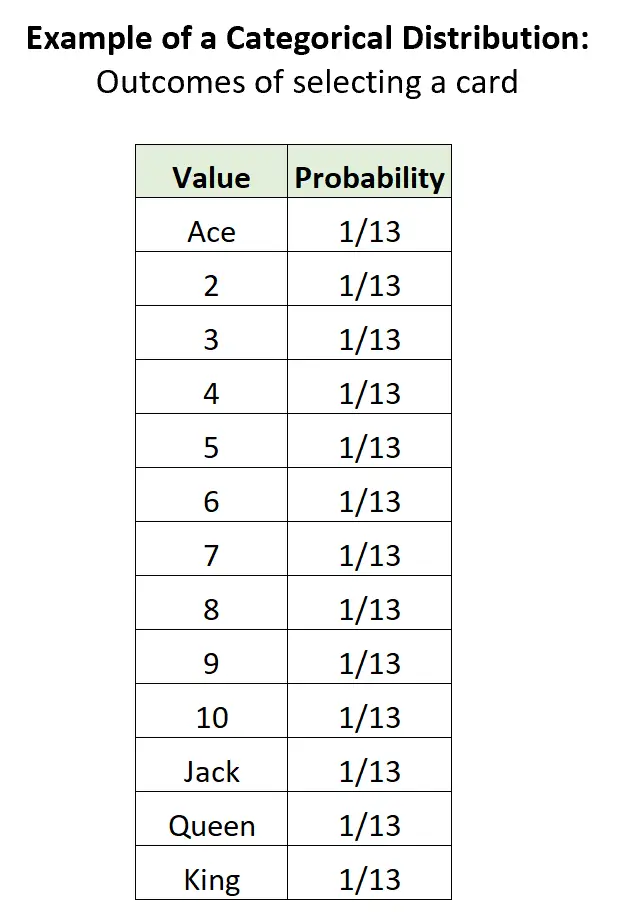
例 3: デッキからカードを選択する。
52 枚のカードからなる標準的なデッキからカードをランダムに選択した場合、13 個の個別の結果が考えられ、各結果の確率は 0 から 1 の間であり、確率の合計は 1 に等しくなります。
他のディストリビューションとの関係
分布がカテゴリ分布として分類されるには、 K ≥ 2 の潜在的な結果とn = 1 試行が必要です。
この用語を使用すると、カテゴリ分布は次の分布と似ています。
ベルヌーイ分布: K = 2 結果、 n = 1 検定
二項分布: K = 2 エンドポイント、n ≥ 1 試験
多項分布: K ≥ 2 結果、n ≥ 試行