Python でクック距離を計算する方法
クック距離は、回帰モデルで影響力のある観測値を特定するために使用されます。
クック距離の公式は次のとおりです。
d i = (ri 2 / p*MSE) * (h ii / (1- h ii ) 2 )
金:
- r iは i番目の剰余です
- pは回帰モデルの係数の数です。
- MSE は平均二乗誤差です
- h iiはi 番目のレバレッジ値です
基本的に、クック距離は、i番目の観測値が削除されたときにモデルのすべての近似値がどの程度変化するかを測定します。
クック距離の値が大きいほど、特定の観測値の影響力は大きくなります。
一般に、クック距離が 4/n ( n = 観測値の合計) より大きい観測値は、大きな影響を与えていると見なされます。
このチュートリアルでは、Python で特定の回帰モデルのクック距離を計算する方法を段階的に説明します。
ステップ 1: データを入力する
まず、Python で操作するための小さなデータセットを作成します。
import pandas as pd #create dataset df = pd. DataFrame ({' x ': [8, 12, 12, 13, 14, 16, 17, 22, 24, 26, 29, 30], ' y ': [41, 42, 39, 37, 35, 39, 45, 46, 39, 49, 55, 57]})
ステップ 2: 回帰モデルを当てはめる
次に、 単純な線形回帰モデルを当てはめます。
import statsmodels. api as sm
#define response variable
y = df[' y ']
#define explanatory variable
x = df[' x ']
#add constant to predictor variables
x = sm. add_constant (x)
#fit linear regression model
model = sm. OLS (y,x). fit ()
ステップ 3: 調理距離を計算する
次に、モデル内の各観測値のクック距離を計算します。
#suppress scientific notation
import numpy as np
n.p. set_printoptions (suppress= True )
#create instance of influence
influence = model. get_influence ()
#obtain Cook's distance for each observation
cooks = influence. cooks_distance
#display Cook's distances
print (cooks)
(array([0.368, 0.061, 0.001, 0.028, 0.105, 0.022, 0.017, 0. , 0.343,
0. , 0.15 , 0.349]),
array([0.701, 0.941, 0.999, 0.973, 0.901, 0.979, 0.983, 1. , 0.718,
1. , 0.863, 0.713]))
デフォルトでは、 cooks_ distance()関数は、各観測値のクック距離の値の配列と、それに続く対応する p 値の配列を表示します。
例えば:
- 観測 #1 のクック距離: 0.368 (p 値: 0.701)
- 観測 #2 のクック距離: 0.061 (p 値: 0.941)
- 観測 #3 のクック距離: 0.001 (p 値: 0.999)
等々。
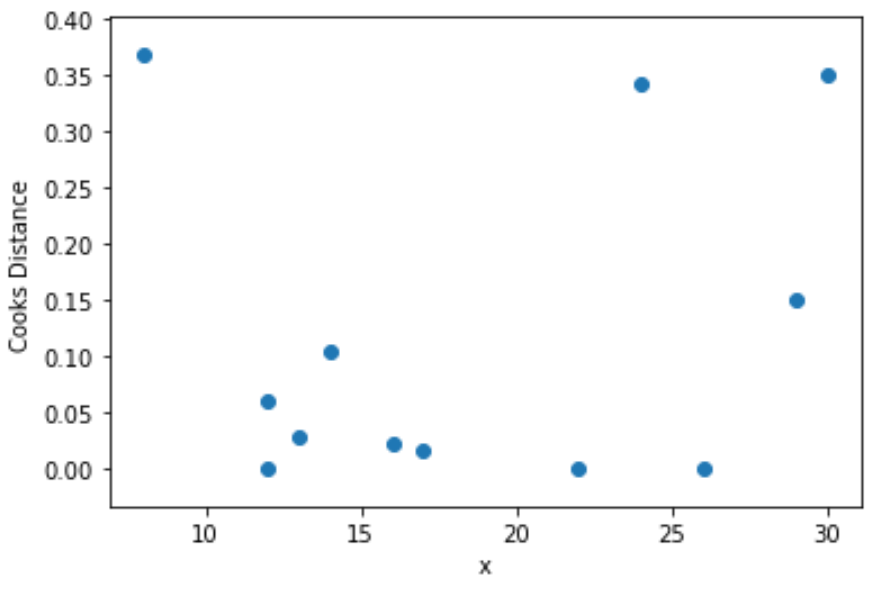
ステップ 4: 料理人の距離を視覚化する
最後に、散布図を作成して、各観測値のクック距離の関数として予測子変数の値を視覚化できます。
import matplotlib. pyplot as plt
plt. scatter (df.x, cooks[0])
plt. xlabel (' x ')
plt. ylabel (' Cooks Distance ')
plt. show ()
最終的な考え
潜在的に影響を与える観測値を特定するにはクック距離を使用する必要があることに注意することが重要です。観測値が影響力があるからといって、それをデータセットから削除する必要があるというわけではありません。
まず、観測結果がデータ入力エラーやその他の奇妙なイベントの結果ではないことを確認する必要があります。それが正当な値であることが判明した場合は、その値を削除するか、そのままにしておくか、あるいは単に中央値などの代替値に置き換えるのが適切であるかを判断できます。