グループ化されたデータの分散を求める方法 (例付き)
グループ化された度数分布の分散を計算したい場合がよくあります。
たとえば、次のようなグループ化された度数分布があるとします。

生データの値がわからないため、正確な分散を計算することはできませんが、次の式を使用して分散を推定することは可能です。
分散: Σn i (m i -μ) 2 / (N-1)
金:
- n i : i番目のグループの周波数
- mi : i番目のグループの真ん中
- μ : 平均値
- N:合計サンプルサイズ
注:各グループの中点は、範囲の下限値と上限値の平均を取ることで見つけることができます。たとえば、最初のグループの中点は次のように計算されます: (1+10) / 2 = 5.5。
次の例は、この公式を実際に使用する方法を示しています。
例: グループ化されたデータの分散を計算する
次のようなグループ化されたデータがあるとします。

前述の式を使用して、このグループ化されたデータの分散を計算する方法を次に示します。
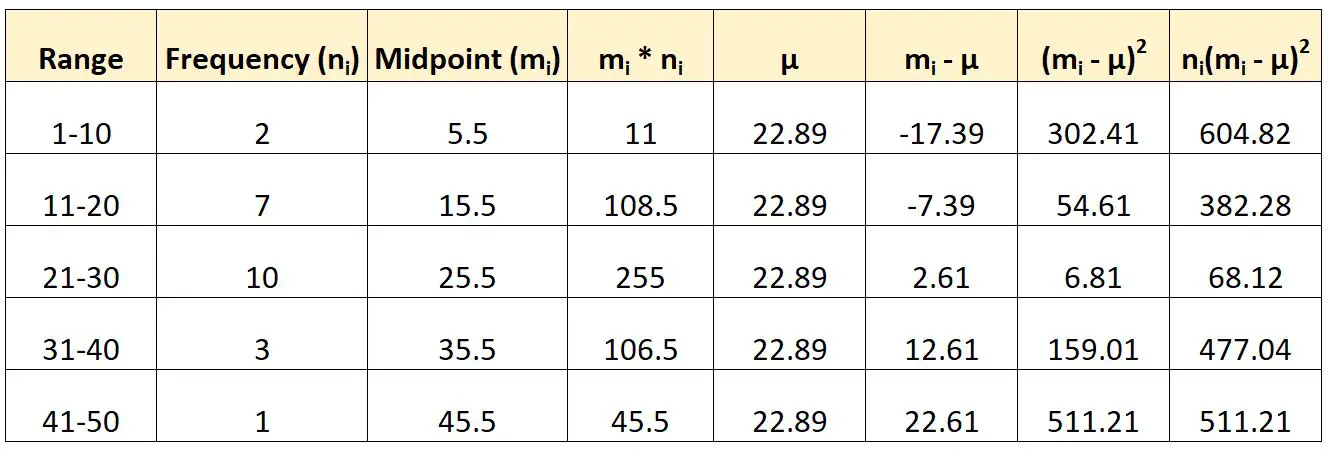
次に、次のように分散を計算します。
- 分散: Σn i (m i -μ) 2 / (N-1)
- 差: (604.82 + 382.28 + 68.12 + 477.04 + 511.21) / (23-1)
- 差: 92.885
データセットの分散は92.885であることがわかります。
追加リソース
次のチュートリアルでは、グループ化されたデータの他のメトリクスを計算する方法について説明します。
グループ化されたデータの平均と標準偏差を見つける方法
グループ化されたデータのパーセンタイル ランキングを計算する方法
グループ化されたデータの中央値を見つける方法
グループ化されたデータモードを見つける方法