Anova におけるグループ内またはグループ間の変動
一元配置分散分析は、 3 つ以上の独立したグループの平均が等しいかどうかを判断するために使用されます。
一元配置分散分析では、次の帰無仮説と対立仮説が使用されます。
- H 0 :すべてのグループ平均が等しい。
- H A :少なくとも 1 つのグループの平均が他のグループの平均とは異なります。
一元配置分散分析を実行するたびに、次のような要約表が作成されます。
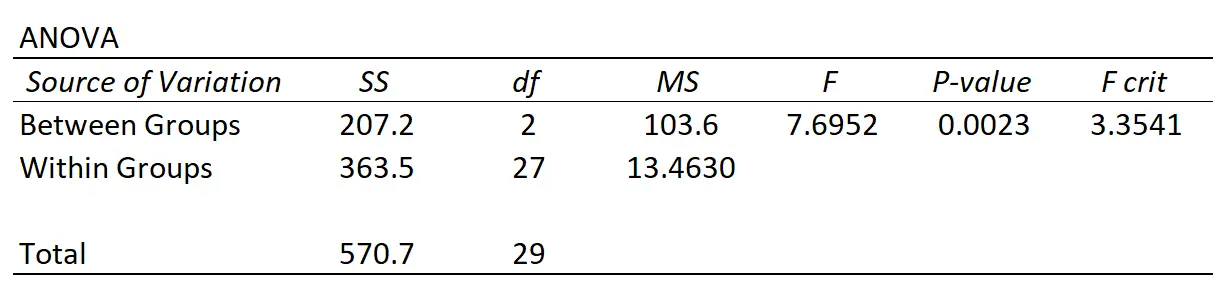
ANOVA で測定される変動には 2 つの異なるソースがあることがわかります。
グループ間の変動: 各グループの平均と全体の平均の間の合計変動。
グループ内変動:各グループの個人値の変動の合計とそのグループ平均。
グループ間の変動がグループ内の変動に比べて大きい場合、ANOVA の F 統計量はより大きくなり、対応する p 値はより低くなり、帰無仮説が棄却される可能性が高くなります。グループ平均は等しい。
次の例は、一元配置分散分析のグループ間変動とグループ内変動を実際に計算する方法を示しています。
例: ANOVA でのグループ内およびグループ間のばらつきの計算
3 つの異なる勉強法が試験の平均点の違いにつながるかどうかを判断したいとします。これをテストするために、30 人の学生を募集し、 ランダムに 10 人ずつを別の学習方法に割り当てます。
各グループの学生の試験結果は以下のとおりです。
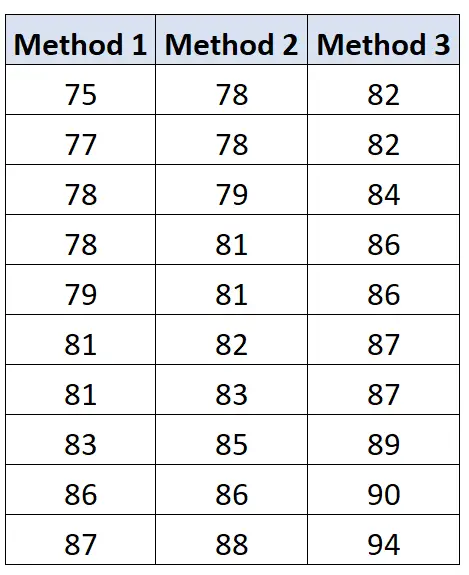
次の式を使用して、グループ間の変動を計算できます。
グループ間の変動= Σn j (X j – X ..) 2
金:
- n j : グループ j のサンプル サイズ
- Σ : 「和」を意味する記号
- X j : グループ j の平均
- X .. : 全体の平均
この値を計算するには、まず各グループの平均と全体の平均を計算します。
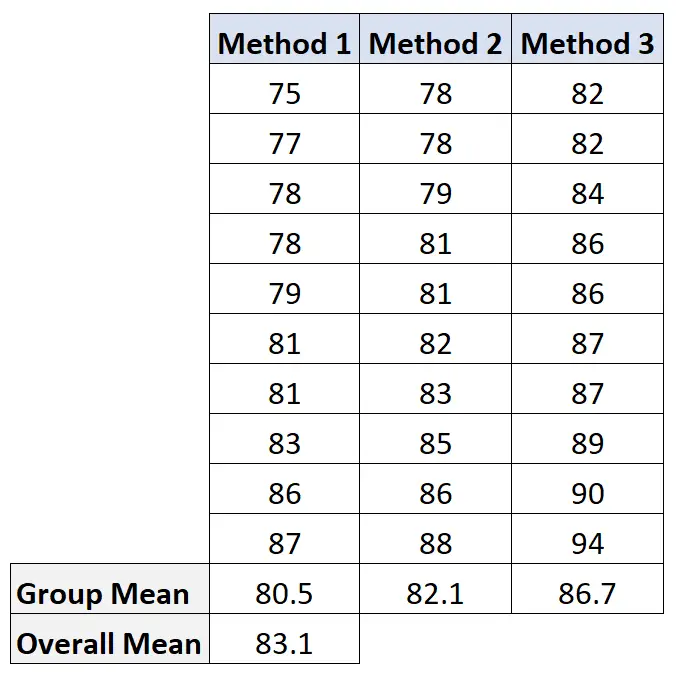
次に、グループ間の変動を次のように計算します: 10(80.5-83.1) 2 + 10(82.1-83.1) 2 + 10(86.7-83.1) 2 = 207.2 。
次に、次の式を使用してグループ内変動を計算できます。
群内変動: Σ(X ij – X j ) 2
金:
- Σ : 「和」を意味する記号
- X ij : グループ j のi 番目の観測値
- X j : グループ j の平均
この例では、グループ内の変動を次のように計算します。
グループ 1: (75-80.5) 2 + (77-80.5) 2 + (78-80.5) 2 + (78-80.5) 2 + (79-80.5) 2 + (81-80.5) 2 + (81-80.5) 2 + (83-80.5) 2 + (86-80.5) 2 + (87-80.5) 2 = 136.5
グループ 2: (78-82.1) 2 + (78-82.1) 2 + (79-82.1) 2 + (81-82.1) 2 + (81-82.1) 2 + (82-82.1) 2 + (83-82.1) 2 + (85-82.1) 2 + (86-82.1) 2 + (88-82.1) 2 = 104.9
グループ 3: (82-86.7) 2 + (82-86.7) 2 + (84-86.7) 2 + (86-86.7) 2 + (86-86.7) 2 + (87-86.7) 2 + (87-86.7) 2 + (89-86.7) 2 + (90-86.7) 2 + (94-86.7) 2 = 122.1
グループ内の変動: 136.5 + 104.9 + 122.1 = 363.5
統計ソフトウェアを使用して、このデータセットを使用して一元配置分散分析を実行すると、次の分散分析テーブルが得られます。
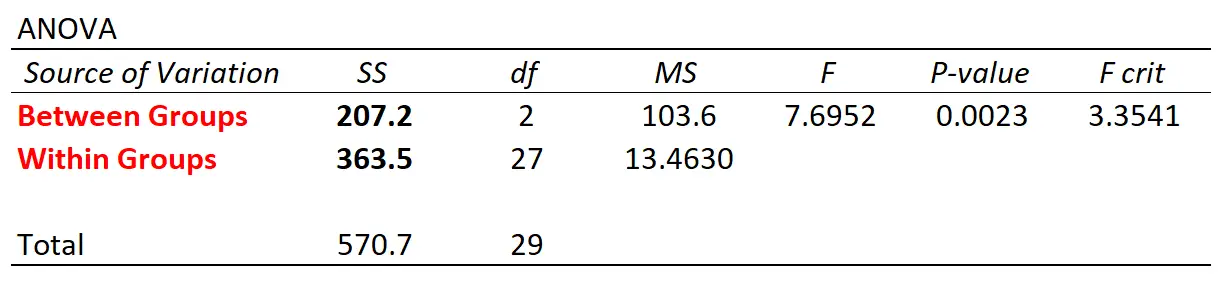
グループ間およびグループ内の変動値は、手動で計算した値と一致することに注意してください。
表の全体的な F 統計は、グループ間の変動とグループ内の変動の間の関係を定量化する方法です。
F 統計量が大きいほど、グループ内の変動と比較してグループ間の変動が大きくなります。
したがって、F 統計量が大きいほど、グループ平均間に差があることがより明確になります。
この例では、F 統計量 7.6952 に対応する p 値が.0023であることがわかります。
この値は α = 0.05 より小さいため、ANOVA の帰無仮説を棄却し、3 つの学習手法では試験で同じ得点が得られないと結論付けます。
追加リソース
次のチュートリアルでは、ANOVA モデルに関する追加情報を提供します。