Stata でクラスカル-ウォリス検定を実行する方法
クラスカル・ウォリス検定は、 3 つ以上の独立したグループの中央値間に統計的に有意な差があるかどうかを判断するために使用されます。これは、 一元配置 ANOVAと同等のノンパラメトリックとみなされます。
このチュートリアルでは、Stata でクラスカル-ウォリス テストを実行する方法を説明します。
Stata でクラスカル-ウォリス検定を実行する方法
この例では、米国の 50 州すべての 1980 年の国勢調査データを含む国勢調査データセットを使用します。データセットでは、州は 4 つの異なる地域に分類されています。
- ノルド エスト
- ノースセントラル
- 南
- 西
クラスカル-ウォリス検定を実行して、これら 4 つの地域で年齢の中央値が等しいかどうかを判断します。
ステップ 1: データをロードして表示します。
まず、コマンド ボックスに次のコマンドを入力してデータセットを読み込みます。
https://www.stata-press.com/data/r13/census を使用してください
次のコマンドを使用して、データセットの簡単な概要を取得します。
要約する
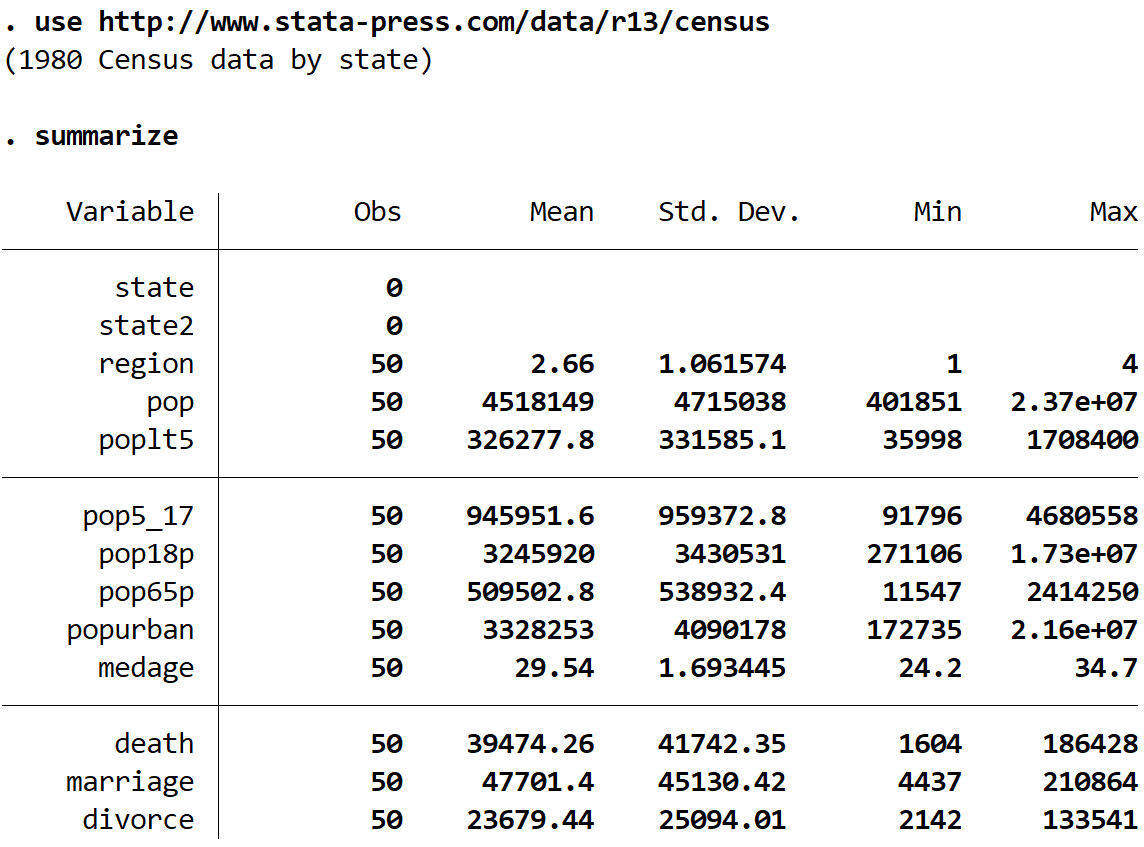
このデータセットには 13 の異なる変数があることがわかりますが、扱うのはmedage (年齢の中央値) とareaの 2 つだけです。
ステップ 2: データを視覚化します。
クラスカル-ウォリス検定を実行する前に、まずいくつかの箱ひげ図を作成して、4 つの地域それぞれの年齢分布の中央値を視覚化しましょう。
メディア グラフィック ボックス、オン (領域)
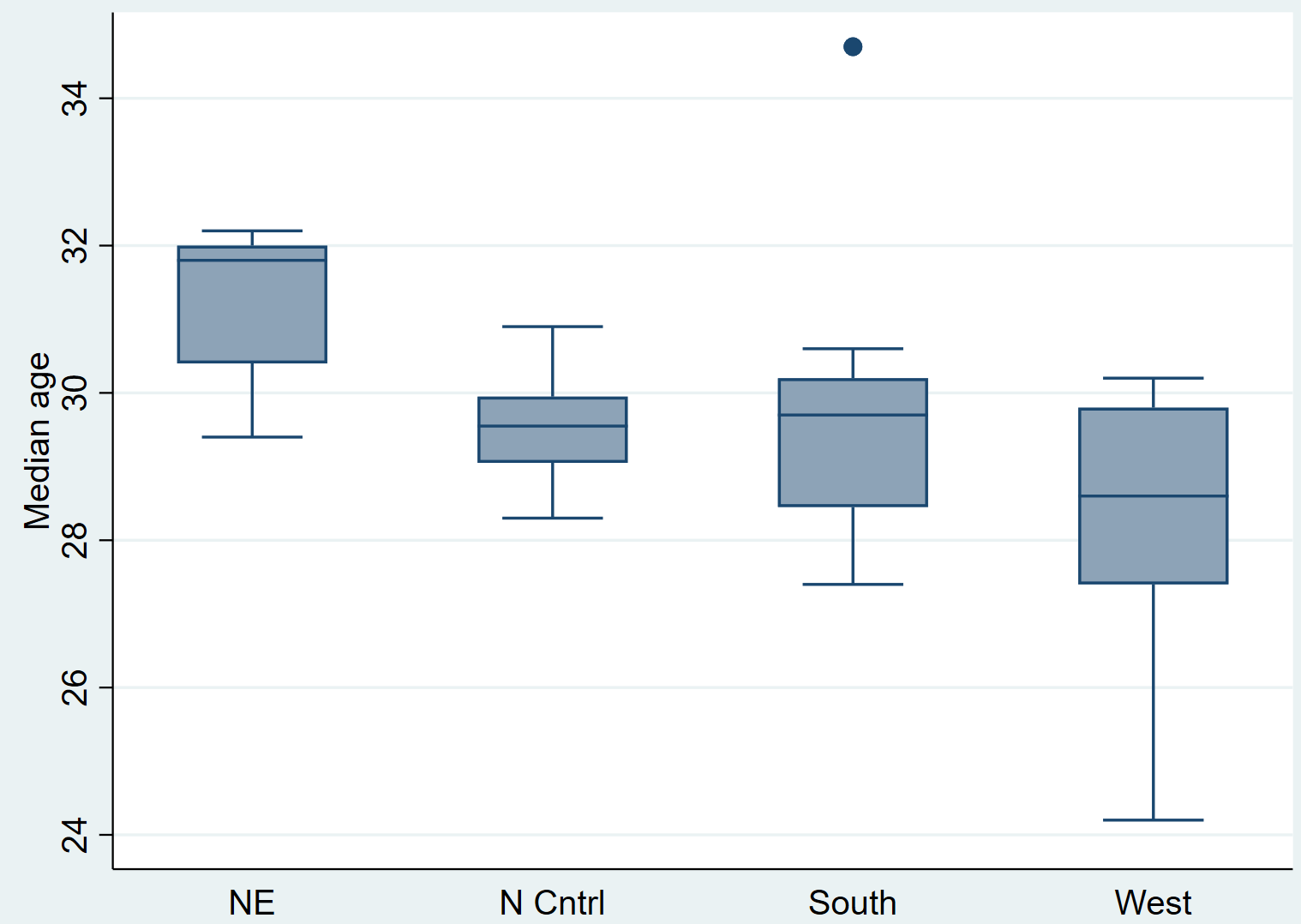
箱ひげ図を見るだけで、分布が地域ごとに異なることがわかります。次に、クラスカル-ウォリス検定を実行して、これらの違いが統計的に有意かどうかを確認します。
ステップ 3: クラスカル・ウォリス検定を実行します。
クラスカル-ウォリス検定を実行するには、次の構文を使用します。
kwallis 測定変数、(グループ化変数) による
この例では、次の構文を使用します。
クワリス・メダージュ、(地域別)
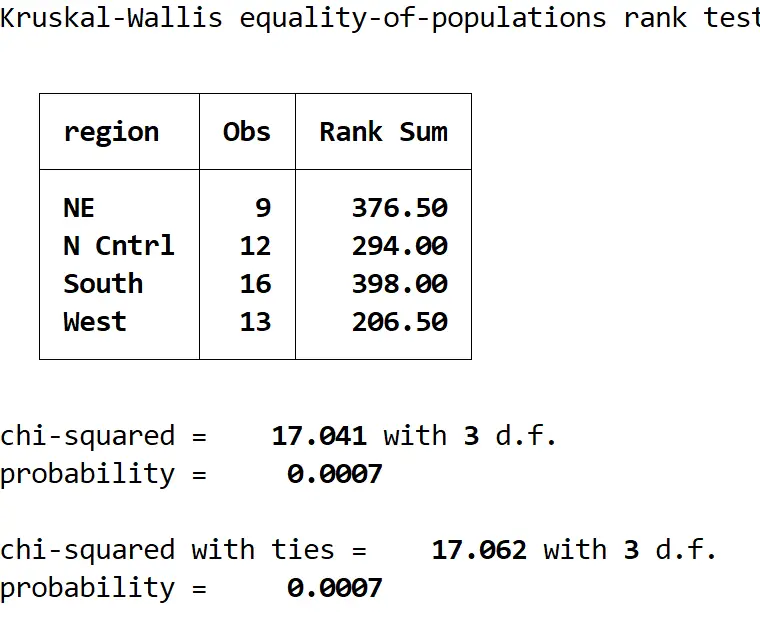
結果を解釈する方法は次のとおりです。
概要テーブル:このテーブルには、領域ごとの観測数と各領域のランキングの合計が表示されます。
タイ付きカイ二乗:これは検定統計量の値であり、17.062 であることがわかります。
確率:これは検定統計量に対応する p 値であり、0.0007 であることがわかります。この値は 0.05 未満であるため、帰無仮説を棄却し、年齢の中央値が 4 つの領域で等しくないと結論付けることができます。
ステップ 4: 結果を報告します。
最後に、クラスカル・ウォリス検定の結果を報告したいと思います。これを行う方法の例を次に示します。
米国の次の 4 つの地域で個人の年齢中央値が同じかどうかを判断するために、クラスカル-ウォリスト検定が実行されました。
- 北東 (n=9)
- 北中部 (n=12)
- 南 (n=16)
- 西 (n=13)
このテストにより、個人の年齢中央値が 4 つの地域で同じではないことが明らかになりました (X 2 = 17.062、p = 0.0007)。つまり、2 つ以上の地域間で年齢中央値に統計的に有意な差があったということです。