クラス内相関係数: 定義 + 例
クラス内相関係数(ICC) は、2 人以上の評価者がいる研究のスコアの信頼性を測定するために使用されます。
ICC の値は 0 から 1 の範囲で、0 は評価者間で信頼性がないことを示し、1 は評価者間で完全な信頼性を示します。
簡単に言うと、ICC は、項目 (またはトピック) をさまざまな評価者が確実に評価できるかどうかを判断するために使用されます。
次の 3 つの要素に応じて、計算できる ICC にはいくつかの異なるバージョンがあります。
- モデル:一方向ランダム効果、双方向ランダム効果、または双方向混合効果
- 関係のタイプ:一貫性または完全な合意
- 単位:単一の評価者または評価者の平均
以下に 3 つの異なるモデルについて簡単に説明します。
1. 一元ランダム効果モデル:このモデルは、各被験者がランダムに選択された評価者の異なるグループによって評価されることを前提としています。このモデルでは、評価者が変量効果の発生源であると考えられます。通常、各被験者の評価には同じ評価者のグループが使用されるため、このモデルが実際に使用されることはほとんどありません。
2. 二元ランダム効果モデル:このモデルは、評価者のグループkが母集団からランダムに選択され、被験者の評価に使用されると仮定します。このモデルを使用すると、評価者と被験者は変量効果の発生源とみなされます。このモデルは、研究で使用された評価者と同様の評価者に結果を一般化したい場合によく使用されます。
3. 二元混合効果モデル:このモデルはまた、評価者のグループkが母集団からランダムに選択され、被験者の評価に使用されることを前提としています。ただし、このモデルは、私たちが選択した評価者のグループが関心のある唯一の評価者であることを前提としています。これは、研究で使用された評価者と同様の特性を共有する可能性のある他の評価者に結果を一般化したくないことを意味します。
ここでは、測定したい 2 つの異なるタイプの関係について簡単に説明します。
1. 一貫性:審査員の評価間の体系的な違いに興味があります (たとえば、審査員は同様のトピックを低いと評価しましたか?)。
2. 絶対一致:ジャッジのスコア間の絶対的な差に興味があります (たとえば、ジャッジ A とジャッジ B のスコアの絶対的な差は何ですか?)。
ここでは、興味深い 2 つの異なるユニットについて簡単に説明します。
1. 単一のレビュー担当者:測定の基準として 1 人のレビュー担当者の評価のみを使用したいと考えています。
2. 評価者の平均:すべての審査員のスコアの平均を測定の基準として使用したいと考えています。
注:二分法結果に関する各項目を見逃した 2 人の評価者の間の一致レベルを測定したい場合は、代わりにCohen の Kappaを使用する必要があります。
クラス内相関係数の解釈方法
Koo と Liによると、クラス内相関係数の値を解釈する方法は次のとおりです。
- 0.50未満:信頼性が低い
- 0.5 ~ 0.75: 中程度の信頼性
- 0.75 ~ 0.9:良好な信頼性
- 0.9以上:優れた信頼性
次の例は、実際にクラス内相関係数を計算する方法を示しています。
例:クラス内相関係数の計算
4 人の異なる裁判官が 10 の異なる大学入学試験の質を評価するように依頼されたとします。結果を以下に示します。
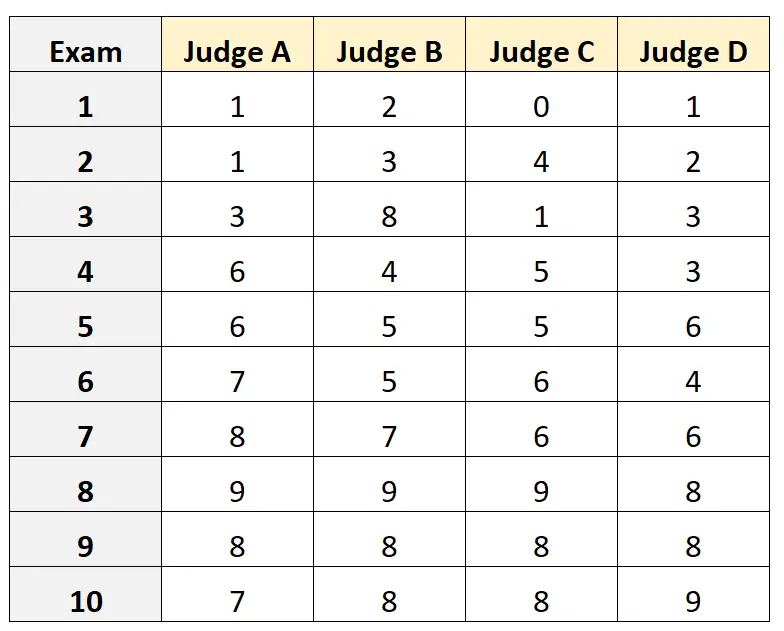
入学試験の資格のある審査員の母集団から 4 人の審査員がランダムに選ばれ、審査員間の絶対的な一致度を測定し、測定の基礎として 1 人の評価者の観点からのスコアを使用したいとします。
R で次のコードを使用すると、評価者間の関係として絶対的な一致を使用し、対象の単位として単一の単位を使用して、双方向変量効果モデルを近似できます。
#load the interrater reliability package library (irr) #define data data <- data. frame (A=c(1, 1, 3, 6, 6, 7, 8, 9, 8, 7), B=c(2, 3, 8, 4, 5, 5, 7, 9, 8, 8), C=c(0, 4, 1, 5, 5, 6, 6, 9, 8, 8), D=c(1, 2, 3, 3, 6, 4, 6, 8, 8, 9)) #calculate ICC icc(data, model = " twoway ", type = " agreement ", unit = " single ") Model: twoway Type: agreement Subjects = 10 Failures = 4 ICC(A,1) = 0.782 F-Test, H0: r0 = 0; H1: r0 > 0 F(9.30) = 15.3, p = 5.93e-09 95%-Confidence Interval for ICC Population Values: 0.554 < ICC < 0.931
クラス内相関係数 (ICC) は0.782であることがわかりました。
ICC を解釈するための経験則に基づいて、ICC 0.782は、さまざまな評価者によって試験が「良好な」信頼性で採点できることを示していると結論付けます。
追加リソース
次のチュートリアルでは、さまざまな統計ソフトウェアで ICC を計算する方法について詳しく説明します。
Excel でクラス内相関係数を計算する方法
Rでクラス内相関係数を計算する方法
Python でクラス内相関係数を計算する方法