クリティカル値
この記事では、統計における臨界値とは何か、また仮説検定においてそれをどのように解釈すべきかについて説明します。同様に、クリティカル値の計算方法といくつかの具体例を確認できます。
クリティカル値とは何ですか?
臨界値は、帰無仮説の棄却領域と許容領域を分ける検定統計量の分布内の点です。言い換えれば、臨界値は、棄却領域 (または臨界領域) の限界をマークする統計検定の分布の値です。
通常、最も一般的な参照分布は標準正規分布であるため、臨界値は記号 Z α/2で表されます。
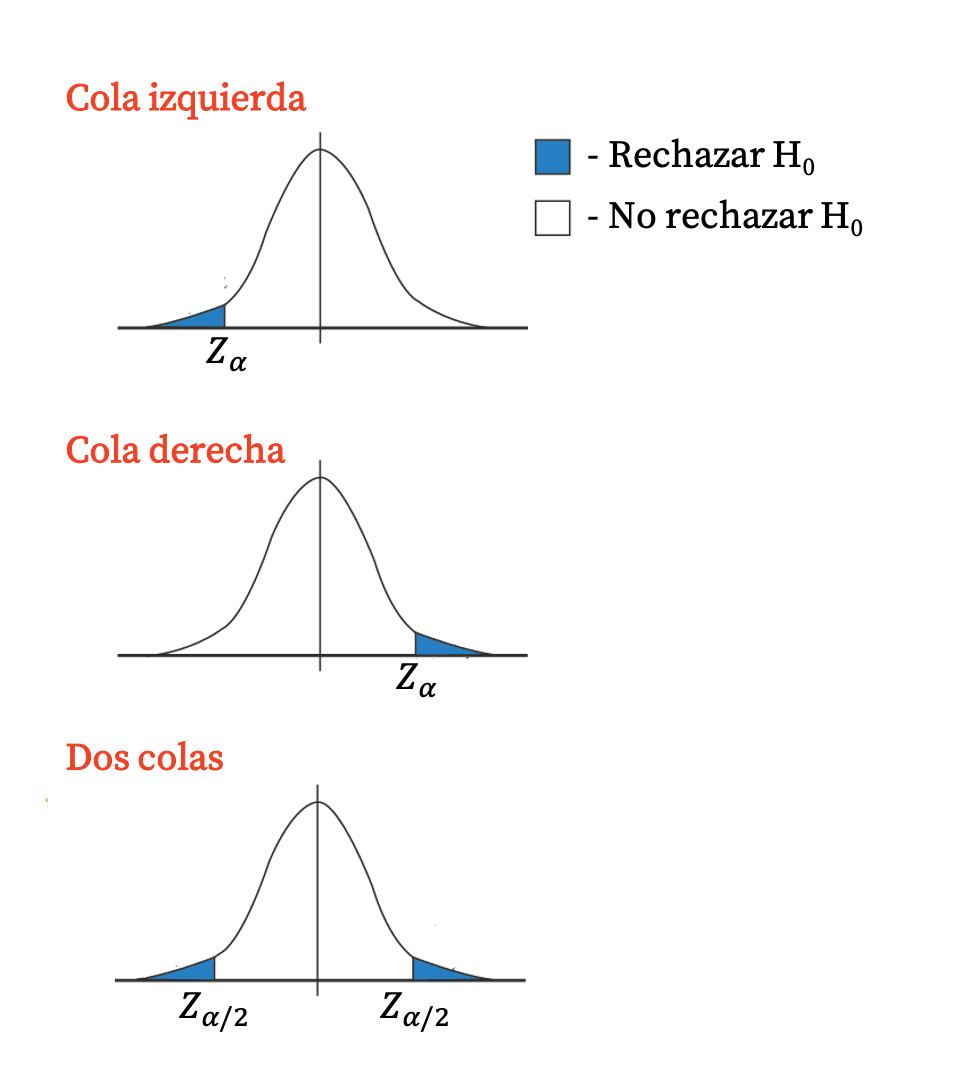
一般に、棄却領域は分布の単一の裾を構成するため、片側検定は非常に重要です。一方、両側検定には、棄却領域が分布の両方の裾に対応するため、2 つの臨界値があります。
信頼区間では、臨界値は、信頼区間の限界を示す参照分布内の点です。
クリティカル値の計算方法
次に、最も一般的な臨界値がどのように計算されるかを見ていきます。 Z の臨界値と t の臨界値は平均の信頼区間に対して計算されます。唯一の違いは、Z の臨界値は母標準偏差が既知の場合に計算され、代わりに t の臨界値が使用されることです。 1 つのサンプルのデータしかわかっていない場合。
Zの臨界値
Z の臨界値は、平均の信頼区間の限界を決定するために使用されます。より正確には、母集団の標準偏差がわかっている場合にのみ使用されます。
Z の臨界値を計算するには、有意水準の半分の確率に対応する値を標準正規分布表で見つける必要があります。
たとえば、信頼水準 95% で平均の信頼区間を決定したい場合、これは有意水準が 5% であることを意味します。したがって、平均値の信頼区間は両側であるため、標準正規分布の表でどの値が 2.5% の確率に対応するかを確認する必要があります。
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-54dda39d0da5b29f2d25728b89565859_l3.png)
以下に、最も使用される重要な Z 値の表を示します。
| 信頼水準 (1-α) | 有意水準(α) | クリティカル値(Z α/2 ) |
|---|---|---|
| 0.80 | 0.20 | 1,282 |
| 0.85 | 0.15 | 1,440 |
| 0.90 | 0.10 | 1,645 |
| 0.95 | 0.05 | 1960年 |
| 0.99 | 0.01 | 2,576 |
| 0.995 | 0.005 | 2,807 |
| 0.999 | 0.001 | 3,291 |
tの臨界値
臨界 t 値は、母集団の標準偏差が不明な場合に、平均の信頼区間の限界を見つけるために使用されます。
t の臨界値を計算するには、スチューデントの t 分布の自由度が単位であることを考慮して、有意水準の半分の確率に対応する値をスチューデントの t 分布テーブルで見つける必要があります。サンプルサイズよりも。
たとえば、信頼水準 95% でサンプル サイズが 8 の信頼区間を見つけたい場合、スチューデントの t 分布表にアクセスして、どの値が t 0.025|7に対応するかを確認する必要があります。
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}t_{\alpha/2| n-1}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 7}=2,365\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-2caa8c4576ebc261acfdb1341dc4567d_l3.png)
仮説検証における重要な価値
臨界値は、仮説検定で帰無仮説を棄却する (対立仮説を受け入れる) か、対立仮説を棄却する (帰無仮説を受け入れる) ために使用することもできます。
- p 値に対応する検定統計量の分布の値が臨界値でマークされた区間内にある場合、帰無仮説は棄却されません (対立仮説は棄却されます)。
- p 値に対応する検定統計量の分布の値が臨界値でマークされた区間外にある場合、帰無仮説は棄却されます (対立仮説は受け入れられます)。