ケンダルのタウ: 定義 + 例
統計学において、相関とは、2 つの変数間の関係の強さと方向を指します。相関係数の値の範囲は -1 ~ 1 で、-1 は完全な負の関係を示し、0 は関係がないことを示し、1 は完全な正の関係を示します。
最も一般的に使用される相関係数は、2 つの数値変数間の線形関連を測定する ピアソン相関係数です。
あまり一般的には使用されない相関係数は、ランク付けされたデータの 2 つの列間の関係を測定するKendall のタウです。
ケンダルのタウ (しばしば τ と略される) を計算する式は次のとおりです。
τ = (CD) / (C+D)
金:
C = 一致するペアの数
D = 不一致のペアの数
次の例は、この式を使用して、ランク付けされたデータの 2 つの列のケンドールのタウ順位相関係数を計算する方法を示しています。
ケンダルのタウの計算例
2 人のバスケットボール コーチが選手 12 人を最悪から最高までランク付けすると仮定します。次の表は、各コーチが選手に割り当てたランキングを示しています。
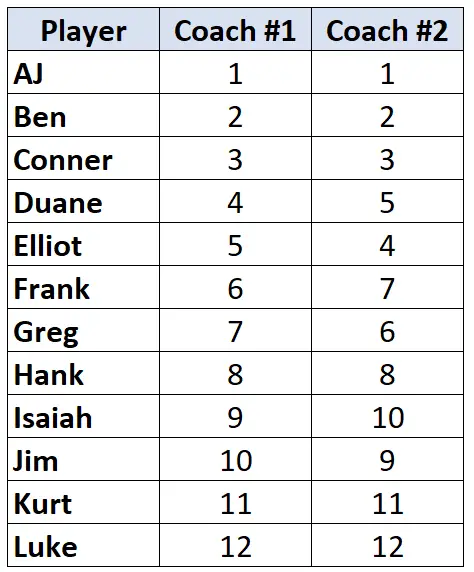
ランク付けされたデータの 2 つの列を使用しているため、ケンダルのタウを使用して 2 人のコーチのランキング間の相関関係を計算するのが適切です。ケンダルのタウを計算するには、次の手順に従います。
ステップ 1: 一致するペアの数を数えます。
コーチ #2 のランキングだけを見てください。最初のプレイヤーから始めて、そのプレイヤーより何ランク下の人が背が高いかを数えます。たとえば、「1」の下には大きい数字が 11 個あるので、11 と書きます。
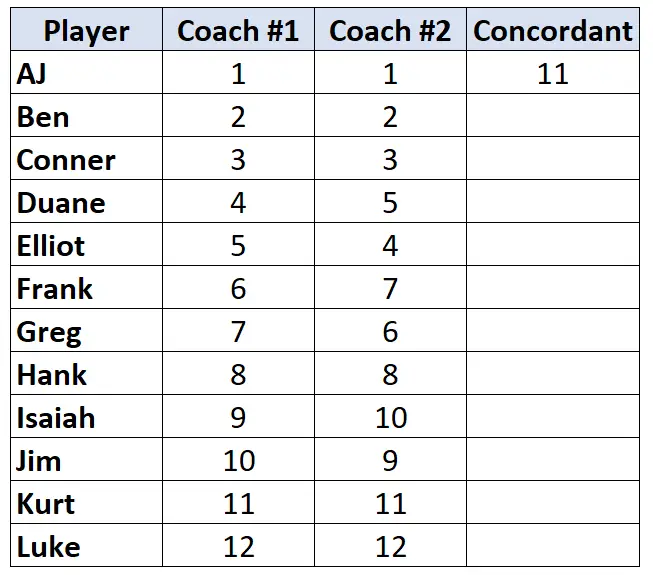
次のプレーヤーに移動し、このプロセスを繰り返します。 「2」の下に大きい数字が 10 個あるので、10 を書きます。
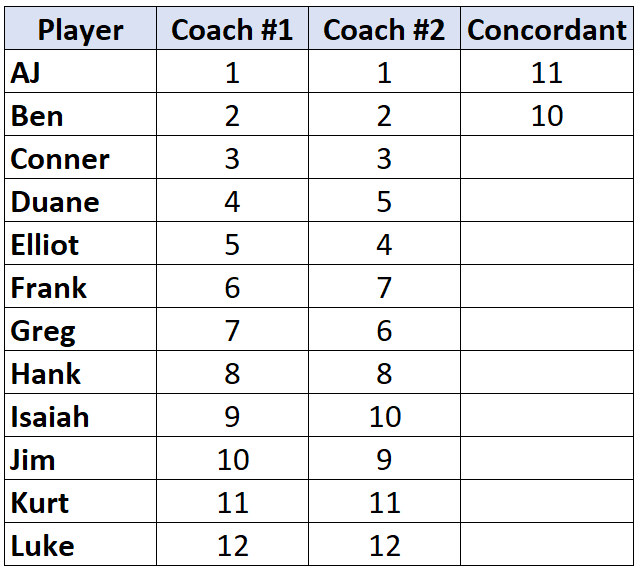
前のプレーヤーよりもランクが低いプレーヤーに到達すると、そのプレーヤーには前のプレーヤーと同じ値が割り当てられるだけです。たとえば、エリオットのランクは「4」で、前のプレイヤーのランク「5」よりも低いため、単純に前のプレイヤーと同じ値が割り当てられます。
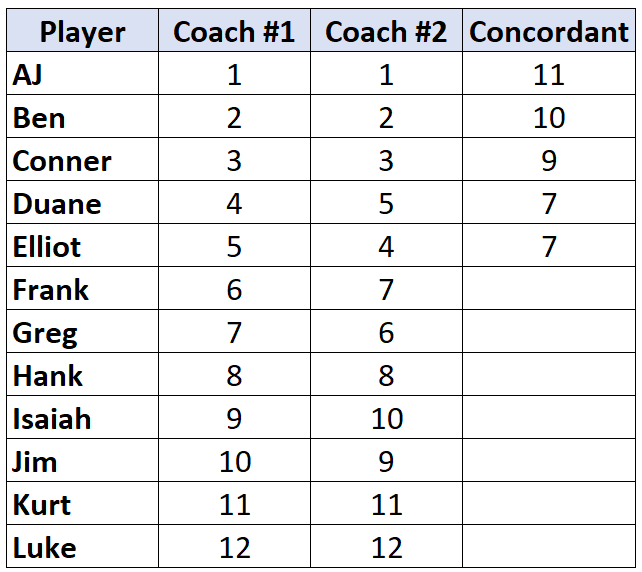
すべてのプレイヤーに対してこのプロセスを繰り返します。
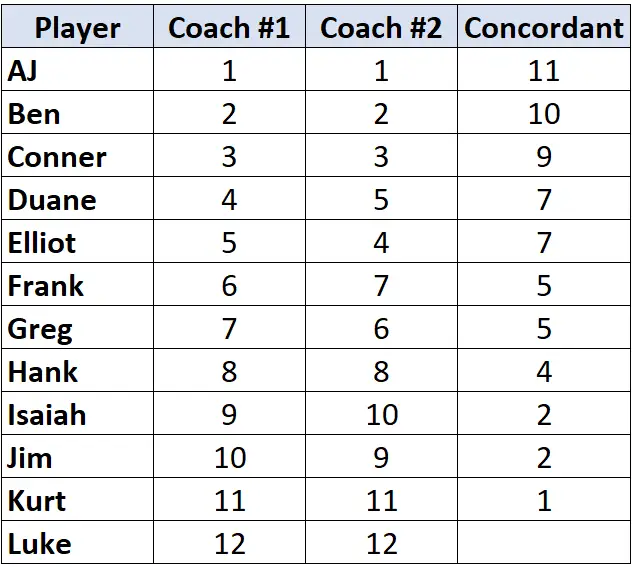
ステップ 2: 不一致のペアの数を数えます。
繰り返しになりますが、コーチ #2 のランキングだけを見てください。各プレイヤーについて、自分より何ランク下が小さいかを数えます。たとえば、コーチ #2 は AJ にランク「1」を割り当て、彼より下のプレーヤーはそれより低いランクを持ちません。したがって、値 0 を割り当てます。
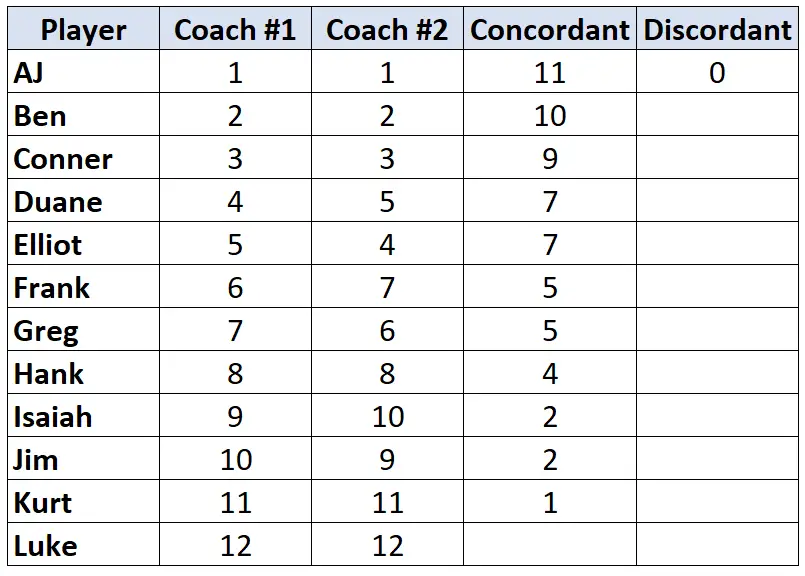
各プレーヤーに対してこのプロセスを繰り返します。
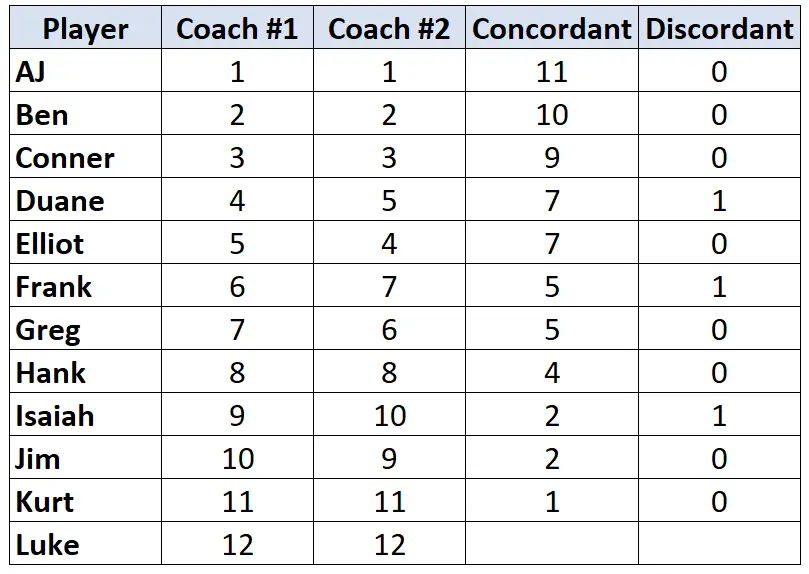
ステップ 3: 各列の合計を計算し、ケンダルのタウを求めます。
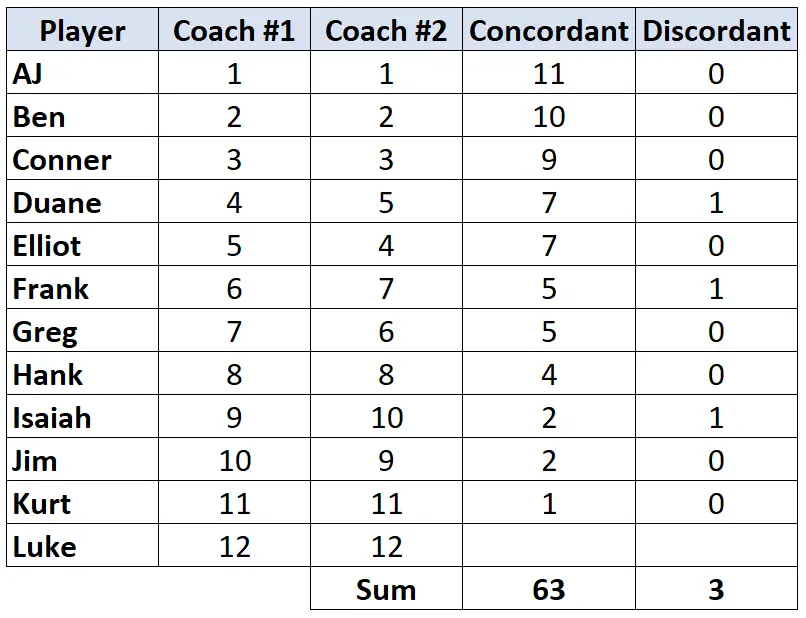
ケンダルのタウ = (CD) / (C+D) = (63-3) / (63+3) = (60/66) = 0.909 。
ケンダルタウの統計的重要性
n=10 を超えるペアがある場合、ケンダルのタウは通常正規分布に従います。次の式を使用して、ケンダルのタウの Z スコアを計算できます。
z = 3τ*√ n(n-1) / √ 2(2n+5)
金:
τ = ケンダルのタウについて計算した値
n = ペアの数
前の例のz を計算する方法は次のとおりです。
z = 3(.909)*√ 12(12-1) / √ 2(2*12+5) = 4.11 。
P 値 Z スコア計算ツールを使用すると、この Z スコアの p 値は0.00004であり、0.05 アルファ レベルで統計的に有意であることがわかります。したがって、2 人のコーチが選手に割り当てたランクの間には統計的に有意な相関関係があります。
ボーナス: R でケンダルのタウを計算する方法
R 統計ソフトウェアでは、VGAM ライブラリのkendall.tau()関数を使用して、次の構文を使用して 2 つのベクトルのケンダルのタウを計算できます。
ケンダル.タウ(x, y)
ここで、 xとyは同じ長さの 2 つのデジタル ベクトルです。
次のコードは、前の例で使用した正確なデータに対してケンダルのタウを計算する方法を示しています。
#load VGAM library(VGAM) #create vector for each coach's rankings coach_1 <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12) coach_2 <- c(1, 2, 3, 5, 4, 7, 6, 8, 10, 9, 11, 12) #calculate Kendall's Tau kendall.tau(coach_1, coach_2) #[1] 0.9090909
Kendall のタウ値が手動で計算した値とどのように一致しているかに注目してください。