コクランのqテストとは何ですか? (定義&例)
コクランの Q テストは、各グループに同じ個人が出現する 3 つ以上のグループで「成功」の割合が等しいかどうかを判断するために使用される統計テストです。
たとえば、コクランの Q テストを使用して、3 つの異なる学習手法を使用した場合にテストに合格する生徒の割合が等しいかどうかを判断できます。

コクランの Q テストを実行する手順
コクランの Q 検定では、次の帰無仮説と対立仮説が使用されます。
帰無仮説 (H 0 ): 「成功」の割合はすべてのグループで同じです
対立仮説 ( HA ): 「成功」の割合は少なくとも 1 つのグループで異なります。
検定統計量は次のように計算されます。
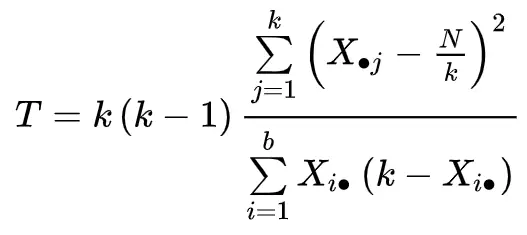
金:
- k:治療数 (または「グループ」)
- Xj: j 番目の処理の列の合計
- b:ブロック数
- シーさん。 : i 番目のブロックの行の合計
- N:総計
T検定統計量は、k-1自由度のカイ二乗分布に従います。
検定統計量に関連付けられたp 値が特定の有意レベル (α = 0.05 など) を下回っている場合、帰無仮説を棄却し、「成功」の割合が異なると言える十分な証拠があると結論付けることができます。グループのうちの少なくとも 1 つ。
例: コクランの Q テスト
研究者が、3 つの異なる学習手法が生徒間の成功率の異なる割合につながるかどうかを知りたいと考えているとします。
これをテストするために、彼女は 20 人の学生を募集し、それぞれ 3 つの異なる学習方法を使用して同じ難易度の試験を受けさせます。結果を以下に示します。

コクランの Q テストを手動で実行するのは面倒なため、統計ソフトウェアを使用できます。
このデータセットを作成し、R 統計プログラミング言語でコクランの Q テストを実行するために使用できるコードは次のとおりです。
#load DescTools package library (DescTools) #create dataset df <- data.frame(student= rep (1:20, each = 3 ), technique= rep (c('A', 'B', 'C'), times= 20 ), outcome=c(1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1)) #perform Cochran's Q test CochranQTest(outcome ~ technique| student, data=df) Cochran's Q test data: outcome and technique and student Q = 0.33333, df = 2, p-value = 0.8465
テスト結果から次のことがわかります。
- 検定統計量は0.333です
- 対応する p 値は0.8465です。
この p 値は 0.05 未満ではないため、帰無仮説を棄却できません。
これは、学生が使用する学習手法によって成功率の割合が異なると言える十分な証拠がないことを意味します。