Pコントロールカード
この記事では、P 管理図とは何か、またその用途について説明します。また、P 管理図の作成方法についても説明し、さらに、演習を段階的に解くことができます。
P管理図とは何ですか?
P 管理図、または単にP 管理図は、欠陥のあるユニットの割合とその管理限界の推移を表すグラフです。したがって、P管理図は不良品の割合を管理するために使用される管理図です。
品質管理では、生産プロセスでユニットが正しく製造されているかどうか、あるいは逆に欠陥が多すぎるかどうかを調査する必要があることがよくあります。したがって、管理図 P により、不良品の割合の推移を分析し、生産プロセスがいつ管理下にあるか、いつ管理下にあるかを確認することができます。
ただし、P 管理図は生産プロセスの管理に使用されるだけでなく、患者の割合の管理や二値実験の成功率の管理など、他の用途もあります。主に生産プロセスの制御に使用されます。
P 管理図の特徴の 1 つは、分析されるさまざまなサンプルのサイズが必ずしも等しい必要がないため、統計調査を実行するために異なるサイズのサンプルを取得できることです。
つまり、P 管理図を使用すると、「成功」(正常に生産されたユニット) と「失敗」(欠陥のあるユニット) という 2 つの結果が考えられるケースを分析できます。つまり、P 管理図は二項分布に従う場合に役立ちます。
P管理図の作成方法
P 管理図を作成するには、次の手順に従う必要があります。
- サンプルを取得する: まず、グラフ内の割合がどのように変化するかを確認するために、さまざまなサンプルを取得する必要があります。サンプルのサイズはさまざまですが、少なくとも 20 個のサンプルを採取することをお勧めします。
- 割合 p を計算する: 各サンプルについて、欠損のある個人の割合を計算する必要があります。
- 割合の平均値を計算します。調査したすべての要素から、不良ユニットの合計割合を計算する必要があります。
- P 管理図の管理限界を計算する: テストしたサンプルごとに、以下の式を使用して管理限界を見つける必要があります。各サンプルのサイズが異なる場合、管理限界の値も異なることに注意してください。
- 値をグラフにプロットする: 次に、取得したサンプル比率の値と計算された管理限界をグラフにプロットする必要があります。
- 管理図 P を分析します。最後に残っているのは、比率の値が管理限界を超えていないこと、したがってプロセスが管理下にあることを確認することだけです。そうでない場合は、生産プロセスを修正するための措置を講じる必要があります。
![]()
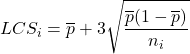
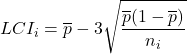
金
![]()
そして
![]()
はそれぞれサンプル i の管理限界の上限と下限であり、
![]()
は欠陥の割合の平均値であり、
![]()
はサンプルサイズ i です。
P管理図の例
概念の理解を完了するには、コントロール カード P を作成する解決済みの例を見ていきます。
- ある企業は 25 個の製品サンプルを収集し、各サンプルにサンプルのサイズと見つかった欠陥部品の数を記録しました。収集されたデータは次の表で確認できます。
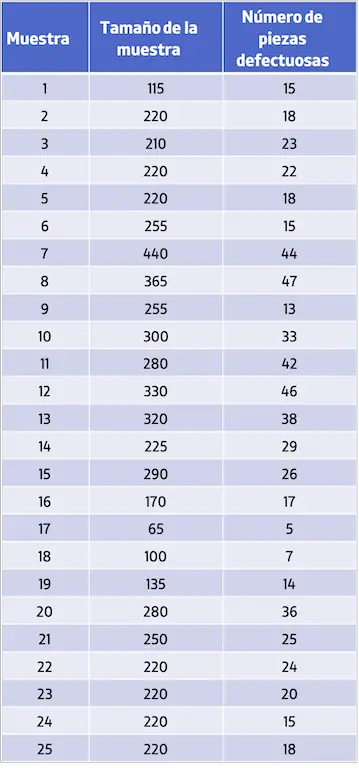
管理図Pを作成するには、まず不良品の総割合を算出する必要がある。これを行うには、欠陥の総数を生産されたユニットの総数で割るだけです。
![]()
次に、各サンプルの欠陥の割合と各サンプルの管理限界を計算しましょう。例として、最初のサンプルの計算に進みます。
![]()
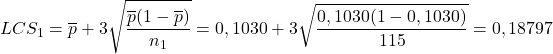
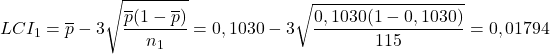
したがって、各サンプルの欠陥の割合と管理限界は次のようになります。
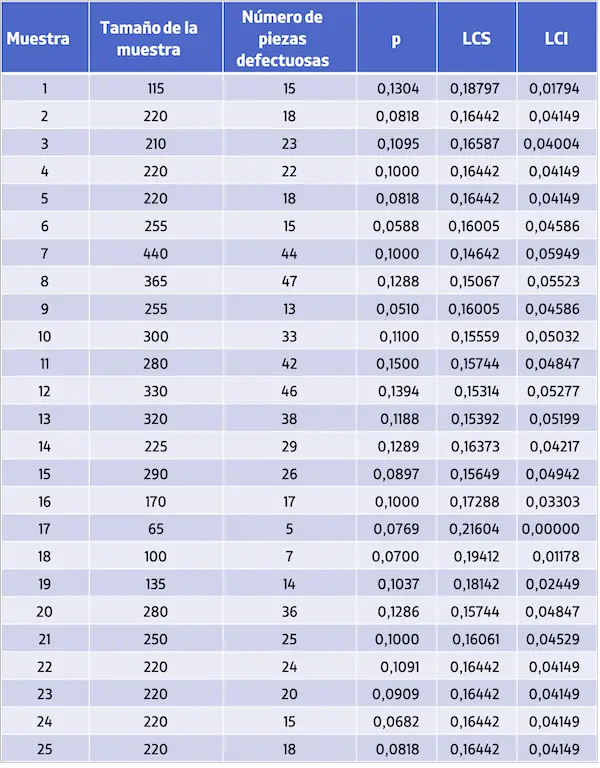
すべての管理限界を計算したら、欠陥割合とその管理限界の値をグラフ上に表して、管理グラフ P を取得します。
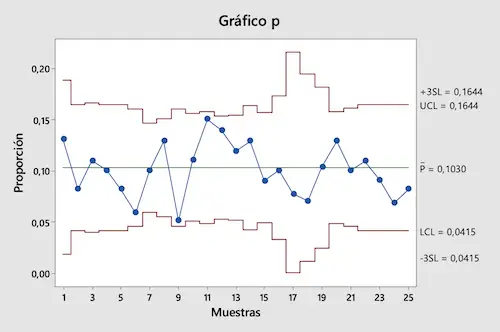
グラフからわかるように、すべての割合値は管理限界内にあります。したがって、調査した生産プロセスは管理下にあると結論付けます。
他の種類の管理図
P管理図は属性管理図の一種です。その他の既存の属性管理図には次のものがあります。
- NP 管理カード– P カードとは異なり、不良品の割合ではなく、不良品の数が管理されます。
- コントロールカードC : 障害の発生数を監視します。
- 管理チャート U : 欠陥の数はチャート C と同様に管理されますが、サンプル サイズは可変です。