ダービン・ワトソン検定: 定義と例
線形回帰の主な前提の 1 つは、連続する残差間に相関関係がないということです。言い換えれば、残差は独立していると仮定します。
この仮定に違反すると、回帰モデルの係数の標準誤差が過小評価される可能性が高くなります。つまり、予測変数が統計的に有意ではない場合でも、統計的に有意であるとみなされる可能性が高くなります。現実には存在しません。
この仮定が満たされているかどうかを判断する 1 つの方法は、ダービン・ワトソン検定を実行することです。これは、回帰の残差における自己相関の存在を検出するために使用されます。
ダービン-ワトソンテストを実行する手順
ダービン-ワトソン検定では次の仮定が使用されます。
H 0 (帰無仮説):残差間に相関はありません。
H A (対立仮説):残差は自己相関します。
ダービン-ワトソン検定の検定統計量 (通常はdで表されます) は次のように計算されます。
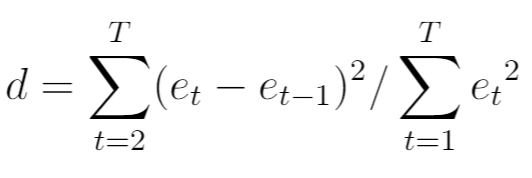
金:
- T:観測値の総数
- e t :回帰モデルの t番目の残差
検定統計量の範囲は常に 0 ~ 4 です。
- d = 2 は自己相関がないことを示します
- d < 2 は正の系列相関を示します
- d > 2 は負の系列相関を示します
一般に、 dが 1.5 未満または 2.5 を超える場合、重大な自己相関問題が発生する可能性があります。それ以外の場合、 d が1.5 ~ 2.5 の間であれば、自己相関はおそらく問題になりません。
ダービン-ワトソン検定統計量が特定のアルファ レベルで有意であるかどうかを判断するには、この臨界値の表を参照できます。
ダービン-ワトソン検定統計量の絶対値が表にある値より大きい場合、検定の帰無仮説を棄却し、自己相関が存在すると結論付けることができます。
自己相関が検出された場合の対処方法
ダービン-ワトソン検定の帰無仮説を棄却し、残差に自己相関が存在すると結論付けた場合、問題が十分に深刻であると考えられる場合、この問題を修正するためのいくつかの異なるオプションがあります。
- 正の系列相関を得るには、従属変数および/または独立変数のラグをモデルに追加することを検討してください。
- 負のシリアル相関の場合は、どの変数も遅延しすぎていないことを確認してください。
- 季節相関については、モデルに季節ダミーを追加することを検討してください。
通常、これらの戦略は自己相関問題を解決するのに十分です。
ダービン・ワトソン検定の実行例
ダービン ワトソン テストの段階的な例については、さまざまな統計ソフトウェアを使用してテストを実行する方法を説明する次のチュートリアルを参照してください。
R でダービン・ワトソンテストを実行する方法
Python でダービン-ワトソン テストを実行する方法
Excel でダービン-ワトソン テストを実行する方法