チェビシェフの定理

この記事ではチェビシェフの定理とは何かについて説明します。ここでは、チェビシェフの定理の公式、解答済みの練習問題、さらにオンラインのチェビシェフの定理計算ツールを見つけることができます。最後に、チェビシェフの定理と経験則の違いを示します。

チェビシェフの定理とは何ですか?

チェビシェフの定理 は、チェビシェフの不等式としても知られ、確率変数の値が平均から一定の距離内にある確率を計算するために使用される統計規則です。

言い換えれば、統計学では、値が信頼区間内にある確率を決定するためにチェビシェフの定理が使用されます。

さらに、チェビシェフの定理は、大数の法則などの他の統計定理を証明するためにも使用されます。

チェビシェフの定理はフランス人のイレネー＝ジュール・ビネメによって最初に定式化されましたが、この定理は 1867 年にロシアのパフヌティ・チェブシェフによって考案されたため、このように名付けられました。

チェビシェフの定理の公式

チェビシェフの定理は、値が平均からk 標準偏差に等しい確率は、1 から 1 をkの 2 乗で割った比率を引いた値以上であると述べています。

したがって、チェビシェフの定理の公式は次のようになります。

金

は確率変数の値です。

変数の算術平均、

その標準偏差と

確率が計算される平均からの標準偏差の数。

この式は、計算が実行される標準偏差の数が 1 より大きい場合、つまりkが 1 より大きい場合にのみ使用できることに注意してください。

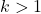以下のオンラインのチェビシェフの定理計算ツールを使用して確率を計算できます。

チェビシェフの定理の例

チェビシェフの定理の定義とその公式が何であるかを理解したら、概念をよりよく理解するためにこの統計定理の解決例を示します。

• 大学のコース統計で獲得した成績が平均 65、標準偏差 10 の分布で定義されている場合、50 ～ 80 の成績を獲得した学生の割合は何パーセントでしょうか?

この問題を解決するには、チェビシェフの定理の公式を適用する必要があります。ただし、値 50 と 80 が変数の平均からどれだけの標準偏差があるかを最初に決定する必要があります。これを行うには、次の計算を行うだけです。

したがって、値 50 と 80 は、それぞれ下位平均と上位平均からの 1.5 標準偏差に対応します。したがって、k=1.5 のチェビシェバの定理の式を使用します。

したがって、少なくとも 55.56% の学生が 50 から 80 の間の成績を獲得しました。

チェビシェフの定理計算機

問題の値と平均値の間の標準偏差の数(k)を入力し、「計算」をクリックします。計算機は信頼区間の最小確率を返します。

標準偏差の数は、小数点区切り文字としてドットを使用して入力する必要があります。

チェビシェフの定理と経験則

統計学における 2 つの密接に関連した概念は、チェビシェフの定理と経験則です。どちらも信頼区間の確率を計算するために使用されます。

チェビシェフの定理と経験則の違いは、チェビシェフの定理はあらゆるタイプの分布に使用できるのに対し、経験則は正規分布にのみ有効であることです。

したがって、チェビシェフの定理の使用範囲は広くなりますが、経験則の方が正規分布に対してより正確な結果が得られます。

経験則が何であるかを正確に確認するには、ここをクリックしてください。