Excel でチェビシェフの定理を適用する方法

チェビシェフの定理は、1 より大きい任意の数値 k について、学習済み分布内のデータ値の少なくとも1 – 1/k ²が平均から k 標準偏差以内にあることを示しています。

たとえば、どのような形状の分布でも、分布内の値の少なくとも 1 – 1/3 ² = 88.89% が平均の 3 標準偏差以内に収まります。

このチュートリアルでは、Excel でチェビシェフの定理を適用するいくつかの例を示します。

例 1: チェビシェフの定理を使用して、平均が 50、標準偏差が 10 のデータセットについて、値の何パーセントが 30 ～ 70 の間に収まるかを決定します。

まず、k の値を決定します。これは、平均から 30 ～ 70 の間に標準偏差がいくつあるかを決定することで実行できます。

(30 – 平均) / 標準偏差 = (30 – 50) / 10 = -20 / 10 = -2

(70 – 平均) / 標準偏差 = (70 – 50) / 10 = 20 / 10 = 2

値 30 と 70 は、それぞれ平均より下と上の 2 標準偏差です。したがって、 k = 2です。

次に、Excel で次の式を使用して、このデータ セットの平均値の 2 標準偏差以内に収まる値の最小パーセンテージを見つけることができます。

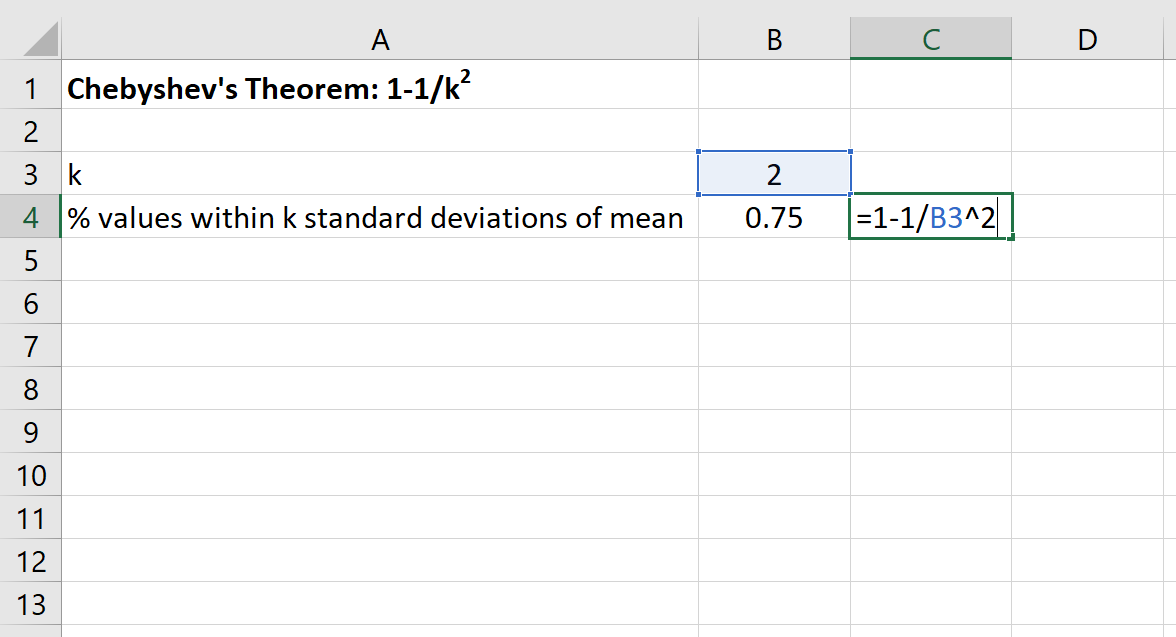
このデータセットの 30 と 70 の間の値の割合は、少なくとも 75%になります。

例 2: チェビシェフの定理を使用して、平均が 35、標準偏差が 5 のデータセットについて、値の何パーセントが 20 ～ 50 の間に入るかを決定します。

まず、k の値を決定します。これは、平均から 20 ～ 50 の間に標準偏差がいくつあるかを決定することで実行できます。

(20 – 平均) / 標準偏差 = (20 – 35) / 5 = -15 / 5 = -3

(50 – 平均) / 標準偏差 = (50 – 35) / 5 = 15 / 5 = 3

値 20 と 50 は、それぞれ平均より 3 標準偏差下と上です。したがって、 k = 3 となります。

次に、Excel で次の式を使用して、このデータ セットの平均値の 3 標準偏差以内に収まる値の最小パーセンテージを見つけることができます。

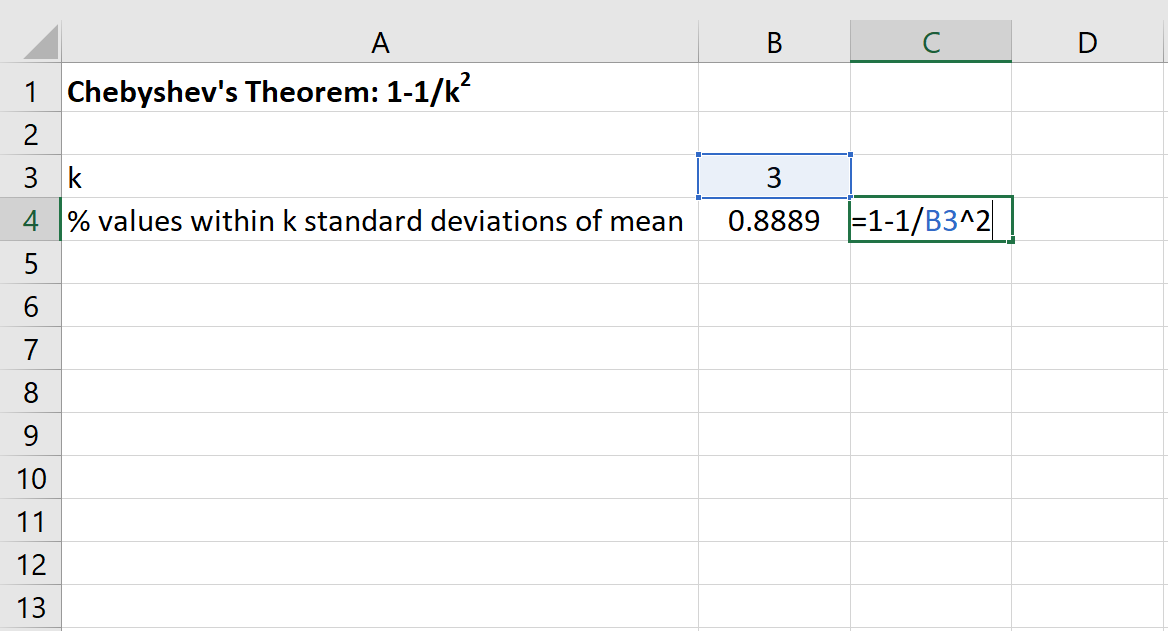
このデータセットの 20 と 50 の間の値の割合は、少なくとも 88.89%になります。

例 3: チェビシェフの定理を使用して、平均 100、標準偏差 5 のデータセットについて、値の何パーセントが 80 ～ 120 の間に入るかを決定します。

まず、k の値を決定します。これは、平均から 80 ～ 120 の間に標準偏差がいくつあるかを決定することで実行できます。

(80 – 平均) / 標準偏差 = (80 – 100) / 5 = -20 / 5 = -4

(120 – 平均) / 標準偏差 = (120 – 100) / 5 = 20 / 5 = 4

値 80 と 120 は、それぞれ平均より下と上の 4 標準偏差です。したがって、 k = 4 となります。

次に、Excel で次の式を使用して、このデータ セットの平均値の 4 標準偏差以内に収まる値の最小パーセンテージを見つけることができます。

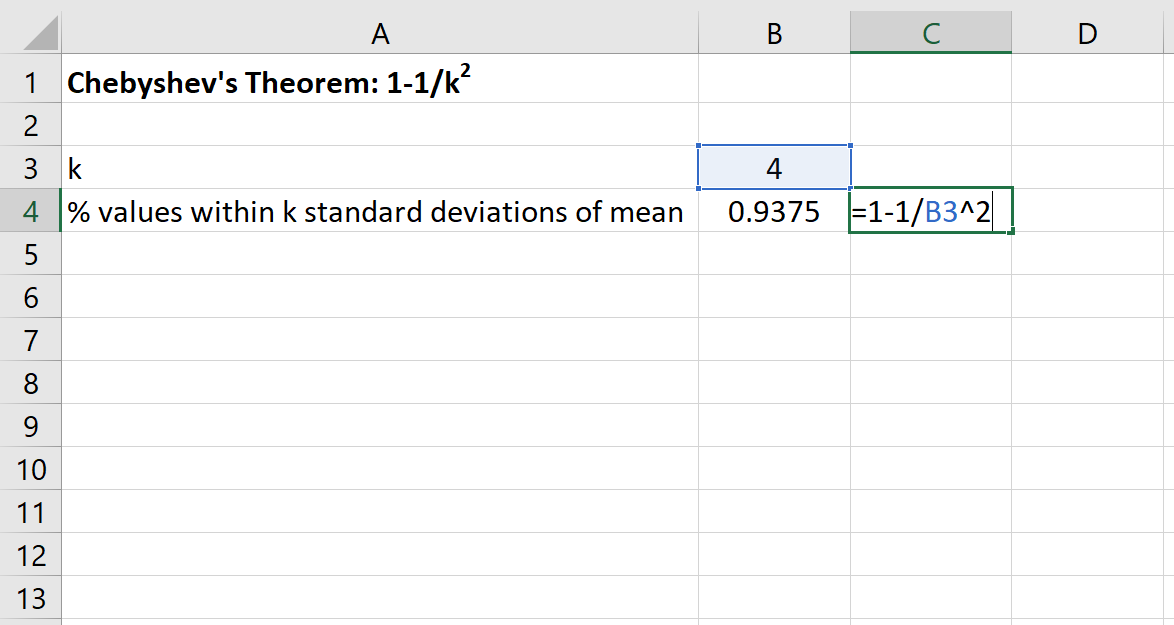
このデータセットの 80 と 120 の間の値の割合は、少なくとも 93.75%になります。