テューキー vs.ボンフェローニ vs.シェッフェ: どのテストを使用する必要がありますか?
一元配置分散分析は、 3 つ以上の独立したグループの平均間に統計的に有意な差があるかどうかを判断するために使用されます。
ANOVA 表全体のp 値が一定の有意性レベルを下回っている場合、グループ平均の少なくとも 1 つが他の平均とは異なると言える十分な証拠があります。
ただし、これではどのグループが互いに異なるかは分かりません。これは単に、すべてのグループの平均が等しいわけではないことを示しています。
どのグループが互いに異なっているかを正確に知るには、 ファミリーごとのエラー率を制御できる事後テストを実行する必要があります。
最も一般的に使用される事後テストには次の 3 つがあります。
- テューキー法
- シェッフェ法
- ボンフェローニ法
このチュートリアルでは、各方法の概要と、状況に応じてどの事後テストを使用するかについて説明します。
テューキー法
Tukey の事後検定は、各グループのサンプル サイズが等しい場合にグループ平均間のペアごとの比較を行う場合に使用する必要があります。
サンプル サイズが等しくない場合は、Tukey-Kramer テストとして知られるテストの修正バージョンを使用できます。
「ペアワイズ」という用語は、一度に 2 つのグループの平均のみを比較したいことを意味します。
たとえば、A、B、C という 3 つのグループがあるとします。
Tukey の事後テストを使用すると、次のペアごとの比較を行うことができます。
- μA = μB
- μA = μC
- μB = μC
k個のグループの場合、合計k ( k -1)/2 個の可能なペアワイズ比較があることに注意してください。
シェッフェ法
シェッフェ事後検定は、グループ平均間の可能な限りの対比を行いたい場合に使用する必要があります。この検定では、Tukey の事後検定とは異なり、一度に 2 つ以上の平均値を比較できます。
たとえば、A、B、C、D という 4 つのグループがあるとします。
シェッフェ事後テストを使用すると、次のような複雑な比較を行うことができます。
- μA – μB = μC – μD
- μA + μD = μB + μC
シェッフェ事後検定は最も柔軟ですが、最も保守的でもあり、最も広い信頼区間を生成します。これは、統計的検出力が最も低く、グループ間の真の差異を検出する能力も最も低いことを意味します。
Scheffe事後検定は、グループのサンプルサイズが等しいかどうかに関係なく使用できることに注意してください。
ボンフェローニ法
Bonferroni 事後テストは、計画された一連の比較を事前に実行する場合に使用する必要があります。
たとえば、A、B、C という 3 つのグループがあり、次の比較のみに関心があることが事前にわかっているとします。
- μA = μB
- μB = μC
このように事前に実行したい特定の比較計画がある場合、ボンフェローニ事後検定は最も狭い信頼区間を生成します。これは、関心のあるグループ間の真の違いを検出する能力が最も高いことを意味します。 。
ボンフェローニ事後検定は、グループのサンプルサイズが等しいかどうかに関係なく使用できることに注意してください。
どの方法を使用する必要がありますか?
次の意思決定ツリーは、状況に応じてどの事後テストを使用するかを決定するのに役立ちます。
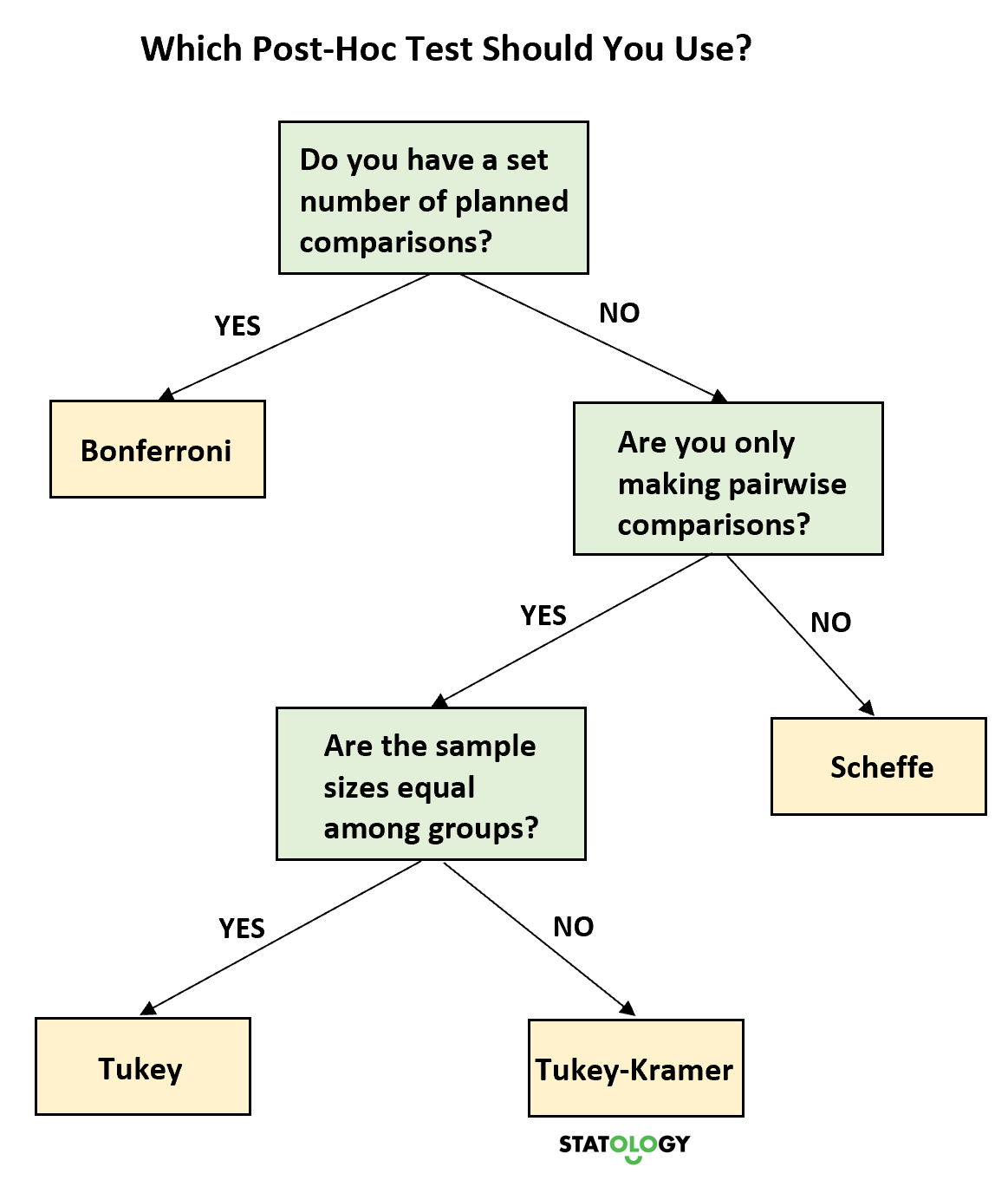
最終的な考え
どちらの事後テストを使用することを選択する場合でも、実験を実行する前に決定する必要があります。
これにより、不正な研究行為とみなされる、重要な結果が得られる可能性が高い実験後の事後テストを選択することができなくなります。
いずれにせよ、ほとんどの統計ソフトウェアはこれらの事後テストを実行できるため、手動で計算する必要はほとんどありません。